المحتويات
مقدمة
بايتورش PyTorch هي مكتبة تعلم الآلة مفتوحة المصدر مبينة على لغة البرمجة بايثون تُستخدم لتطبيقات الرؤية الحاسوبية ومعالجة اللغات الطبيعية، تم تطوير هذه المكتبة من قبل مخبر أبحاث الذكاء الاصطناعي التابع لشركة فيس بوك FAIR، حيث تدعم هذه المكتبة معالجة المصفوفات متعددة الأبعاد Tensor بشكل مشابه لمكتبة بايثون العددية Numpy بالإضافة إلى أداء عالي في المعالجة من خلال الاستفادة من وحدة معالجة الرسوميات GPU.
أساسيات بايتورش
1- إنشاء مصفوفة متعددة الأبعاد
توفر مكتبة بايتورش الصف torch.Tensor والذي يستخدم لتخزين وإجراء العمليات على المصفوفات متعددة الأبعاد، حيث تتشابه المصفوفة متعددة الأبعاد من النوع بايتورش مع المصفوفة من النوع NumPy ولكن يمكن تنفيذ العمليات على المصفوفة من النوع بايتورش في وحدة معالجة الرسوميات وهذا ما يجعل عملية التنفيذ أسرع أما الأخرى Numpy فلا تدعم وحدة معالجة الرسوميات.
دعونا في البداية نلقي نظرة على كيفية إنشاء مصفوفة متعددة الأبعاد باستخدام بايتورش حيث يمكننا إنشاؤها بطريقتين:
الطريقة الأولى – إنشاء المصفوفة وإسناد القيم لها بشكل مباشر، يتم ذلك بالطريقة التالية:
import torch
new_tensor = torch.Tensor([[1, 2], [3, 4]])
بايتورش مبنية على مكتبة torch لذلك تم استدعاء هذه المكتبة في البداية، السطر 1.
الطريقة الثانية – يمكن إنشاء المصفوفة بتعيين أبعادها فقط دون إسناد قيم لها وستأخذ المصفوفة في هذه الحالة قيم عشوائية.
empty_tensor = torch.Tensor(6, 3)

الآن بعد أن تعرفنا على كيفية إنشاء المصفوفة متعددة الأبعاد سنلقي نظرة على كيفية إنشاء أنواع خاصة من المصفوفات.
يمكننا إنشاء مصفوفة متعددة الأبعاد مهيأة بقيم عشوائية بين 1- و1 بالشكل التالي:
uniform_tensor = torch.Tensor(2, 3).uniform_(-1, 1)
لاحظ أن أبعاد المصفوفة السابقة هي 3×2.
يمكننا إنشاء مصفوفة متعددة الأبعاد مهيأة بقيم عشوائية وفق التوزيع المنتظم Uniform distribution على المجال (0,1] بالشكل التالي:
rand_tensor = torch.rand(2, 3)
إنشاء مصفوفة مهيأة بقيم صفرية:
zero_tensor = torch.zeros(2, 3)
نستخدم الفهرسة من أجل الوصول إلى عناصر المصفوفة أو إجراء تعديل عليها، على سبيل المثال [new_tensor [0] [0 تعيد القيمة في الموضع 0،0 كما هو موضح في الشيفرة البرمجية التالية، السطر 8 .
يمكننا أيضا استخدام التابع ()item للوصول إلى القيمة في الموضع 0،0 بالشكل التالي:
new_tensor = torch.Tensor([[1, 2], [3, 4]])
print(new_tensor[0][0])
print(new_tensor[0][0].item())
يتم تعديل القيمة في الموضع 0،0 بالشكل التالي:
new_tensor[0][0] = 5
print(new_tensor)
يمكننا استخدام التشرِيحٌ Slicing للحصول على أي سطر أو عمود من المصفوفة متعددة الأبعاد، على سبيل المثال نستخدم التعليمة التالية للحصول على كل عناصر العمود الأول، السطر 13.
slice_tensor = torch.Tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(slice_tensor[:, 0])
من أجل الحصول على كل عناصر العمود الأخير نستخدم التعليمة التالية:
print(slice_tensor[:, -1])
يتم الحصول على جميع عناصر السطر الثاني بالشكل التالي:
print(slice_tensor[2, :])
جلب جميع العناصر من أول سطرين:
print(slice_tensor[:2, :])
الآن كيف يمكننا الحصول على معلومات حول المصفوفة متعددة الأبعاد ؟؟
نستخدم التابع ()type من أجل معرفة نوع بيانات عناصر المصفوفة.
new_tensor = torch.Tensor([[1, 2], [3, 4]])
print(new_tensor.type())
من أجل معرفة أبعاد المصفوفة نستخدم الخاصيّة shape أو التابع ()size.
print(new_tensor.shape)
print(new_tensor.size())
يتم معرفة بُعد المصفوفة إذا كانت أحادية البُعد أم ثنائية البُعد أم ثلاثية ..الخ باستخدام التابع ()dim.
print(new_tensor.dim())
لإعادة تشكيل المصفوفة reshape نستخدم التابع (view(n,m. وسيؤدي هذا التابع إلى تحويل أبعاد المصفوفة إلى الأبعاد n×m.
reshape_tensor = torch.Tensor([[1, 2], [3, 4]])
reshape_tensor.view(1,4)
reshape_tensor.view(4,1)
2-العمليات على المصفوفات متعددة الأبعاد
يمكن إجراء عملية الجمع بين مصفوفتين بعدة طرق سنتعرف عليها فيما يلي:
الطريقة الأولى – باستخدام معامل الجمع +.
x = torch.rand(5, 3)
y = torch.rand(5, 3)
print(x + y)
الطريقة الثانية – باستخدام التابع torch.add بالشكل التالي:
print(torch.add(x, y))
يمكننا تحديد مصفوفة خرج (الناتج) عملية الجمع بالشكل التالي:
result = torch.empty(5, 3)
torch.add(x, y, out=result)
print(result)
حيث تم جمع المصفوفة x مع المصفوفة y ووضع ناتج عملية الجمع في المصفوفة result.
بنفس الشكل يتم تطبيق بقية العمليات الرياضية على المصفوفات، فمن أجل الضرب العددي Scalar Multiplication نستخدم التابع (torch.mul(x,y أما بالنسبة لعملية الطرح نستخدم التابع (torch.sub(x,y وبالنسبة لعملية القسمة نستخدم (torch.div(x,y.
الآن لإيجاد منقول مصفوفة Transpose نستخدم التابع ()t. أو (permute(-1,0.
my_tensor = torch.rand(5, 3)
my_tensor.t()
my_tensor.permute(-1,0)
يستخدم التابع ()mm. من أجل تنفيذ الضرب المصفوفي Matrix Multiplication.
tensor_1 = torch.randn(3, 3)
tensor_2 = torch.randn(3, 3)
maxtrix_prod = tensor_1.mm(tensor_2)
توضيح: تختلف عملية الضرب العددي عن عملية الضرب المصفوفي، فالأولى (الضرب العددي) تتم بين مصفوفة وعدد ويتم ضرب هذا العدد بجميع عناصر المصفوفة أما بالنسبة للعملية الثانية فتتم بين مصفوفتين ويجب أن يكون عدد أعمدة المصفوفة الأولى مساوية لعدد أسطر المصفوفة الثانية.
تمكننا مكتبة بايتورش من نقل جميع العمليات إلى وحدة معالجة الرسوميات GPU لكن هذا الأمر يتطلب توافر معالج رسوميات NVIDIA، حيث يمكننا نقل العمليات إلى وحدة معالجة الرسوميات باستخدام التابع to. بالشكل التالي:
x = torch.randn(4, 4)
y = torch.randn(4, 4)
if torch.cuda.is_available():
device = torch.device("cuda")
x = x.to(device)
y = y.to(device)
z = x + y
print(z)
قبل نقل العمليات إلى وحدة معالجة الرسوميات نتحقق إذا كانت منصة كودا CUDA متاحة أم لا، السطر40.
ملاحظة : كودا CUDA اختصار لـ Compute Unified Device Architecture وهي منصة حوسبة تفرعية ونموذج برمجي يمكننا من الوصول إلى وحدة معالجة الرسوميات.
في بعض الأحيان نحتاج إلى تحويل المصفوفة من النوع Numpy إلى مصفوفة بايتورش والعكس، نستخدم التابع ()from_numpy عند التحويل من مصفوفة Numpy إلى مصفوفة بايتورش.
import numpy as np
np_ndarray = np.random.randn(2,2)
to_tensor = torch.from_numpy(np_ndarray)
ونستخدم التابع ()numpy لتحويل إلى مصفوفة Numpy.
to_ndarray = to_tensor.numpy()
بناء شبكة عصبونية باستخدام بايتورش
سنقوم ببناء نموذج يقوم بالتنبُّؤ بطقس الغد فيما إذا كان ماطراً أم لا وذلك عن طريق تدريب شبكة عصبونية على مجموعة بيانات تحتوي على معلومات حول الطقس، هذه المعلومات تم تسجيلها بشكل يومي بواسطة محطات طقس استرالية عديدة على مدار 10 سنوات وهذه معلومات تتضمن معدل الرطوبة، سرعة الرياح، الضغط الجوي …(يمكننا تحميل مجموعة البيانات من موقع كاغل Kaggle من رابط هنا).
سنتعلم كيفية:
- معالجة ملفات CSV وكيفية تحويل البيانات إلى مصفوفات متعددة الأبعاد من النوع بايتورش.
- بناء شبكة عصبونية باستخدام بايتورش.
- استخدام تابع الخسارة Loss Function والمحسّن Optimizer في تدريب الشبكة العصبونية.
- تقييم أداء النموذج بعد الانتهاء من عملية التدريب.
يمكنك عزيزي القارئ الاطلاع على كامل الشيفرة البرمجية من خلال زيارة الرابط التالي
في البداية نقوم باستدعاء المكتبات التي سنتعامل معها وتهيئة بعض المتحولات الضرورية:
import torch
import os
import numpy as np
import pandas as pd
from tqdm import tqdm
import seaborn as sns
from pylab import rcParams
import matplotlib.pyplot as plt
from matplotlib import rc
%matplotlib inline
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, classification_report
from torch import nn, optim
import torch.nn.functional as F
RANDOM_SEED = 42
np.random.seed(RANDOM_SEED)
torch.manual_seed(RANDOM_SEED)
نقوم بتحميل مجموعة البيانات باستخدام مكتبة بانداس Pandas.
df = pd.read_csv('weatherAUS.csv')

نلاحظ بالنظر إلى الشكل 2 أن مجموعة البيانات لدبنا تحتوي على عدد كبير من الميزات feature (أعمدة). من أجل تبسيط الأمر أكثر سنقوم باستخدام 4 ميزات فقط في عملية التدريب، حيث سنختار ميزة معدل هطول الأمطار Rainfall والضغط 9 مساءً Pressure9am والرطوبة 3 صباحاً Humidity3pm وحالة الطقس اليوم RainToday ولا ننسى أننا سنعتمد حالة الطقس غداً RainTomorrow كقيمة للخرج.
cols = ['Rainfall', 'Humidity3pm', 'Pressure9am', 'RainToday', 'RainTomorrow']
df = df[cols]
الشبكة العصبونية تفهم لغة الأرقام فقط وغير قادرة على التعامل مع السلاسل النصية، فالعمودين RainToday و RainTomorrow الموجودين في مجموعة البيانات يحتويان على الكلمات النصية Yes و No لذلك لابد من إجراء عملية معالجة على هذين العمودين وتحويل هاتين الكلمتين إلى قيم رقمية مقابلة حيث نقوم بتحويل الكلمة No إلى القيمة الرقمية 0 وأيضاً الكلمة Yes إلى القيمة 1 بالشكل التالي:
df['RainToday'].replace({'No': 0, 'Yes': 1}, inplace = True)
df['RainTomorrow'].replace({'No': 0, 'Yes': 1}, inplace = True)
دعنا نقوم أيضاً بإجراء عملية معالجة على كامل مجموعة البيانات حيث نقوم بحذف الأسطر في حال حوت على قيمة غير محددة NaN.
df = df.dropna(how='any')
أحد أهم الأمور التي يجب النظر إليها هي مدى توازن مجموعة البيانات لدينا أي كم عدد العينات الموجودة في مجموعة البيانات الخاصة بالصنف “ماطر غداً” و الصنف “غير ماطر غداً”. باستخدام التعليمة التالية سنقوم برسم مخطط بياني يوضح ذلك.
sns.countplot(df.RainTomorrow)
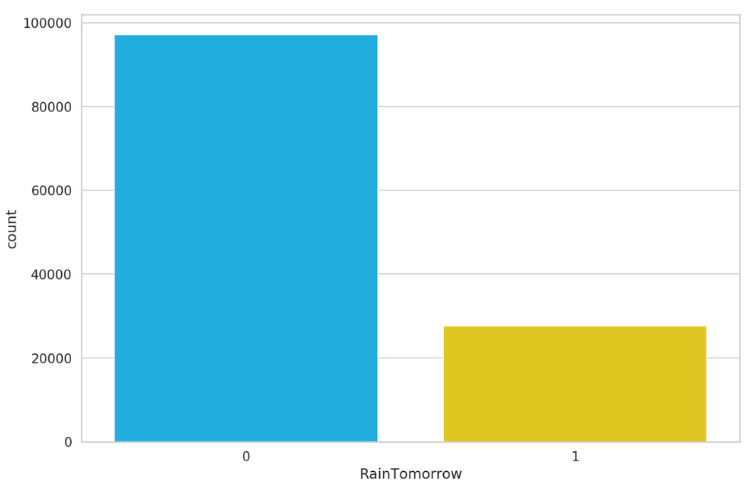
بالنظر إلى النتيجة السابقة (الشكل 3) نلاحظ أن مجموعة البيانات لدينا غير متوازنة imbalance أي أن عدد عينات الصنف “غير ماطر غداً” أكبر بكثير من عدد عينات الصنف “ماطر غداً” وهي حالة غير جيدة لأنه في هذه الحالة ستتدرب الشبكة العصبونية على الصنف “غير ماطر غداً” بشكل جيد وبشكل أفضل من الصنف “ماطر غداً”.
الآن نقوم بتقسيم مجموعة البيانات لدينا إلى مجموعة بيانات تدريب ومجموعة بيانات اختبار.
X = df[['Rainfall', 'Humidity3pm', 'RainToday', 'Pressure9am']]
y = df[['RainTomorrow']]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=RANDOM_SEED)
نقوم بتحويل بيانات التدريب والاختبار إلى مصفوفات متعددة الأبعاد من النوع بايتورش حتى نتمكن من إجراء العمليات عليها واستخدامها في تدريب واختبار الشبكة العصبونية باستخدام مكتبة بايتورش.
X_train = torch.from_numpy(X_train.to_numpy()).float()
y_train = torch.squeeze(torch.from_numpy(y_train.to_numpy()).float())
X_test = torch.from_numpy(X_test.to_numpy()).float()
y_test = torch.squeeze(torch.from_numpy(y_test.to_numpy()).float())
ملاحظة : التابع torch.squeeze يقوم بإرجاع مصفوفة متعددة الأبعاد مع إزالة جميع الأبعاد التي بالحجم 1، على سبيل المثال إذا كانت أبعاد الدخل A×1×B×C بالتالي تكون أبعاد مصفوفة الخرج A×B×C.
عزيزي القارئ في حال أردت معرفة تفاصيل أكثر حول التابع torch.squeeze يمكنك الانتقال إلى الموقع هنا.
الآن سنقوم ببناء شبكة العصبونية تأخذ البيانات التالية كمُدخلات لها:
- معدل هطول الأمطار.
- الضغط 9 مساءً.
- الرطوبة 3 صباحاً.
- حالة الطقس اليوم.
سننشئ طبقة دخل مناسبة لهذه البيانات.
بالنسبة للخرج سيكون بين 0 و 1 ويمثل احتمالية هطول الأمطار في الغد، وسننشئ أيضاُ طبقة خرج مناسبة لذلك.
سنضيف طبقتين مخفيتين بين طبقة الدخل والخرج حيث تحدد عصبونات هاتين الطبقتين الخرج النهائي للشبكة العصبونية.
ستكون جميع الطبقات متصلة بالكامل fully-connected.
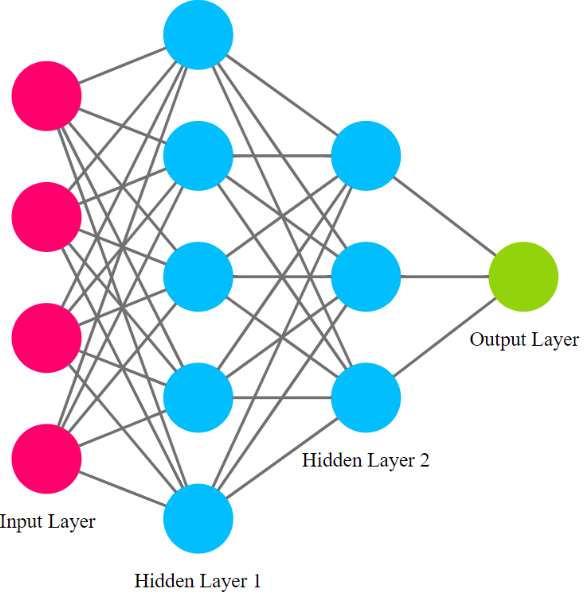
تمتلك مكتبة بايتورش أسلوباً محدداً في بناء الشبكة العصبونية حيث يتم إنشاء صف Class يتم فيه تحديد معمارية الشبكة العصبونية (الطبقات، توابع التفعيل، طريقة الأتصال بين الطبقات … ) وهذا الصف يجب أن يرث الصف nn.Module بالشكل التالي:
class Net(nn.Module):
def __init__(self, n_features):
super(Net, self).__init__()
self.fc1 = nn.Linear(n_features, 5)
self.fc2 = nn.Linear(5, 3)
self.fc3 = nn.Linear(3, 1)
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
return torch.sigmoid(self.fc3(x))
net = Net(X_train.shape[1])
نلاحظ أنه يتم تعريف طريقتين فقط داخل الصف Net، الطريقة الأولى وهي الباني –init– والطريقة الثانية هي التمرير للأمام forward.
بالنسبة للطريقة الأولى (الباني) كما الحال في صفوف بايثون يتم تعريف خصائص الصف attribute داخل هذه الطريقة وفي حالتنا هنا نستخدم هذه الطريقة من أجل تحديد طبقات الشبكة العصبونية.
التابع super يوفر لنا إمكانية الوصول إلى طرائق الصف الأب الذي ورثناه أي nn.Module.
لاحظ في السطر37 قمنا بإنشاء أول طبقة مخفية التي تقبل الميزات الأربع /4/ كدخل و لها 5 مخرجات حيث سيتم تلقائياً إنشاء مصفوفة أوزان وانحياز خاصة بهذه الطبقة، يمكننا الوصول إلى مصفوفة الأوزان باستخدام net.fc1.weight والانحياز باستخدام net.fc1.bais.
الطريقة الثانية وهي طريقة التمرير للأمام في هذه الطريقة نحدد كيفية اتصال الطبقات ببعضها البعض ويتم فيها أيضاً تحديد توابع التفعيل التي ستطبق على خرج الطبقات (لا ننسى أن الطبقات تم تحديدها داخل الباني)، وأخيراً تقوم هذه الطريقة بإرجاع خرج الشبكة.
لاحظ في السطر41 نقوم بتطبيق تابع وحدةُ التَّصحيحِ الخطِّيِّ Relu على خرج الطبقة الأولى أي
( self.fc1 = nn.Linear(n_features, 5 .
في السطر44 قمنا بأخذ غرض من صف الشبكة العصبونية.
الآن نختار تابع الخسارة المناسب لمشكلة التصنيف الثنائي Binary Classification وسنختار تابع الإنتروبيا المُتقاطِعةُ الثُّنائيَّةُ Binary Cross-Entropy الذي يقيس الفرق بين تنبؤات النموذج والقيمة الحقيقة وكلما اقتربت قيمة هذا التابع من الصفر كلما كان أداء النموذج أفضل.
criterion = nn.BCELoss()
لكن كيف نستطيع الوصول إلى الأوزان التي تحقق أقل قيمة لتابع الخسارة وتجعله قريب جداً من الصفر؟؟
يتم ذلك بواسطة المُحسّن الذي يعمل على تعديل الأوزان باستمرار حتى يتقارب تابع الخسارة من الصفر.
هناك الكثير من المُحسّنات التي يمكن اختيارها إلا أننا سنقوم بإختيار محسن آدم Adam.
optimizer = optim.Adam(net.parameters(), lr=0.001)
يتطلب المُحسّن أن نمرر له أوزان الشبكة العصبونية وكذلك قيمة معدّل التعلم Learning Rate.
الآن نتحقق إذا كانت منصة كودا CUDA متاحة أم لا، في حال كانت متاحة نقوم بنقل جميع بيانات التدريب والاختبار إليها وأيضاً نقوم بنقل النموذج وتابع الخسارة.
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
X_train = X_train.to(device)
y_train = y_train.to(device)
X_test = X_test.to(device)
y_test = y_test.to(device)
net = net.to(device)
criterion = criterion.to(device)
نُعرّف تابع لحساب دقة النموذج Accuracy وذلك من أجل تتبع دقة النموذج أثناء عملية التدريب.
def calculate_accuracy(y_true, y_pred):
predicted = y_pred.ge(.5).view(-1)
return (y_true == predicted).sum().float() / len(y_true)
يمكننا الآن بدء تدريب النموذج حيث نقوم بتحديد 1000 دورة تدريب وعند كل 100 دورة سنقوم بعرض الدقة والخسارة لكل من بيانات التدريب والاختبار.
في كل دورة تدريب نقوم بـ:
- حساب تابع الخسارة وحذف الاشتقاقات المتراكمة باستخدام التابع ()zero_grad.
- حساب مشتق تابع الخسارة بالنسبة للمعاملات (الانتشار الخلفي) يتم ذلك باستخدام التابع ()backward.
- القيام بخطوة محسن لتحديث أوزان الشبكة العصبونية.
def round_tensor(t, decimal_places=3):
return round(t.item(), decimal_places)
for epoch in range(1000):
y_pred = net(X_train)
y_pred = torch.squeeze(y_pred)
train_loss = criterion(y_pred, y_train)
if epoch % 100 == 0:
train_acc = calculate_accuracy(y_train, y_pred)
y_test_pred = net(X_test)
y_test_pred = torch.squeeze(y_test_pred)
test_loss = criterion(y_test_pred, y_test)
test_acc = calculate_accuracy(y_test, y_test_pred)
print(
f'''epoch {epoch}
Train set - loss: {round_tensor(train_loss)}, accuracy: {round_tensor(train_acc)}
Test set - loss: {round_tensor(test_loss)}, accuracy: {round_tensor(test_acc)}
''')
optimizer.zero_grad()
train_loss.backward()
optimizer.step()
توضيح حول عمل التابع zero_grad:
في كل دورة تدريب قبل إجراء الانتشار الخلفي نحتاج إلى حذف اشتقاقات الدورة السابقة وإلا سيقوم بايتورش بجمع اشتقاقات الدورة الحالية مع اشتقاقات الدورات السابقة بشكل تراكمي (أي جميع الاشتقاقات التي تم إيجادها عند كل استدعاء لتابع الانتشار الخلفي backward) وعندها لن يتم التقارب من الحل الأمثل الذي يحقق أقل قيمة لتابع الخسارة، لذلك لابد من حذف الاشتقاقات المتراكمة عند كل دورة تدريب باستخدام التابع ()zero_grad.
في بعض الأحيان قد يستغرق التدريب الجيد للنموذج أسابيع وربما أشهر لذلك لابد من حفظ النموذج بعد الانتهاء من تدريبه حتى نتمكن من إعادة استخدامه لاحقاً دون الحاجة إلى التدريب مرة أخرى.
يمكننا حفظ النموذج باستخدام التعليمة التالية:
MODEL_PATH = 'model.pth'
torch.save(net, MODEL_PATH)
يمكننا استعادة النموذج الذي قمنا بحفظه باستخدام التعليمة التالية:
net = torch.load(MODEL_PATH)
استخدام مقياس الدقة فقط من أجل قياس أداء النموذج غير كافي وخاصة في حال كانت مجموعة البيانات غير متوازنة ومن الأفضل استخدام طرق أخرى إضافية لقياس أداء النموذج سنتعرف عليها.
إحدى الطرق الإضافية لقياس أداء النموذج تتمثل بحساب قيمة التنبؤ الإيجابي Precision وحساسية التنبؤ Recall من أجل كل صنف من أصناف الخرج وفي حالتنا هنا سنقوم بحساب قيمة التنبؤ الإيجابي وحساسية التنبؤ من أجل كلاً من الصنفين ماطر غدا و غير ماطر.
classes = ['No rain', 'Raining']
y_pred = net(X_test)
y_pred = y_pred.ge(.5).view(-1).cpu()
y_test = y_test.cpu()
print(classification_report(y_test, y_pred, target_names=classes))
قيمة التنبؤ الإيجابي تتراوح بين 0 و1 وكلما اقتربت قيمة التنبؤ الإيجابي من الواحد كلما كان أداء النموذج أفضل في توقع الصنف.
وكذلك أيضاً حساسية التنبؤ تترواح بين 0 و1 وكلما اقتربت من الواحد تشير إلى قدرة النموذج على اكتشاف الصنف أكثر.
سنقوم بتوضيح العلاقة الرياضية لكلاً من قيمة التنبؤ الإيجابي و حساسية التنبؤ في نهاية المقال.
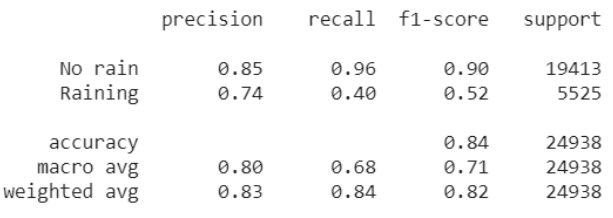
بالنظر إلى الشكل 5 عند قيمتي التنبؤ الإيجابي و حساسية التنبؤ نلاحظ أن النموذج يتنبأ بشكل أفضل عندما يتعلق الأمر بالصنف “غير ماطر”، ولا يتنبأ بشكل جيد عندما يتعلق الامر بالصنف “ماطر” وهذا يعني أننا لا نثق في تنبؤات النموذج عندما يتنبأ بأنها ستمطر غداً.
يمكننا أيضاً التعمق في قياس أداء النموذج عن طريق إيجاد مصفوفة الالتباس confusion matrix التي تمكننا من معرفة جميع الأخطاء التي ارتكبها النموذج في عملية التنبؤ.
cm = confusion_matrix(y_test, y_pred)
df_cm = pd.DataFrame(cm, index=classes, columns=classes)
hmap = sns.heatmap(df_cm, annot=True, fmt="d")
hmap.yaxis.set_ticklabels(hmap.yaxis.get_ticklabels(), rotation=0, ha='right')
hmap.xaxis.set_ticklabels(hmap.xaxis.get_ticklabels(), rotation=30, ha='right')
plt.ylabel('True label')
plt.xlabel('Predicted label');
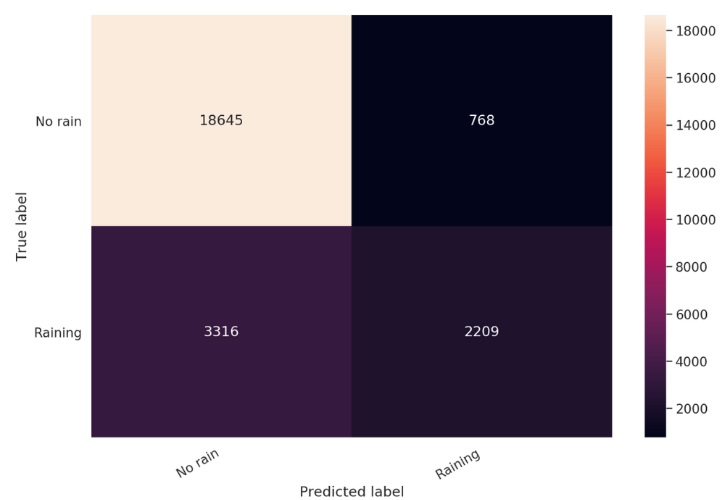
دعونا الآن نوضح ماهي مصفوفة الالتباس وإلى ماذا تشير الأرقام بداخلها.
مصفوفة الالتباس: هي جدول يستخدم لوصف أداء النموذج على مجموعة بيانات الاختبار.

نلاحظ من الشكل 7 أن الأعمدة تمثل الفئات المتنبئة Predicted بينما الأسطر تمثل الفئات الحقيقة Actual.
عزيزي القارئ عند قراءتك للمصطلحات التالية عليك النظر باستمرار إلى الشكل 7 لتتضح الأمور بالنسبة لك اكثر:
- TP: هي اختصار لـ True Positive وهي قيمة التنبؤ الإيجابي الصحيح، مثلاً غداً ماطر والنموذج تنبأ بذلك.
- FP: هي اختصار لـ False Positive وهي قيمة التنبؤ الإيجابي الخاطئ، مثلاً غداً غير ماطر والنموذج تنبأ بأنه ماطر.
- TN: هي اختصار لـ True Negative وهي قيمة التنبُّؤ السلبي الصحيح، مثلاً غداً غير ماطر والنموذج تنبأ بذلك.
- FN: هي اختصار لـ False Negative وهي قيمة التنبُّؤ السلبي الخاطئ، مثلاً غداً ماطر والنموذج تنبأ بأنه غير ماطر.
بالنسبة لقيمة التنبؤ الإيجابي وحساسية التنبؤ سنقوم بتوضيح العلاقة الرياضبة لهما:
أولاً – قيمة التنبؤ الإيجابي تجيب على السؤال التالي:
عندما تنبأ النموذج بنعم، كم مرة كان التنبؤ صحيح ؟
وتعطى قيمة التنبؤ الإيجابي بالعلاقة الرياضية التالية:
(Precision = TP / (TP+FP
ثانياً – حساسية التنبؤ تجيب على السؤال التالي:
ماهي نسبة اكتشاف النموذج للصنف الإيجابي (الصنف المرتبط).
وتعطى قيمة حساسية التنبؤ بالعلاقة الرياضية التالية:
(Recall = TP / (TP+FN
الخاتمة
تعرفنا في هذا المقال على كيفية إنشاء مصفوفة متعددة الأبعاد باستخدام مكتبة بايتورش ووضحنا بعض العمليات على المصفوفات متعددة الأبعاد من النوع بايتورش وتعلمنا كيفية بناء شبكة عصبونية وتدريبها باستخدام مكتبة بايتورش، وأخيراً رأينا كيف يتم قياس أداء النموذج المُدرّب.


تعليق واحد
أبدعت شكرا لك