التدّقيق العلمي: د. م. حسن قزّاز، م. محمد سرميني
التدّقيق اللّغوي: هبة الله فلّاحة
المحتويات
- مقدّمة:
- تعريف السّلسلة الزّمنيّة ومكوناتها:
- التنبّؤ بالسّلاسل الزّمنيّة:
- أنواع بيانات التنبّؤ بالسّلاسل الزّمنيّة:
- توقّعات أحاديّة المتغيّر Univariate Forecast:
- التنبّؤ متعدّد المتغيّرات Multivariate Forecast:
- طرق التنبّؤ بالسّلاسل الزّمنية:
- النّماذج الإحصائيّة Statistical Models:
- نماذج التّعلّم الآليّ Machine Learning والتّعلّم العميق Deep Learning
- التنبّؤ بالسّلاسل الزّمنيّة متعدّدة المتغيّرات Multivariate باستخدام الشّبكة العصبونيّة ذات الذّاكرة الطّويلة قصيرة المدى LSTM:
- الخاتمة:
- المراجع:
مقدّمة:
التنبّؤ بالسّلاسل الزّمنيّة Time Series forecasting يتمّ من خلال استخدام نماذج إحصائيّة أو نماذج تعتمد على تقنيّات الذّكاء الاصطناعيّ؛ للتنبّؤ بالقيم المستقبليّة لسلسلة زمنيّة محدّدة بناءً على قيمها السّابقة، تُستخدم بيانات السّلاسل الزّمنيّة في مجموعة واسعة من المجالات مثل الماليّة والاقتصاد والأرصاد الجويّة، حيث يقوم النّموذج بتحليل تسلسل القيم السّابقة وتحديد ميزات تساعد في تحديد القيم المستقبليّة، في هذا المقال سنتعرّف على أنواع السّلاسل الزّمنية والطّرق المتّبعة للتنبّؤ بها، وسيتمّ شرح مثال عمليّ لتحليل أسعار مبيعات شركة غوغل Google بالدّولار الأمريكيّ خلال فترة زمنيّة والتنبّؤ بحركة السّهم في المستقبل.
تعريف السّلسلة الزّمنيّة ومكوناتها:
السّلسلة الزّمنيّة هي سلسلة من نقاط البيانات المفهرسة (الرّسوم البيانيّة) المعتمدة على ترتيب زمنيّ معيّن، أي أنّها تسلسل مأخوذ في نقاط زمنيّة متعاقبة متساوية، بحيث يكون الهدف من دراستها وتحليلها هو التنبّؤ بالقيم المستقبليّة ويوضّح الشّكل (1) مثالًا عن السّعر اليوميّ للسّهم وهو مثال عن السّلاسل الزّمنيّة [1].

يمكن تحليل السٌلاسل الزّمنيّة إلى أربعة مكوّنات أساسيّة؛ وهي الاتّجاه trend والموسميّة seasonality والدّوريّة Cyclicity والضّجيج noise موضّحة بالشّكل (2).
- الاتّجاه trend: ويعبّر عن اتّجاه حركة البيانات مع الزّمن، يمكن أن يكون الاتّجاه تصاعديًّا أو تنازليًّا أو مسطّحًا.
- الموسميّة seasonality: أنماط منتظمة تتكرّر بمرور الوقت مثل الأنماط الشّهريّة أو السّنوية، تستخدم لتسليط الضّوء على النّمط المتكرّر للسّلوك بمرور الوقت.
- الدّوريّة Cyclicity: لتحديد التّغييرات المتكرّرة في السّلسلة الزّمنيّة، وتحديد موضعها في الدّورة.
- الضّجيج noise: الاختلافات العشوائيّة في البيانات التي لا يمكن تفسيرها بالاتّجاه أو الموسميّة [1].

التنبّؤ بالسّلاسل الزّمنيّة:
هو عمليّة تحليل بيانات السّلاسل الزّمنيّة باستخدام القواعد الإحصائيّة والنّمذجة لتوقّع الأحداث المحتمل وقوعها، قد لا يكون التنبّؤ دقيقًا دائمًا ويمكن أن تختلف احتماليّة التنبّؤات بشكل كبير؛ خاصّة عند التّعامل مع المتغيّرات المتقلّبة في بيانات السّلاسل الزّمنيّة، لكن كلّما كانت البيانات المتوفّرة لدينا أكثر شمولًا زادت دقّة التّوقّعات، وقد يشير التنبّؤ إلى البيانات في نقطة مستقبليّة محدّدة، ويمكن أن يشير إلى البيانات المستقبليّة بشكل عام، وغالبًا ما يتمّ استخدام التنبّؤ المتسلسل مع تحليل السّلاسل الزّمنيّة. يتضمّن تحليل السّلاسل الزّمنيّة تطوير نماذج لفهم البيانات ومعرفة أسبابها، ثمّ يأخذ التنبّؤ الخطوة التّالية لما يجب فعله بهذه المعرفة والاستقراء المتوقّع لما قد يحدث في المستقبل [3].
أنواع بيانات التنبّؤ بالسّلاسل الزّمنيّة:
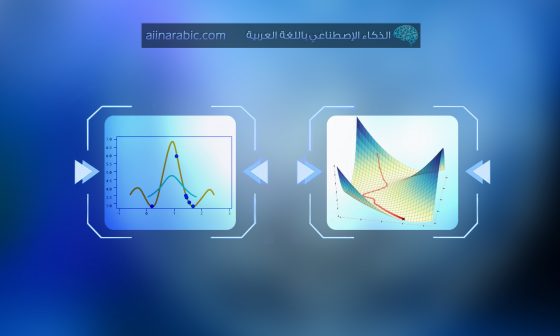
يوجد نوعان من أنواع البيانات؛ بيانات أحاديّة المتغيّر Univariate يعتمد الخرج على متغيّر وحيد وهو متغيّر الدّخل، وبيانات متعدّدة المتغيّرات Multivariate يتعلّق الخرج بعدّة متغيّرات للدّخل ويوضّح الشّكل (3) علاقة الخرج بالدّخل في كلا النّوعين.

توقّعات أحاديّة المتغيّر Univariate Forecast:
السّلسلة الزّمنية أحاديّة المتغيّر هي سلسلة ذات متغيّر واحد يعتمد على الزّمن فقط، وكمثال عليها في حال كنّا نقوم بتتبّع قيم درجة الحرارة بالسّاعة لمنطقة معيّنة ونرغب بالتنبّؤ بدرجة الحرارة المستقبليّة باستخدام درجات الحرارة السّابقة، فهذا هو التنبّؤ بسلسلة زمنيّة أحاديّة المتغيّر. وتكون بياناتها على النّحو التالي الموضّح في الجدول (1):
الجدول (1): مثال عن سلسلة زمنيّة أحاديّة المتغيّر [4].

التنبّؤ متعدّد المتغيّرات Multivariate Forecast:
تحتوي السّلسلة الزّمنية متعدّدة المتغيّرات على أكثر من متغيّر واحد يعتمد على الوقت.
بالتّركيز على المثال السّابق نفترض أنّ مجموعة البيانات الخاصّة بنا تتضمّن ميزات أخرى متعلّقة بالطّقس خلال نفس الفترة الزّمنيّة، مثل الرّطوبة وسرعة الرّياح وما إلى ذلك مع قيم درجة الحرارة، في هذه الحالة هناك العديد من المتغيّرات التي يجب مراعاتها للتنبّؤ بدرجة الحرارة على النّحو الأمثل، عندها سلسلة البيانات هذه تندرج تحت فئة السّلاسل الزّمنية متعدّدة المتغيّرات، وتكون مجموعة البيانات على النّحو التّالي الموضّح بالجدول (2):
الجدول (2): مثال عن سلسلة زمنيّة متعدّدة المتغيّرات [4].

عندما نتعامل مع تنبّؤ السّلاسل الزّمنية متعدّدة المتغيّرات، يمكن أن تكون متغيّرات الدّخل من نوعين:
- خارجيّة: متغيّرات الدّخل لاتتأثر بمتغيّرات الدّخل الأخرى والتي يعتمد عليها متغيّر الخرج.
- داخليّة: متغيّرات الدّخل التي تتأثّر بمتغيّرات الدّخل الأخرى والتي يعتمد عليها متغيّر الخرج [4].
طرق التنبّؤ بالسّلاسل الزّمنية:
يمكن تصنيف التنبّؤ بالسّلسلة الزّمنية إلى الفئات التّالية:
- النّماذج الكلاسيكيّة / الإحصائيّة.
- نماذج التّعلّم الآليّ Machine Learning والتّعلّم العميق Deep Learning.
النّماذج الإحصائيّة Statistical Models:
هناك عدد كبير من الخوارزميّات الشّائعة والمقبولة التي تعتمد على النّماذج الإحصائيّة في تنبّؤ السّلاسل الزّمنيّة والتي تعتمد على طرائق رياضيّة مختلفة.
- نماذج الانحدار التّلقائيّ Autoregressive(AR: تفترض هذه النّماذج أنّ القيمة المستقبليّة لسلسلة زمنيّة تكون تابعًا خطّيًّا.
- نماذج متوسّط التّحرّك Moving average(MA: تفترض هذه النّماذج أنّ القيمة المستقبليّة للسّلسلة الزّمنية هي دالة خطّيّة للخطأ (أي الفرق بين القيمة الفعليّة والقيمة المتوقّعة).
- نماذج الانحدار التّلقائيّ لمتوسّط التّحرّك (ARMA) Autoregressive moving average: تجمع هذه النّماذج بين نماذج الانحدار التّلقائيّ ومتوسّط التّحرّك، وتستخدم عندما يكون كلّ من الاتّجاه والموسميّة لسلسلة زمنيّة خطّيّة.
- نماذج متوسّط التّحرّك المتكامل للانحدار التّلقائيّ autoregressive integrated moving average (ARIMA: تُستخدم هذه النّماذج عندما لا يكون الاتّجاه والموسميّة لسلسلة زمنيّة خطّيّين.
- التّحليل الموسميّ Seasonal decomposition: هذا أسلوب لفصل مكوّنات الاتّجاه والموسميّة والضّجيج في سلسلة زمنيّة [1].
نماذج التّعلّم الآليّ Machine Learning والتّعلّم العميق Deep Learning
هناك العديد من التّقنيّات المستخدمة في التنبّؤ بالسّلاسل الزّمنيّة التي تحاول تحقيق الدّقّة وتقليل الأخطاء والخسائر ومن أهمّ هذه التّقنيّات [2]:
- شبكة بيرسبترون متعدّدة الطّبقات Multi-Layer Perceptron.
-
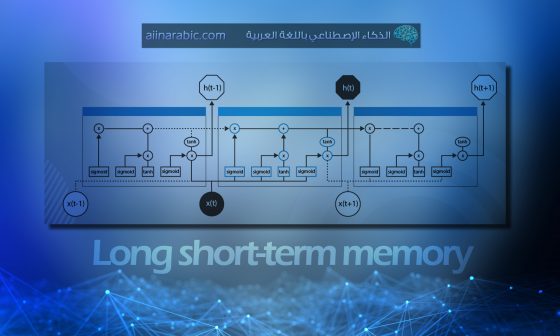
الشّبكة العصبيّة الإرجاعيّة (RNN): تكمن أهمّيّة الشّبكات العصبيّة الإرجاعيّة RNN، في احتوائها على ذاكرةٍ تجعل منها أداةً فعّالة في توقّع الأحداث المتتالية، ممّا يساعدها على توقّع الأحداث ضمن السّلاسل الزّمنيّة. ومن أهمّ إصداراتها الشّبكة العصبونيّة ذات الذّاكرة الطّويلة قصيرة المدى LSTM حيث تعدّ من أقوى الأدوات المستخدمة في مجال الذّكاء الاصطناعيّ وتعلّم الآلة، فهي قادرة على التّعلّم وتصنيفِ الأنماط بكفاءةٍ عالية، كما أنّها تتحلّى بقدرٍ عالٍ من الدّيناميكيّة [5].
- النّماذج القائمة على شجرة القرار مثل Random Forest: شجرة القرار هي شجرة ثنائيّة (binary tree) وهذا يعني أنّ لكلّ أب ولدين على الأكثر، كلّ عقدة (node) في الشّجرة تمثّل متغيّرًا (variable) بينما أوراق الشّجرة (leaf nodes) تمثّل النّتيجة (output) التي تستخدم للتنبّؤ.
- إطار تعزيز التّدرّج الخفيف (Light Gradient-Boosting Machine(LightGBM: هو نوع آخر من خوارزميّات التّعزيز التي أظهرت أنّها أسرع وأحيانًا أكثر دقّة من خوارزميّة تعزيز التّدرّج الشّديد XGBoost، ما يجعل LightGBM مختلفًا هو أنّه يستخدم تقنيّة فريدة تسمّى أخذ العيّنات من جانب واحد قائم على التّدرّج.
- مكتبة تعزيز التّدرّج الشّديد XGBoost) eXtreme Gradient Boosting): هي واحدة من خوارزميّات التّعزيز الشّائعة بشكل كبير والمستخدمة على نطاق واسع لأنّها ببساطة قوية جدًّا، وتعتبر مشابهة لخوارزميّة التّعزيز الاشتقاقيّ Gradient Boost لكنّها تحتوي على بعض الميزات الإضافيّة التي تجعلها أقوى بكثير؛ حيث التّدريب سريع جدًّا ويمكن موازنته أو توزيعه عبر المجموعات [6].
التنبّؤ بالسّلاسل الزّمنيّة متعدّدة المتغيّرات Multivariate باستخدام الشّبكة العصبونيّة ذات الذّاكرة الطّويلة قصيرة المدى LSTM:
فيما يأتي تطبيق عمليّ للتّعرّف على السّلاسل الزّمنيّة باستخدام الشّبكات العُصبُونِيَّة الإرجاعِيَّة RNN من نوع الشّبكة العصبونيّة ذات الذّاكرة الطّويلة قصيرة المدى LSTM، وسيتمّ توضيح خطوات هذا التّطبيق في كلّ مرحلة مع الشّيفرات البرمجيّة والتّوابع الخاصّة بها [7]:
المرحلة الأولى : استدعاء المكتبات الأساسيّة:
حيث يتمّ استخدام مكتبات اس-كي للتّعلُّم Sklearn وتينسور فلو TensorFlow وكيراس Keras ومكتبة بايثون العدديَّة NumPy؛ لبناء النّموذج وإجراء المعالجة المسبقة للبيانات، لتحميل البيانات نستخدم مكتبة تحليل البيانات في بايثون (بانداس) Pandas ولرسم البيانات يتمّ استخدام مكتبة الرَّسم الرِّياضيّ في بايثون (ماتبلوت) Matplotlib، كما يتمّ استخدام مكتبة سيبورن Seaborn وهي مكتبة الرّسم الإحصائيّ في بايثون والتي تعتمد على مكتبة الرّسم الرّياضيّ (ماتبلوت) matplotlib، كما يتمّ استخدام مكتبة datetime والتي تقوم بالتّعامل مع التّواريخ والسّاعات.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from datetime import datetime
plt.style.use('fivethirtyeight')
import os
المرحلة الثّانية: هي مرحلة تحميل قاعدة البيانات:
أوّلًا: في حال استخدام منصّة جوجل كولاب Colab، سيتمّ الرّبط مع قرص جوجل google drive من أجل تحميل قاعدة البيانات التي سيتمّ دراستها، وذلك من خلال الشّيفرة البرمجيّة التّالية:
from google.colab import drive
drive.mount('/content/drive')
proj_path = '/content/drive/MyDrive/time/'
df=pd.read_csv(proj_path + "GOOGL.csv",parse_dates=["Date"],index_col=[0])
وقاعدة البيانات هي بيانات الأسهم الماليّة من جوجل Google Stock Data والتي تتضمّن معلومات عن البيانات اليوميّة للأسهم الماليّة لشركة غوغل وهي موجودة على الرّابط التّالي:
https://www.kaggle.com/datasets/varpit94/google-stock-data
ثمّ يتمّ استعراض الصّفوف الخمسة الأولى من قاعدة البيانات، حيث يُعبّر العمود الأوّل Date عن تاريخ اليوم، Open السّّعر ببداية اليوم المحدّد، Close السّعر بنهاية اليوم المحدّد، High أعلى سعر في اليوم المحدّد، Low أدنى سعر في اليوم المحدّد، Adj Close سعر الإغلاق المحدّد بعد أخذ بعض العوامل بعين الاعتبار، Volume حجم التّداول في اليوم المحدّد، وذلك من خلال الشّيفرة التّالية:
df.head()

ثمّ نقوم باستعراض معلومات إحصائيّة عن قاعدة البيانات المستخدمة مثل العدد الكلّيّ والمتوسّط والنّسب المئويّة وأصغر قيمة وأعلى قيمة لكلّ حقل من حقول قاعدة البيانات، وذلك من خلال الشّيفرة التّالية:
df.describe()

كما يتمّ استعراض الصّفوف الخمسة الأخيرة من قاعدة البيانات، وذلك من خلال التّعليمة التّالية:
df.tail()

ثمّ يتمّ حساب العلاقة بين كلّ عمود من أعمدة قاعدة البيانات، وذلك من خلال التّابع (Corr) ويحدّد مقدار التّرابط بينهم ويحدّد مقدار التّرابط بمجال بين 1 و -1؛ حيث كلّما كان النّاتج أقرب للواحد تكون العلاقة الطّردية بين المتغيّرين أكبر، أمّا في حال كانت القيمة أقرب لل -1 تكون العلاقة العكسيّة بين المتغيّرين أقوى، يتمّ عرض النّتائج في جدول:
corr = df.corr()
corr.style.background_gradient(cmap = 'coolwarm')

ثمّ يتمّ حساب مؤشّر القوّة النّسبيّة (RSI) Relative Strength Index، وهو مقياس يحدّد سرعة وتغيّر تحرّكات الأسعار، تكون قيمة مؤشّر القوّة النّسبية بين صفر و100، ويعبّر مؤشّر القوّة النّسبية عن ذروة الشّراء عندما تكون قيمته أكبر من 70 وذروة البيع عندما تكون قيمته أصغر من 30 وذلك بناء على معايير القوة الشّرائيّة المتّفق عليها عالميّا [8]، ثمّ يتمّ فصل القيم بناءً على قيم مؤشّر القوّة النّسبية كما يتمّ حساب المتوسّط المتحرّك Moving Average وهو أحد مؤشّرات التّحليل الماليّ وتتمثّل وظيفته الرّئيسيّة في تسوية الأسعار، وبالتّالي تقليل التّباينات المفاجئة للأسعار وإنشاء متوسّط سعر محدّث باستمرار [9]، ويمكن تحديد متوسّط الأسعار لفترات محدّدة. في هذا المقال قمنا بتحديد الفترة عند القيمتين 30 و100وذلك من خلال الشّيفرة البرمجيّة التّالية والتي تعبّر عن التّابع الرّياضيّ لمؤشّر القوّة النّسبيّة التي يتمّ حسابها بناء على قيمة مؤشّر الإغلاق كما يتمّ تحديد :
df['MA30'] = df['Adj Close'].rolling(window = 30).mean()
df['MA100'] = df['Adj Close'].rolling(window = 100).mean()
def get_RSI(df, column = 'Adj Close', time_window = 14):
# Return the RSI indicator for the specified time window
diff = df[column].diff(1)
# This preservers dimensions off diff values.
up_chg = 0 * diff
down_chg = 0 * diff
# Up change is equal to the positive difference, otherwise equal to zero
up_chg[diff >0] = diff[diff > 0]
# Down change is equal to negative difference, otherwise equal to zero
down_chg[diff < 0] = diff[diff <0]
# We set com = time_window-1 so we get decay alpha =1/time_window.
up_chg_avg = up_chg.ewm(com=time_window -1,min_periods = time_window).mean()
down_chg_avg = down_chg.ewm(com = time_window -1, min_periods = time_window).mean()
RS = abs(up_chg_avg/down_chg_avg)
df['RSI'] = 100 - 100 / (1 + RS)
return df
وباستعراض قاعدة البيانات بعد إضافة الحقول التي تعبّر عن الميزات المحسوبة؛ وهي مؤشر القوة النسبية RSI ومؤشر المتوسط المتحرك MA من أجل القيمتين 30 , 100 اي MA30 و MA100 نحصل على قاعدة المعلومات المحدثة التّالية:

ويتمّ رسم منحنٍ كما هو موضّح في الشّكل (4) يعبّر عن مؤشّر القوّة النّسبية (RSI) لقاعدة البيانات بشكل كلّيّ مع تحديد مستويين للفصل أعلى من 70 وأدنى من 30 وذلك بالنّسبة للزّمن وفق الشّيفرة التّالية:
plt.figure(figsize = (15,8))
plt.plot(df['RSI'])
plt.axhline(y = 70,color = 'red')
plt.axhline(y = 30,color = 'red')
plt.title('Relative Strength Index')

المرحلة الثّالثة: النّموذج المقترح:
نقوم باستخدام الشّيفرة البرمجيّة التّالية (كما هو موضّح في الشكل 5) لبناء النّموذج حيث يتمّ إضافة طبقة من الشّبكة العصبونيّة ذات الذّاكرة الطّويلة قصيرة المدى LSTM، ثمّ طبقتين من الشّبكات العصبونيّة الكثيفة DNN مع ضبط بارامتراتهم الأساسيّة، كما يتمّ تقسيم قاعدة البيانات إلى قسم تدريب وقسم اختبار ثمّ استعراض بارامترات النّموذج.
from tensorflow.keras.layers import LSTM
from tensorflow.keras.layers import Dense, Activation, Dropout, TimeDistributed
from tensorflow.keras.models import Sequential
X_train, y_train= np.array(X_train), np.array(y_train)
X_train = np.reshape(X_train, (X_train.shape[0], X_train.shape[1], 1))
model=Sequential()
model.add(LSTM(50,activation='relu', input_shape=(X_train.shape[1],1)))
model.add(Dense(25))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
model.summary()

يتمُّ تدريب النّموذج باستخدام بيانات التدريب من خلال الشّيفرة البرمجيّة التّالية:
model.fit(X_train, y_train, epochs=300, batch_size=100)

ثمّ يتمّ حساب نسبة الخطأ من أجل بيانات التّدريب والاختبار من خلال الشّيفرة التّالية:
test_data = train_df[train_len-2:]
X_val=[]
Y_val=[]
for i in range(2, len(test_data)):
X_val.append(test_data[i-2:i])
Y_val.append(test_data[i])
X_val, Y_val = np.array(X_val), np.array(Y_val)
X_val = np.reshape(X_val, (X_val.shape[0], X_val.shape[1],1))
prediction = model.predict(X_val)
from sklearn.metrics import mean_squared_error
# Know the model error accuracy | the model accuracy
lstm_train_pred = model.predict(X_train)
lstm_valid_pred = model.predict(X_val)
print('Train rmse:', np.sqrt(mean_squared_error(y_train, lstm_train_pred)))
print('Validation rmse:', np.sqrt(mean_squared_error(Y_val, lstm_valid_pred)))

وبرسم منحني توقّع النّموذج للبيانات مع منحني بيانات التّحقّق بالنّسبة للزّمن نحصل على الشّكل (6) حيث نلاحظ تقاربًا كبيرًا بين القيم التي تمّ التنبّؤ بها باستخدام النّموذج المدرّب وقيم التّحقّق المرجعيّة التي يتمّ المقارنة معها.
valid = pd.DataFrame(train_df[train_len:])
valid['Predictions']=lstm_valid_pred
plt.figure(figsize=(16,8))
plt.plot(valid[['High','Predictions']])
plt.legend(['Validation','Predictions'])
plt.show()

كذلك برسم منحني التوقّع للنّموذج المدرّب مع منحني التّدريب ومنحني التّحقّق، نلاحظ تقاربًا كبيرًا بين القيم التي تمّ التنبّؤ بها باستخدام النّموذج المدرّب وقيم التّحقّق المرجعيّة التي يتمّ المقارنة معها، وذلك موضّح بالشّكل (7):
train = train_df[:train_len]
valid = pd.DataFrame(train_df[train_len:])
valid['Predictions']=lstm_valid_pred
plt.figure(figsize=(16,8))
plt.title('Model LSTM')
plt.xlabel('Date')
plt.ylabel('Google Price USD')
plt.plot(train)
plt.plot(valid[['High','Predictions']])
plt.legend(['Train','Val','Predictions'])
plt.show()

الخاتمة:
هناك العديد من التّطبيقات اليوميّة المهمّة تعتمد بشكل أساسيّ على تقنيّة التّنبؤ بالسّلاسل الزّمنيّة، والتي تستخدم في التّطبيقات الاقتصاديّة والأرصاد الجوّيّة، وترتكز هذه التّقنيّة بشكل أساسيّ على خوارزميّات الذّكاء الاصطناعيّ التي حسّنت بشكل كبير من أداء هذه التّطبيقات؛ ولا سيّما النّموذج المذكور في هذه المقالة المعتمد على الشّبكات الإرجاعيّة، ويتمّ العمل على تطوير خوارزميّات أخرى تطوّر من أداء هذه التّطبيقات وتقييمها.
المراجع:
- unlocking-the-power-of-time-series-forecasting
- machine-learning-time-series-forecasting
- time-series-forecasting
- tutorial-time-series-forecasting
- https://aiinarabic.com/lstm/
- machine-learning-algorithms
- time-series-forecasting
- trading-investing/technical-analysis
- combining-relative-strength-index-with-moving-averages



تعليق واحد
جميل ، افادة رائعة بسيطة