تحسين المُعاملات في الشبكة العصبونيّة

المقدمة

نبدأ في تعلم الآلة بتحديد المهمة والنموذج الذي يتكون من البنية والمعاملات. ثم تأتي مرحلة تدريب النموذج والتي تعتبر بمثابة مسألة سد الفجوة بين ناتج تنبؤ النموذج وتصنيفات بيانات التدريب الحقيقية المتوقعة ويتم ذلك من خلال تحسين معاملات النموذج والذي لا يعتبر بالأمر السهل حيث تحدد قيمة المعاملات مدى دقة أداء النموذج للمهمة. لكن كيف يتم تحديد القيم الجيدة؟ الجواب ببساطة من خلال تحديد تابع الخسارة الذي يقيّم أداء النموذج والسعي لإنقاص قيمة الخسارة وبالتالي إيجاد قيم المعاملات التي تطابق التنبؤات مع الحقيقة. وهذا هو جوهر التدريب. وسنقوم في هذه المقالة بالشرح الموضح من خلال الرسوم البيانية التفاعلية لكيفية تطوير الحدس لضبط وحل مشكلة تحسين المعاملات.

1- تحديد مشكلة التحسين

يختلف تابع الخسارةمع اختلاف المهام واعتمادًا على الخرج المرغوب تكون قيمة هذا التابع صغيرة عند قيام النموذج بأداء المهمة بشكل جيد.  بالتالي سيؤثر أسلوب تحديده على تدريب وأداء النموذج. على فرض لدينا المثالين التاليين ونريد تحديد تابع الخسارة لكليهما.
المثال(1): التنبؤ بأسعار المنازل
المهمة هنا هي التنبؤ بأسعار المنازل  وذلك بناء على مساحة الطابق و عدد غرف النوم وارتفاع السقف. بالتالي يُعبَّر عن تابع الخسارة بالعبارة التالية:
“بإعطاء مجموعة مزايا المنازل. يجب أن يكون مربع الاختلاف بين قيمة التنبؤ والقيمة الحقيقية للسعر صغير قدر الإمكان”. 
 والعلاقة الرياضية تكون بالشكل: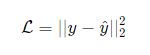حيث تمثل  السعر الحقيقي أو ما يسمى بالحقائق المرجعية ground truth وتمثل  القيمة المتنبأ بها. 

المثال (2):  تحديد مكان الأغراض Object localization
إن مهمة  تحديد مكان سيارة في مجموعة من الصور التي تحتوي على واحدة منها تُعتبر مهمة أكثر تعقيداً. يجب أن يمثل تابع الخسارة العبارة التالية بشكلها الرياضي:
“بإعطاء صورة تحوي سيارة وحيدة. يجب التنبؤ بمربع الإحاطة bbox للعربة. المربع المتنبّأ به يجب أن يطابق حجم وموقع السيارة الفعلية قدر الإمكان”. 
و بالشكل الرياضي يكون تابع الخسارة المحتمل هو:يعتمد تابع الخسارة السابق على:
1- تنبؤ النموذج الذي يعتمد بدوره على قيم المعاملات (الأوزان) بالإضافة إلى الدخل (في هذه الحالة الصور).
2- الحقائق المرجعية المطابقة للدخل (مربعات الإحاطة).

 

تابع الكلفة

يكون دخل تابع الخسارة مثال وحيد بالتالي القيام بإنقاص قيمته لا يضمن إيجاد معاملات نموذج أفضل من أجل أمثلة أخرى. ومن المعروف أنه يجب إنقاص معدل الخسارة المحسوبة على كامل مجموعة بيانات التدريب عندها يدعى التابع بتابع الكلفة.

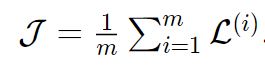
 حيث تمثل  m حجم بيانات التدريب و هي خسارة مثال تدريب وحيد ذو تصنيف.
يساعد هذا التابع الشبكة على تصحيح أو تغيير المعاملات لتقليل الأخطاء. ويمثل المسافة أو الاختلاف بين القيمة المتوقعة والقيمة الحقيقة. ويتم تخمينه من خلال تكرار تشغيل النموذج لمقارنة القيمة المتنبأ بها مع قيمة الحقائق المرجعية المعروفة.
بالتالي الهدف من نموذج تعلّم الآلة هو إيجاد المعاملات والأوزان أو البنية التي تعمل على إنقاص قيمة تابع الكلفة.

التمثيل البياني لتابع الكلفة

من أجل مجموعة من الأمثلة مع الحقائق المرجعية للتصنيفات، يختلف شكل تابع الكلفة باختلاف معاملات الشبكة. على الرغم من أنه من الصعب رسم التمثيل البياني لتابع الكلفة في حال كان هناك أكثر من معاملين للشبكة إلا أنّ الرسم البياني موجود والهدف منه هو إيجاد نقطة يكون فيها تابع الكلفة أصغر ما يمكن وتعديل قيم المعاملات سيحرك القيمة إمّا أقرب أو أبعد من النقطة الصغرى الهدف.

الفرق بين تابع الكلفة و النموذج

من المهم التمييز بين التابع الذي يمثل النموذج والذي يقوم بالمهمة والتابع  الذي يمثل تابع الكلفة والذي يجب القيام بتحسينه.

•  يأخذ النموذج مثال غير مصنف كدخل على سبيل المثال صورة ويعطي التصنيف (مثل مربع الإحاطة للسيارة) كخرج. قيم المعاملات المحسّنة ستمكن النموذج من أداء المهمة بدقة نسبية.
• أمّا تابع الكلفة يأخذ مجموعة من المعاملات كدخل ويعطي الكلفة كخرج. ويقوم بقياس مدى جودة أداء هذه المعاملات للمهمة(في مجموعة التدريب).

تحسين تابع الكلفة

في البداية تكون القيم الجيدة للمعاملات غير معروفة. لكن لدينا صيغة دالة الكلفة ومن خلال إنقاص قيمتها سنجد القيمة الجيدة لهذه المعاملات. ويتم إنقاص القيمة من خلال تغذية بيانات التدريب إلى النموذج وضبط المعاملات بشكل متكرر لجعل الكلفة صغيرة قدر الإمكان.
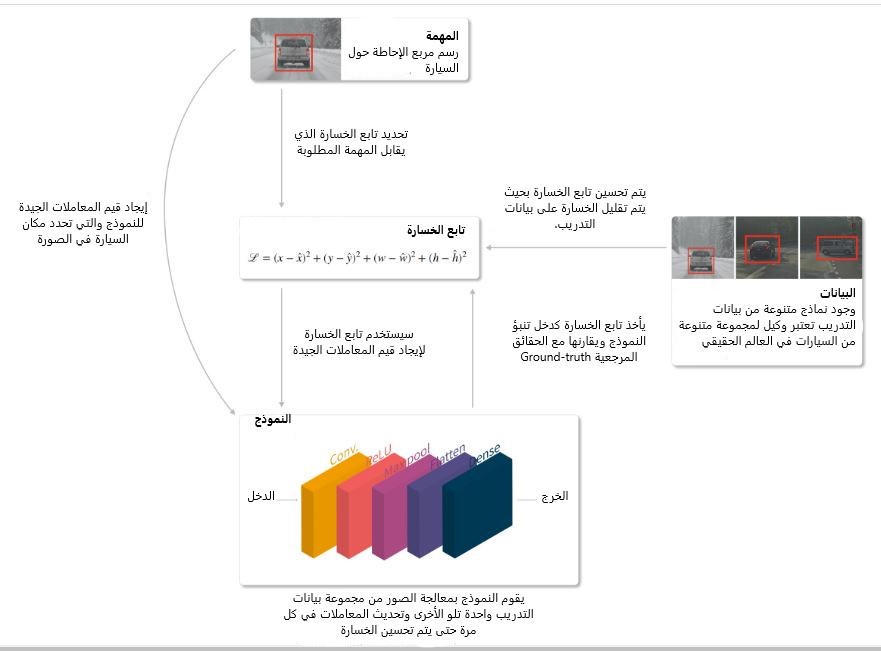
وباختصار، سيكون للطريقة التي تُحدّد بها دالة الكلفة الدور في تحديد أداء النموذج في المهمة قيد التنفيذ. يوضح الرسم البياني أدناه آلية العثورعلى نموذج يعمل بشكل جيد.

2- تشغيل عملية التحسين

سنفترض في هذا القسم أنه تم اختيار مهمة ومجموعة بيانات وتابع كلفة. وسنحاول تقليل الكلفة لإيجاد أفضل قيم للمعاملات.

استخدام انحدار المشتق

لإيجاد قيم المعاملات التي تحقق أقل قيمة لتابع الكلفة يمكن محاولة استنتاج شكل مغلق close form ( أسلوب لحل مشكلة في سلسلة منتهية من العمليات الجبرية على سبيل المثال إيجاد نقطة تحقق أقل قيمة للتابع من خلال حل المعادلة والتي تؤدي إلى جعل ) إمّا جبريًا أو تقريبيًأ باستخدام طريقة تكرارية. وفي تعلّم الآلة الطرق التكرارية مثل انحدار المشتق تعتبر غالبًا الخيار الوحيد على اعتبار أن تابع الكلفة يعتمد على عدد  كبير من المتحولات بالتالي عدم وجود طريقة عملية لإيجاد الحل.
في انحدار المشتق يجب أولًا تهيئة قيم المعاملات أي تحديد نقطة بداية للتحسين ومن ثم ضبط هذه القيم بشكل تكراري لتقليل قيمة تابع الكلفة. في كل تكرار يتم ضبط المعاملات بشكل معاكس لمشتق الكلفة أي في الاتجاه الذي يقلل من الكلفة.
أو من أجل x ضمن مجموعة بيانات التدريب صيغة انحدار المشتق تعطى بالشكل: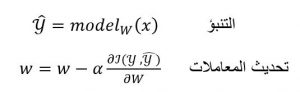


حيث تمثل تنبؤ النموذج لدخل معطى .
تمثل المعاملات.
يمثلالمشتق ويشير إلى الجهة التي يجب دفع المعاملات بها  لانقاص قيمة تابع الخسارة.
يمثلمعدل التعلم والذي من الممكن ضبطه لتحديد مقدار ضبط قيمة المعاملات في التكرار الواحد.
رأينا أنه لحساب تابع الكلفة يجب المرور على كامل مجموعة بيانات التدريب بالتالي حساب هذا التابع عند كل تكرار قد يكون بطيء. يمكن عوضًا عن ذلك حساب معدل الخسارة لدفعة مصغّرة من البيانات بالعلاقة: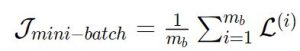 
حيث أن  تمثل حجم الدفعة batch size وتعتبر المفتاح الأساسي في ضبط المعاملات الأساسية بالتالي القيام بإنقاص قيمة هذا التابع يؤدي إلى تسريع تحديث المعاملات بالشكل الذي يقلل من خطأ التدريب.

 

ضبط المعاملات الأساسية لانحدار المشتق

من أجل استخدام انحدار المشتق يجب ضبط قيم المعاملات الأساسية مثل معدّل التعلّم وحجم الدفعة بشكل مناسب لأنها ستؤثر على عملية التحسين. في الشكل أدناه يمكن اكتشاف المعاملات المستخدمة في إنشاء مجموعة التدريب. حيث تُعطى قيم الحقائق المرجعية والتي تم من خلالها إنشاء البيانات(الخط الأزرق) لنتمكن من مقارنتها مع النموذج المدرب(الخط الأحمر). ومع تغيير نقطة التهيئة ومعدّل التعلّم وحجم الدفعة يمكن الحصول على الإجابة لبعض التساؤلات مثل: لماذا تتقارب معاملات النموذج لقيم تختلف عن الحقائق المرجعية؟ وما تأثير حجم مجموعة بيانات التدريب؟ ما تأثير معدّل التعلّم على التحسين؟ ولماذا يبدو منحنى الكلفة بهذا الشكل؟

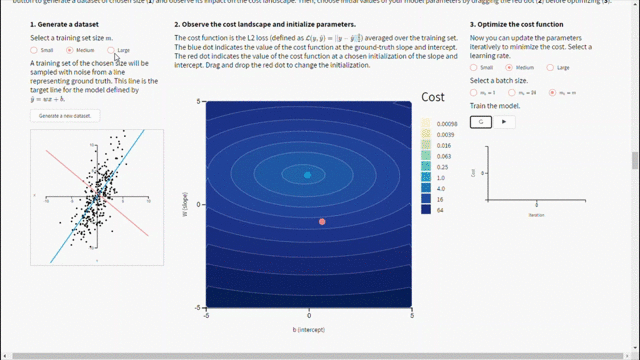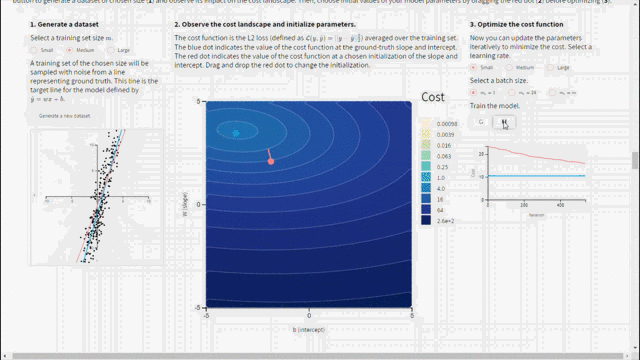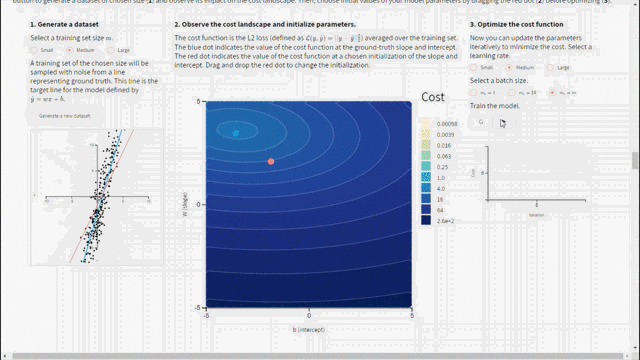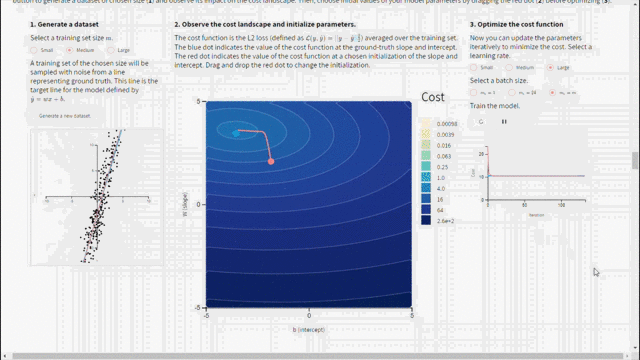
نستنتج من الشكل السابق مايلي:
– رغم  اختيار أفضل المعاملات الأساسية الممكنة لن يتطابق النموذج المدرب مع الحقائق المرجعية المعطاة (الخط الأزرق) لأن مجموعة بيانات التدريب تعتبر بمثابة وكيل لتوزع الحقائق المرجعية.
– كل ما كان حجم مجموعة بيانات التدريب أكبر كل ما كانت معاملات النموذج المدرّب أقرب إلى المعاملات المستخدمة في إنشاء البيانات.
– في حال كان معدّل التعلّم كبير جدًا  لن تتقارب الخوارزمية أّما في حال كان صغير جدًا ستتقارب لكن ببطء.
– في حال كانت نقطة التهيئة الأولية (النقطة الحمراء) قريبة من الحقيقة المرجعية وتم ضبط المعاملات الأساسية (معدّل التعلّم وحجم الدفعة) بشكل صحيح عندها ستتقارب الخوارزمية بسرعة.
مما سبق نرى أن كل معامل أساسي له تأثير مختلف على تقارب الخوارزمية. لنلقي نظرة أعمق على المعاملات الأساسية.

التهيئة Initialization

تسرع التهيئة الجيدة من عملية التحسين و التقارب من الحد الأدنى أو في حال كان هناك العديد من الحدود الدنيا من أفضلها. لمعرفة المزيد عن التهيئة يمكن قراءة مقالتنا تهيئة الشبكات العصبونية.

معدّل التعلّم Learning rate

يؤثر معدّل التعلّم على تقارب عملية التحسين كما أنه يوازن تأثير انحناء تابع الكلفة. وفقًا لصيغة انحدار المشتق أعلاه يُعطى اتجاه وحجم تحديث المعاملات من خلال معدّل التعلّم مضروبًأ بمنحدر تابع الكلفة slope عند نقطة معينة  .
عندما يكون معدّل التعلّم صغير جدًأ عندها التحديث سيكون صغير والتحسين يتم ببطء وخاصة عندما يكون منحنى الكلفة منخفض ومن المرجح أن يستقر التحديث في النهاية المحلية  local minimum (حيث قيمة التابع في هذه النقطة تكون أصغر من النقاط القريبة لكن من المحتمل أن تكون أكبر من نقطة بعيدة) أو الهضبة المحلية local plateau (مذكورة لاحقًا).
وعندما يكون معدّل التعلّم كبير جدًأ عندها التحديث سيكون كبير ويختلف التحسين خاصة عندما يكون انحناء تابع الكلفة مرتفع.
في حال تم اختيار معدّل التعلّم بشكل جيد ستكون التحديثات مناسبة و يتقارب التحسين إلى مجموعة معاملات جيدة.
الشكل التالي يساعد على فهم تأثير معدّل التعلّم وانحناء تابع الكلفة على تقارب الخوارزمية.

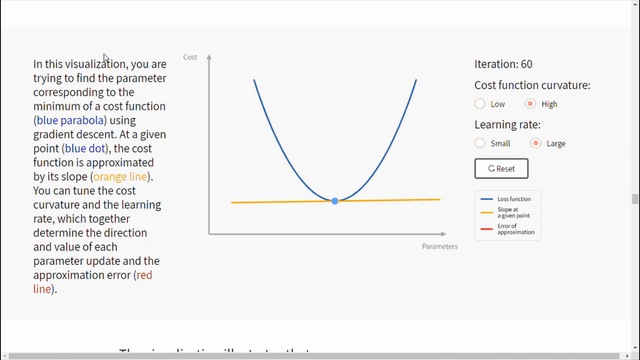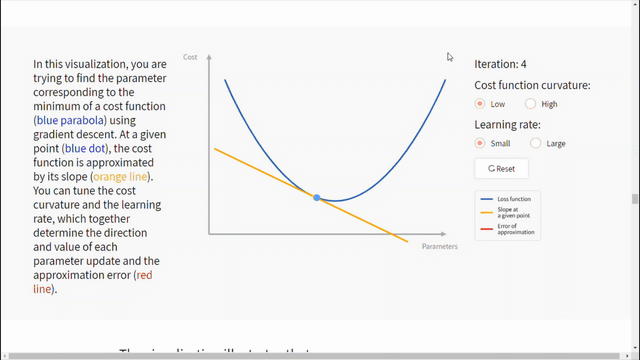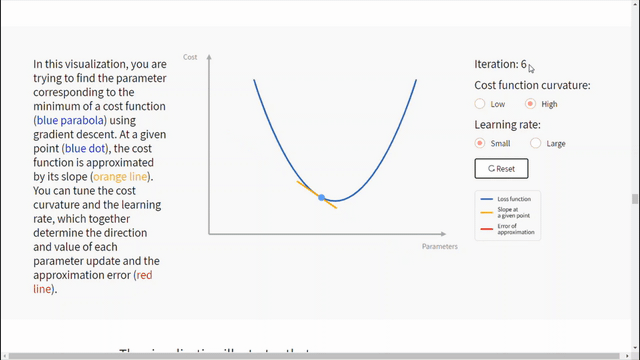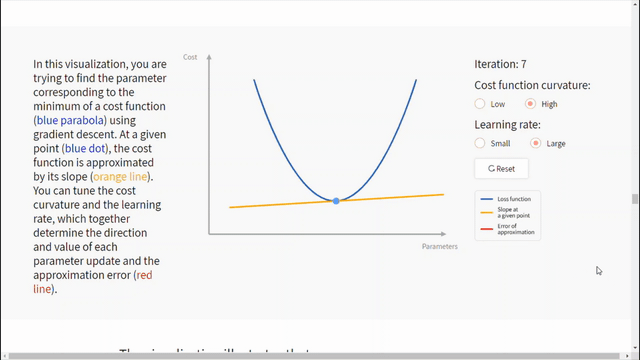
نستنتج من الشكل السابق مايلي:

•  يعتمد معدّل التعلّم الجيد  على منحنى تابع الكلفة.
• انحدار المشتق يعمل على التقارب الخطي لتابع الكلفة في نقطة معطاة. ثم يتحرك للأسفل على طول القيمة التقريبية لهذا التابع.
• في حال كان منحنى تابع الكلفة شديد الانحناء عندها معدّل التعلّم الأكبر (حجم الخطوة) سيزيد من احتمال تجاوز الخوارزمية للحد. أما في حال أخذ خطوة أقل أي معدّل تعلّم أصغر سيقلل من مشكلة تجاوز الحد لكن سيكون التعلّم أبطأ.

من الشائع البدء بمعدّل تعلّم كبير مثلًا بين 0.1 و 1 و من ثم تصغير هذه القيمة خلال التدريب. اختيار مقدار تضاؤل decay صحيح (مقداره وعدد المرات) أمر مهم. حيث يبطّئ مجدّول التضاؤل decay schedule السريع التقدم نحو الحل الأمثل . بينما يؤدي مجدّول التضاؤل البطيء إلى تحديثات فوضوية مع تحسينات صغيرة. لذلك يعتبر إيجاد أفضل مجدّول تضاؤل best decay schedule  ليس بالأمر السهل. ومع ذلك تساعد خوارزميات ملاءمة معدّل التعلّم مثل زخم الحركة Momentum و جذر متوسط مربع الانتشار(آر إم إس بروب)  RMSprop في تعديل معدّل التعلّم خلال عملية التحسين و سنشرح هذه الخوارزمية لاحقًأ.

حجم الدفعة Batch size

يمثل حجم الدفعة عدد ن أمثلة البيانات المستخدمة لتدريب النموذج في كل تكرار. الدفعات الصغيرة المثالية هي 32, 64, 128, 256, 512 بينما الدفعات الكبيرة قد تكون ألاف الأمثلة.
من المهم اختيار حجم دفعة صحيح لضمان التقارب بين تابع الكلفة وقيم المعاملات و ليصبح النموذج قادر على التعميم. وقد قام بعض الباحثون بدراسة كيفية الاختيار الصحيح وأعطت الأبحاث في حجم الدفعة المبادئ التالية:

1. يحدد حجم الدفعة عدد مرات التحديث. فكلما  كان حجم الدفعة أقل كلما زادت سرعة التحديثات. 
2. كلما كان حجم الدفعة أكبر كلما كان مشتق الكلفة أكثر دقة بالنسبة للمعاملات.أي أن التحديث يتجه نحو الانحدار المحلي local slope لتابع الكلفة.
3. إن اختيار حجم دفعة كبير دون أن يكون كبير جدًأ و بحيث يتناسب مع ذاكرة معالج الواجهات الرسومية GPU يساعد على تحسين فعالية التفرعية و تسريع التدريب. 
4. اقترح بعض الباحثين (Keskar et al., 2016) [2]أيضًا أن أحجام الدفعة الكبيرة من الممكن أن تجعل النموذج غير قادر على التعميم ربما بسبب جعل الخوارزمية تقع في مشكلة الحل الأمثل المحلي   local optima أو هضبة محلية  أكثر سوءًأ.

مشكلتي الحل الأمثل المحلي local optima و الهضبة المحليّة local plateau:
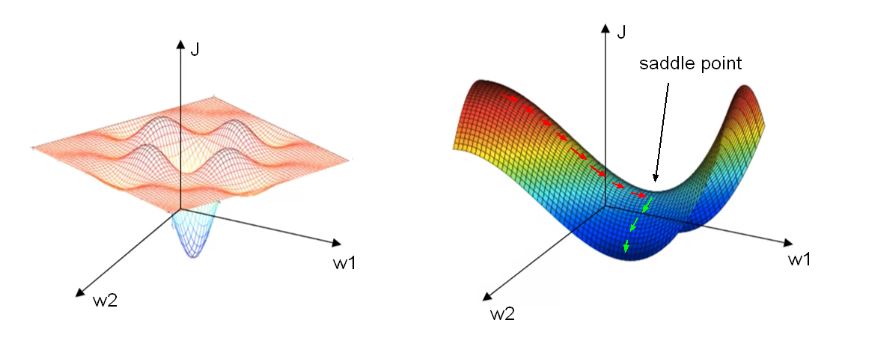
بالنظر إلى الجانب الأيسر من الشكل(4) سنرى أنه من الشائع البقاء عالقين في النهاية المحلية  بدلًأ من إيجاد الطريق إلى الحل الأمثل العام (global optima:حيث قيمة التابع في هذه النقطة أكبر من أي نقطة أخرى). 
في الواقع معظم النقاط ذات المشتق الصفري لا تشكل الحل الأمثل المحلي لكن عوضًأ عن ذلك تشكل ما يدعى نقطة السرج saddle (الجانب الأيمن من الشكل (4)) والتي تتسبب في مشكلة الهضاب وهي منطقة يكون فيها المشتق قريب من الصفر لفترة طويلة. تبطئ هذه المشكلة من عملية التدريب. (السهم الأحمر في الشكل يمثل مشكلة الهضبة) في الواقع تأخذ العملية وقت طويل قبل أن تتبع المسار الأخضر للوصول إلى النهاية المحلية.

عند اختيار حجم الدفعة هناك توازن يجب تحقيقه اعتمادًا على الأجهزة الحاسوبية المتاحة والمهمة التي يجب تحقيقها.

التحديث التكراري Iterative update

بعد تحديد نقطة البداية ومعدّل التعلّم وحجم الدفعة حان الآن دور تحديث المعاملات بشكل تكراري لتوجيه تابع الكلفة إلى النهاية المحلية. وكذلك تحديد خوارزمية التحسين و التي تعتبر خيارًا أساسيًا. يساعد الشكل التالي على فهم إيجابيات وسلبيات كل خوارزمية على حدا وهو يهدف إلى تغيير المعاملات الأساسية لإيجاد قيم المعاملات التي تقلل من قيمة تابع الكلفة وذلك من خلال اختيار تابع الكلفة ونقطة بداية التحسين. وعلى الرغم من عدم وجود نموذج واضح يمكن أن نفترض بأن إيجاد النهاية المحلية  لتابع الكلفة مكافئ لإيجاد أفضل نموذج للمهمة و من أجل التبسيط، فإن النموذج لديه معاملين فقط وحجم دفعة مساوي للـ1 بشكل دائم.

اختيار المحسن Choice of optimizer

يؤثر اختيار المُحسّن على كل من سرعة التقارب وما إذا كان يحدث بالفعل. وقد تم تطوير العديد من البدائل لخوارزميات تدرج المشتق الاعتيادية gradient descent algorithms في السنوات القليلة الماضية وهي مدرجة أدناه. مع ملاحظة أن .

1- انحدار المشتق العشوائي (Stochastic Gradient Descent):
– يمكن أن يستخدم انحدار المشتق التفرعية بشكل فعّال لكن سيكون بطيء جدًا عندما تكون مجموعة التدريب أكبر من ذاكرة معالج الواجهات الرسومية GPU عندها لن تكون التفرعية بشكلها الأمثل.
– عادة يتقارب انحدار المشتق العشوائي بشكل أسرع من انحدار المشتق الاعتيادي على مجموعة بيانات كبيرة باعتبار التحديثات أكثر تكرارًا بالإضافة إلى ذلك عادة ما يكون التقريب العشوائي للانحدار دقيقًا دون استخدام مجموعة البيانات بأكملها لأن البيانات غالبًا ما تكون زائدة عن الحاجة.
– من بين جميع المحسنات التي ستذكر في هذا الجدول يستخدم انحدار المشتق العشوائي ذاكرة أقل عند حجم دفعة معين.
علاقة التحديث تعطى بالعلاقة:

2- زخم الحركة Momentum: 
 عادة ما يسرّع هذا المحسّن عملية التعلّم بتغيير طفيف في التنفيذ ويستخدم ذاكرة أكبر لحجم دفعة معينة من محسنّ انحدار المشتق العشوائي ولكن أقل من المحسّنين آر إم إس بروب و آدم.
علاقة التحديث تعطى بالعلاقة: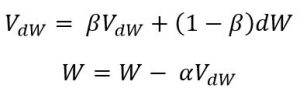

3- آر إم إس بروب (RMSprop):
 يمنع عادة ملائم معّدل التعلّم آر إم إس بروب  من تضاؤل معدّل التعلّم بشكل سريع أو بطيء جدًأ. وهو يحافظ على معدلات التعلّم لكل معامل ويستخدم ذاكرة لحجم دفعة معينة أكبر من انحدار المشتق العشوائي و زخم الحركة ولكن أقل من محسنّ آدم.
علاقة التحديث تعطى بالعلاقة: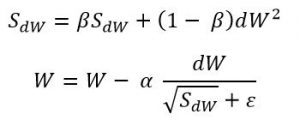
4- أدم Adam: 
– المعاملات الأساسية لآدم (معدّل التعلّم، معدلات التضاؤل الأسّيّة للتقديرات اللحظية…) عادة يتم تعيينها بقيم محددة مسبقًأ (موجودة في رابط المحسنّ) وليس من الضروري ضبطها. ينفذ آدم شكلًا من أشكال تلدين معدّل التعلّم learning rate annealing بأحجام خطوات تكيّفيّة  [5]
– من بين جميع المحسنات التي ذكرت في الجدول يستخدم آدم أكبر قدر من الذاكرة لحجم دفعة معينة. غالبًأ ما يكون آدم هو المحسّن الافتراضي في تعلم الآلة.
علاقة التحديث تعطى بالعلاقة: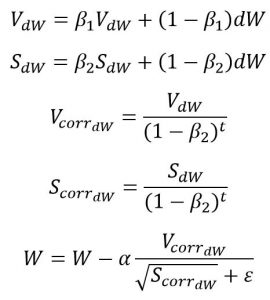

تؤدي خوارزميات تحسين الملاءمة مثل آدم أو أر إم إس بروب أداءً جيدًا في الجزء الأول من التدريب ولكن تبين تم ايجادأنها ذات قدرة  ضعيفة على التعميم في المراحل اللاحقة مقارنة مع انحدار المشتق العشوائي.

الخاتمة

يمكن أن يساعد استكشاف خوارزميات التحسين وقيم المعاملات الأساسية في بناء حدس لتحسين الشبكات لتقوم بمهام مختلفة. وأثناء البحث عن المعاملات الأساسية من المهم فهم حساسية التحسين لمعدّل التعلّم وحجم الدفعة والمحسّن وما إلى ذلك. حيث يساعد ذلك جنبًا إلى جنب مع اختيار الطريقة الصحيحة (البحث العشوائي أو التحسين البايزي (الإحصائي) Bayesian optimization) في العثور على النموذج الصحيح.

المراجع

[1]-Parameter optimization in neural networks
[2]-Learning Rate Decay and Local Optima
[3]-Improving Deep Neural Networks, Week 2
[4]-Local vs. Global Optima
[5]-Setting the learning rate of your neural network.