التدّقيق العلمي: د. م. حسن قزّاز، م. محمّد سرميني
التدّقيق اللّغوي: هبة الله فلّاحة

المقدّمة:

سبق وتطرّقنا في مقالٍ سابقٍ إلى الإلمام بالجوانب العامّة الأساسيّة للتّعلّم المعزّز (Reinforcement Learning) بسردٍ لأهمّ العناصر المكوّنة له والّتي تعتبر بمثابة حجر الأساس، وذلك بغية فهم آليّة التّفاعل المتكاملة والمتوازنة والمتناغمة فيما بينها، مع الإشارة إلى أنّ جذور هذا النّوع من التّعلّم مكتسبةٌ ومستمدّةٌ من خلال محاكاة طريقة سلوكنا وتصرّفنا (Action) نحن البشر (Agent) وتفاعلنا مع البيئة (Environment) المحيطة بنا بغضّ النّظر عن طبيعتها وذلك تحت مسمّى “فضول الاكتشاف ” للتّعلّم عن طريق التّجربة والخطأ.

إذًا، يمكنك عزيزي القارئ إمّا الاطّلاع على مقالتنا السّابقة حول أساسيّات التّعلّم المعزّز لتكوين المظهر النّهائيّ له من خلال فهم المناهج والخوارزميّات المتّبعة ضمنه في مقالتنا اليوم، أو يمكنك استرجاع أهمّ النّقاط الواردة فيه بشكلٍ سريعٍ لتجنّب ضياع وتشتّت الأفكار وذلك من خلال الرّابط هنا.

التّعلّم المعزّز:

كما تمّ ذكره سابقًا فإنّ التّعلّم المعزّز (Reinforcement Learning) من إحدى تقنيّات تعلّم الآلة (Machine Learning) القائمة على التّغذية الرّاجعة (feedback)، حيث يتعلّم فيها الوكيل التّصرّف في البيئة من خلال تنفيذ الإجراءات ورؤية النّتائج المتعلّقة بها، فهنا الهدف الأوّل والأخير للوكيل (agent) تعظيم المكافأة (reward) الّتي يحصل عليها؛ وليس العثور على أنماطٍ (patterns) مخفيّةٍ كما هو متعارفٌ عليه في التّعلّم غير الخاضع لإشرافٍ (Unsupervised Learning) [1].

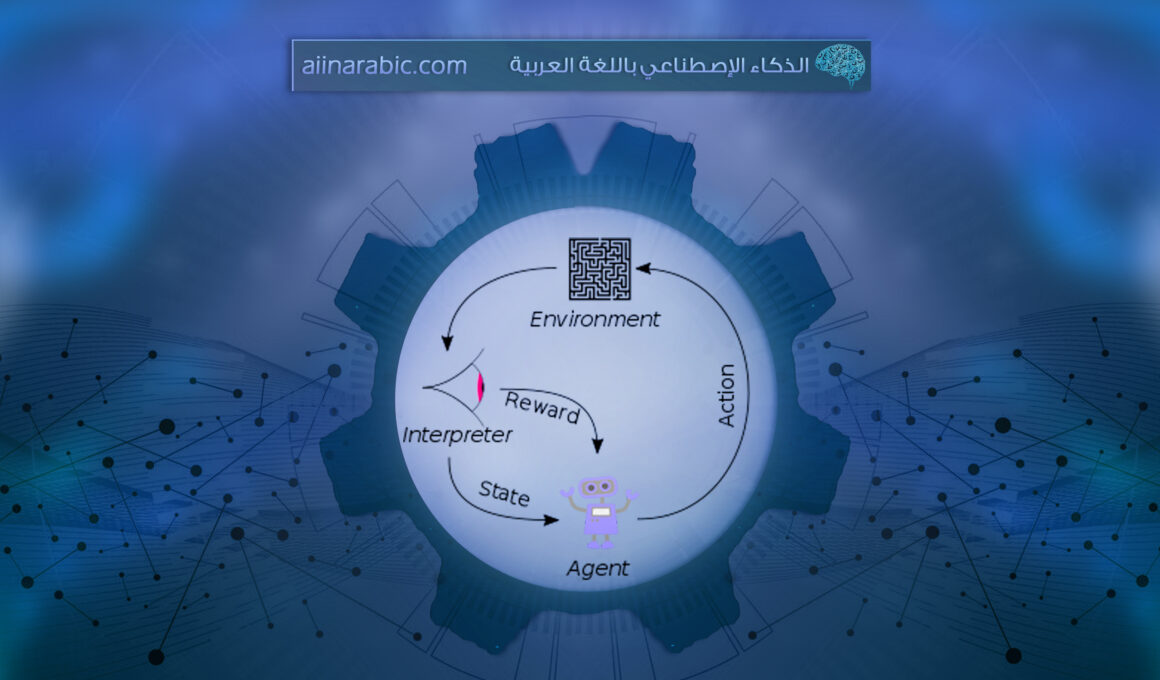
ولكن قبل المضيّ في الحديث عن أبرز الخوارزميّات الّتي احتلّت أهميّةً كبيرةً في هذا المجال، لابدّ لنا من التّذكير بشكلٍ مقتضبٍ بعناصر الارتكاز الأساسيّة للتّعلّم المعزّز والمتمثّلة بالشّكل (1) التّالي [2]:

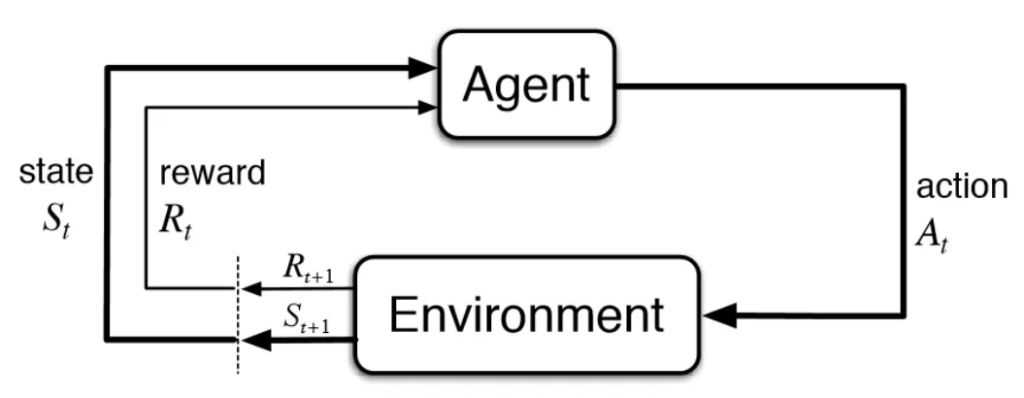
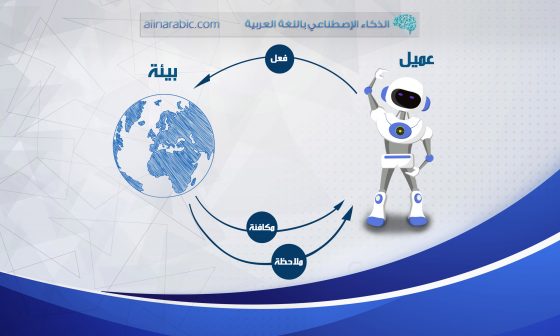
• البيئة (Environment): هي الوضع المحاط به الوكيل، وفي التّعلّم المعزّز نفترض أنّ البيئة عشوائيّةٌ في طبيعتها.
• الوكيل (Agent): هو كيانٌ يمكنه إدراك وفهم واستكشاف البيئة والتّصرّف وفقًا لها.
• الإجراء (Action): وهو يمثّل جميع الحركات الممكنة والمتاحة للوكيل من أجل اتّخاذها.
• الحالة (State): وهي الوضع المعاد من قبل البيئة بعد اتّخاذ الوكيل لكلّ إجراءٍ من فضاء الإجراءات المتاحة.
• المكافأة (Reward): وهي العائد المباشر الّذي يتمّ إرساله من قبل البيئة للوكيل بغية تقييم الإجراء الأخير المتّبع من قبله.

1-2- السّمات الأساسيّة للتّعلّم المعزّز:

• عدم اطّلاع ومعرفة الوكيل في التّعلّم المعزّز بهيكليّة البيئة الّتي يتفاعل معها، والإجراءات المثلى الواجب اتّخاذها عند حالةٍ معيّنةٍ.
• اعتماد التّعلّم المعزّز في آليّة عمله على الاكتشاف والتّجربة.
• اتّخاذ الوكيل للإجراء التّالي وتغييره لحالة البيئة اعتمادًا على ملاحظات ونتائج (feedback)الإجراء السّابق.
• حصول الوكيل في بعض الأحيان على مكافأةٍ متأخّرةٍ.
• عشوائيّة البيئة الخاصّة بهذا التّعلّم والّتي تخلق الحاجة لدى الوكيل لاستكشافها، من أجل الحصول على أقصى قدرٍ ممكنٍ من المكافآت الإيجابيّة [2].

2-2- تطبيقات التّعلّم المعزّز:

• علم الرّوبوتات: يتمّ استخدام التّعلّم المعزّز في الملاحة، وكرة القدم الآليّة، والمشي وما إلى ذلك.
• معالجة اللّغات الطّبيعيّة: يتمّ استخدام التّعلّم المعزّز في إجراء العديد من مهام مُعالجة اللّغات الطبيعيّة (NLP) مثل الإجابة على الأسئلة (Question Answering)، التّلخيص (Summarization) وبناء روبوتات الدّردشة (ChatBot) وكلّ هذا بواسطة وكيل التّعلّم المعزّز.
• التّحكّم: يتمّ استخدام التّعلّم المعزّز في التّحكّم الكيفيّ مثل التّحكّم بعمليّات المصنع، والتّحكّم في الدّخول في الاتّصالات وأيضًا التّحكّم  بطيّار الهيليكوبتر.
• الزّراعة: يتمّ استخدام التّعلّم المعزّز في الزّراعة لفوائده الجمّة في إطار القرارات الواجب اتّخاذها أثناء زراعة المحصول، مثل تحديد كمّية السّماد والرّيّ الواجب استخدامها وتوقيت كلّ واحدةٍ منهما.
• المشاركة في مباريات الألعاب:  يمكن استخدام التّعلّم المعزّز في لعبة الشّطرنج (chess) ولعبة (X_O) أي (tic-tac-toe) ولعبة ماريو (Mario) وغيرها.
• علم الكيمياء: يمكن استخدام التّعلّم المعزّز في تحسين التّفاعلات الكيميائيّة.
• العمل: يتمّ الآن إدخال التّعلّم المعزّز في العمل، من أجل تخطيط استراتيجيّة العمل.
• التّصنيع: يتمّ استخدام التّعلّم المعزّز العميق (Deep Reinforcement Learning) ضمن الرّوبوتات في العديد من شركات تصنيع السّيّارات، من أجل التقاط البضائع الجيّدة ووضعها في بعض الحاويات.
• قطاع الموارد الماليّة: يتمّ استخدام التّعلّم المعزّز حاليًا في القطاع الماليّ، من أجل تقييم استراتيجيّات التّجارة [2] [4].

خوارزميّات وأطر العمل الرّياضيّة في التّعلّم المعزّز:

لو تناولنا كمثالٍ لعبة الأتاري (Atari Game) سنلاحظ بإسقاطٍ بسيطٍ أنّ البيئة (environment) هي اللّعبة بحدّ ذاتها أمّا الوكيل فيمثّل خوارزميّة التّعلّم المعزّز (RL Algorithm)، حيث تبدأ البيئة بإرسال حالةٍ إلى الوكيل واعتمادًا على معرفة الأخير (Knowledge) يتمّ اتّخاذ إجراءٍ (action) استجابة للحالة المتواجد فيها، وبعد ذلك تقوم البيئة بإرسال زوجٍ مكوّنٍ من الحالة التّالية والمكافأة المعادة إلى الوكيل (next state, reward)، وهكذا سيقوم الوكيل في النّهاية بتحديث معرفته بالمكافأة المرسلة له من قبل البيئة من أجل تقييم الإجراء الأخير الّذي قام باتّخاذه، تستمرّ هذه الحلقة إلى أن ترسل البيئة حالة نهائيّة (terminal state) والّتي من شأنها إنهاء الحلقة (episode).

طبعًا إنّ غالبيّة خوارزميّات التّعلّم المعزّز تتبع هذا النّمط من العمل، وستلاحظ ذلك بمفردك عزيزي القارئ بقليلٍ من التّركيز المنصبّ في كلّ واحدةٍ على حدة [3].

ولكن قبل الاستفاضة في شرحها يجب علينا التّفريق بين نوعي السّياسة التّاليين:

(on-policy) في هذه السّياسة يتعلّم الوكيل القيمة (value) اعتمادًا على الإجراء الحاليّ المشتقّ من السّياسة الحاليّة، أي أنّ هذه الطّرق تحاول تقييم وتحسين السّياسة ذاتها المستخدمة لاتّخاذ القرارات، فهنا لدينا السّياسة السّلوكيّة تساوي السّياسة الهدف (Target policy=Behavior policy) كأمثلةٍ عنها لدينا  خوارزميّة تكرار القيمة (Value Iteration) وتكرار السّياسة (Policy Iteration).

بينما يتمّ تعلّم السّياسة (off-policy) اعتمادًا على الإجراء a* (الإجراء الأمثل الّذي يتمّ اختياره بطريقةٍ جشعةٍ Greedy من بين مجموعةٍ من الإجراءات المتاحة للوكيل من أجل تعظيم قيمة الحالة) الّذي تمّ الحصول عليه واكتسابه  من سياسةٍ أخرى، أي أنّ هذه الطّرق تقيّم وتحسّن سياسة مختلفة عن السّياسة المستخدمة في اتّخاذ القرارات (Target policy!=Behavior policy)، حيث أنّ السّياسة الأولى السّلوكية (Behavior policy) يستخدمها الوكيل من أجل اكتشاف البيئة أي اختيار الإجراءات ليتفاعل معها، في حين أنّ السّياسة الثّانية الهدف (Target policy) يستخدمها الوكيل للتّعلّم من المكافأة المعادة إليه من قبل البيئة نتيجة تطبيقه لفعلٍ معيّنٍ، بحيث يتمّ الاستفادة منها في تعديل قيم أزواج (حالة_إجراء) فمثلًا في خوارزميّة (Q-learning) ستكون السّياسة المطبّقة هي السّياسة الجشعة (Greedy policy) وهذا ما سنتكلّم عنه في مقالٍ لاحقٍ [3].

1-3- عمليّة ماركوف لاتّخاذ القرار (Markov Decision Process=MDP) :

هي خوارزميّة تعلّمٍ معزّزٍ تمنحنا الطّريقة لتشكيل ودعم عمليّة اتّخاذ قرارٍ متسلسلٍ، وتتضمّن هذه الخوازرميّة صانع القرار (decision maker) والّذي يدعى بالوكيل (agent) المسؤول عن إحداث التّفاعلات مع البيئة الموضوع فيها، حيث تحدث هذه التّفاعلات بشكلٍ متعاقبٍ، أي باختصارٍ هي عبارةٌ عن إطار عملٍ يمكن استخدامه لتوليد سياساتٍ من أجل التّحكّم مثلًا بحركة الرّوبوت.

في كلّ خطوةٍ زمنيّةٍ معيّنةٍ سيحصل الوكيل على بعض التّمثيل الخاصّ بحالة البيئة المرتبط بها حاليًّا، وكما أسلفنا سابقًا في لعبة (Atari) سيختار الوكيل إجراءً من بين مجموعةٍ من الخيارات المتاحة ليتمّ بعدها نقل البيئة لحالةٍ جديدةٍ ومنح الوكيل مكافأة بفضل إجرائه السّابق.

تكرار هذه العمليّة من شأنه أن يخلق شيئًا يدعى بالمسار (trajectory) الّذي يظهر تسلسلًا من الحالات (states)، والإجراءات (actions) والمكافآت (rewards).

إنّ الهدف الأساسيّ من خوارزميّة (MDP) يقبع بين يديّ الوكيل سعيًا منه لتعظيم العائد الكلّيّ المتوقّع من المكافآت الّتي يتلقّاها جرّاء اتّخاذه لإجراءٍ معيّنٍ في حالات البيئة، ومن الملاحظ تجاه الوكيل ليس رغبته بتعظيم المكافآت المباشرة الّتي يتلقّاها فحسب، وإنّما أيضًا المكافأة التّراكميّة الّتي سيتلقّاها لأجل المسار الكلّيّ، ولكن يفضّل في بعض الأحيان الحصول على مكافأةٍ صغيرةٍ في الخطوة الزّمنيّة التّالية من أجل الحصول على مكافأةٍ أعلى بمرور الوقت [4].

يمكن تمثيل عمليّة ماركوف لاتّخاذ القرار كمجموعةٍ (tuple) مؤلّفةٍ من أربعة عناصر وهي (S,A,Pa,Ra):

• S: يمثّل مجموعة من الحالات، ويحصل الوكيل في كلّ خطوةٍ زمنيّةٍ  t على تمثيلٍ لحالة البيئة  St، حيث أنّ  St ϵS.
• A: يمثّل مجموعة من الإجراءات الّتي يستطيع الوكيل اتّخاذها، ففي كلّ خطوةٍ زمنيّةٍ  t واعتمادًا على الحالة  St يقوم الوكيل بتنفيذ إجراءٍ  At حيث أنّ At∈A(St).
• Pa: يمثّل الاحتماليّة بأنّ إجراءٍ معيّنٍ في حالةٍ  s في خطوةٍ زمنيّةٍ  t ستنتج عنه الحالة  sَ في الخطوة الزّمنيّة t+1.
• Ra: أو بشكلٍ أدقٍ Ra(s,sَ) يمثّل المكافأة المتوقّعة المتلقّاة عقب الانتقال من حالة  s إلى حالة  sَ كنتيجةٍ لتطبيق الإجراء a [1].

2-3- معادلات بيلمان (Bellman Equations):

تعدّ معادلات بيلمان صنفًا من خوارزميّات التّعلّم المعزّز (RL) والّتي تستخدم بشكلٍ خاصٍّ في البيئات الحتميّة (deterministic environments)، وهي البيئات الّـتي تكون فيها النّتيجة_ بناءً على حالةٍ معيّنةٍ_ معروفةً وواضحةً بالنّسبة لنا مثل لعبة الشّطرنج (chess game) حيث أنّنا نعرف النّتيجة الدّقيقة لتحريك أيّ لاعبٍ فيها.

يتمّ تحديد قيمة حالةٍ معيّنةٍ V(s) من خلال أخذ الحدّ الأقصى من الإجراءات الّتي يمكننا اتّخاذها في الحالة (s) الّتي يكون فيها الوكيل، وذلك من أجل اختيار الإجراء (a) الّذي سيؤدّي إلى تعظيم قيمة الحالة V(s).

أي أنّ معادلة بيلمان باختصارٍ عبارةٌ عن إضافة المكافأة المباشرة الخاصّة بالإجراء الأمثل (a) المطبّق في الحالة (s) أي R(s,a) إلى عامل الخصم غامّا (Ƴ )_ الّذي يحدّد مدى اهتمام الوكيل بالمكافآت في المستقبل البعيد مقارنةً بتلك الموجودة في المستقبل القريب حيث تتراوح قيمته بين 0 و 1، القيمة المنخفضة منه تشجّع على المكافآت قصيرة الأمد في حين القيمة الأعلى منه تعدّ بمثابة مكافأةٍ طويلة الأمد_ مضروبًا بقيمة الحالة التّالية V(sَ)الّتي ينتقل إليها الوكيل نتيجة لتنفيذ الإجراء الأمثل  [4].

طبعًا من شأن هذه المعادلة تبسيط حساب دالّة القيمة (value function) ممّا يسمح لنا يإيجاد الحلّ الأفضل لمشكلةٍ معقّدةٍ، عن طريق تقسيمها إلى مشاكل فرعيةٍ صغيرةٍ يتمّ استدعاؤها بشكلٍ عوديٍّ وهذا ما توضّحه المعادلة التّالية [4]:

V(s)=max_a (R(s,a)+ƳV(sَ))

3-3- البرمجة الدّيناميكيّة (DP=Dynamic Programming):

ماذا لو واجهتنا مشكلة وجود فضاء حالاتٍ كبيرٍ وضخمٍ في أثناء استخدامنا لمعادلات بيلمان المثاليّة؟!
كيف يمكننا التّصرّف إزاء هذا السّيناريو الّذي من المحتمل فيه زيادة مستوى الصّعوبة، لدرجة القرب من الاستحالة في حلّ نظام المعادلات هذا بشكلٍ صريحٍ؟

هنا لابدّ لنا من الانتقال من نهج العوديّة (recursion) إلى نهج البرمجة الدّيناميكيّة (Dynamic Programming).

إذًا البرمجة الدّيناميكيّة واحدةٌ من طرق حلّ المشاكل من خلال تقسيمها إلى عدّة مشاكل فرعيّةٍ بسيطةٍ، وهنا في هذا النّهج سيتمّ تقدير قيمة كلّ حالةٍ من خلال إنشاء جدول بحثٍ خاصٍ بها [4].

يوجد لدينا خوارزميّتان في البرمجة الدّيناميكيّة تهتمّ بإيجاد السّياسة المثلى (optimal policy) وهما:

• تكرار القيمة (Value Iteration).
• تكرار السّياسة (Policy Iteration).

1-3-3- تكرار القيمة (Value Iteration):

سنقوم بداية بعرضٍ كاملٍ لخطوات الخوارزميّة من خلال الشّكل (2) المشار إليه في المرجع [5]، ومن ثمّ الانتقال مباشرًة لفهم التّفاصيل الكامنة بها لذلك لا يوجد داعٍ للقلق إزاء أيّ شيءٍ عزيزي القارئ:

كما نلاحظ فإنّه من المفترض لنا من أجل الدّخول في تكرارات الخوارزميّة_ بدءًا من السّطر 7 المشار إليه بحلقة (while)_استخدام عددٍ صغيرٍ θ (السّطر1) لمقارنته مع الفرق Δ المسند إليه قيمة  0 (السّطر 6)وتحديثه بشكلٍ مستمرٍّ ضمن الخوارزميّة (السّطر 11).

بشكلٍ مبدئيٍّ يتمّ تهيئة جميع قيم الحالات V(s) بشكلٍ كيفيٍّ ماعدا الحالة النّهائيّة حيث يتمّ إسناد قيمة الصّفر لها (السّطر 4+5)، بعد ذلك ستنفّذ الخوارزميّة بشكلٍ متكرّرٍ من أجل كلّ حالةٍ من فضاء الحالات  S (السّطر 8) لتسند القيم المخزّنة مسبقًا في V(s) إلى متحوّلٍ جديدٍ  V (لسهولة المقارنة بينهما) (السّطر 9)، ليتمّ بعدها تحديث قيم V(s) الأوّليّة باستخدام المعادلة السّابقة الّتي سنشير من خلالها لبعض الملاحظات (السّطر 10)، وهكذا إلى أن تصل القيم لحالة التّقارب (convergence) ونحصل في النّهاية على خرجٍ محتملٍ وهو السّياسة المثلى (optimal policy) الواجب اتّباعها بربط كلّ حالةٍ بالإجراء الأمثل فيها (السّطر 14)  [4].

بعض الملاحظات الجانبيّة المتعلّقة بالخوارزمّية:

1. من المعتاد تسمية خوارزميّة تكرار القيمة (Value Iteration) ب (معادلة بيلمان) بسبب ارتكازها واحتوائها على إحدى أشكال هذه المعادلة المتمثّلة بقيمة V(s)، وهذه الأشكال على اختلافها في المتغيّرات والمعاملات المستخدمة إلّا أنّ جميعها تساعد في تحديد السّياسة المثلى للوكيل من أجل أن يتّبعها في مشكلةٍ معيّنةٍ.
2. يمكن الإشارة إلى قيمة الحالة هنا ب  V*(s) كناية عن المكافأة الّتي يمكن أن أتوقّعها، فيما لو كنت في هذه الحالة وقمت باتّخاذ الإجراءات على النّحو الافضل المثاليّ.
3. قيمة الحالة بالقرب من حالاتٍ مزوّدةٍ بمكافأةٍ عاليةٍ ستكون أيضًا كبيرًة.
4. إنّ Σ يحسب القيمة المتوقّعة (expected value) لأنّنا في حالةٍ لاحتميّةٍ (non deterministic)، حيث عند اتّخاذ إجراءٍ ما  a قد ينتهي بنا المطاف إلى عددٍ من الحالات المختلفة  Sَ.
5. قد نصادف بدلًا من احتماليّة الانتقال  P في المعادلة، الرّمز T وهو كنايةٌ عن دالّة الانتقال من الحالة  s إلى الحالة التّالية  sَ وفق الإجراء  a.
6. الحدّ الأقصى (Max) هي للدّلالة على أنّنا نقوم بأخذ جميع الإجراءات الممكنة الّـتي نريدها، ولكنّنا نهتم فقط بالإجراء الّذي يمنحنا الحدّ الأقصى من المكافأة المتوقّعة في المستقبل (maximum future expected reward).
7. التّقارب (convergence) أي أنّ القيم لم تعد تتغيّر كثيرًا بعد تنفيذ المعادلة لعدّة آلافٍ من التّكرارات (iterations).
8. خوارزميّة تكرار القيمة (Value Iteration) تضمن التّقارب للقيم المثلى.
9. استخراج السّياسة (policy extraction) هي خطوةٌ منفصلةٌ، حيث بعد تطبيق خوارزميّة (value iteration) سنحتاج لاستخراج السّياسة من خلال استخدام معادلة بيلمان ذاتها باستثناء استبدال max ب argmax، ليتمّ ربط كلّ حالةٍ برقم فهرس الإجراء الأمثل لها ويشار لذلك بالرّمز π*.
10. يمكن الحصول على هذه السّياسة من خلال اختيار الإجراء الّذي من شأنه تعظيم دالّة قيمة الحالة المثلى (optimal state-value function) لحالةٍ ما، والّتي بدورها يمكن إيجادها باستخدام دالّةٍ تكراريّةٍ تسمّى تكرار القيمة (Value Iteration).

2-3-3- تكرار السّياسة (Policy Iteration):

تعمل هذه الخوارزميّة على مرحلتين:

• تقييم السّياسة (Policy Evaluation).
• تحسين السّياسة (Policy Improvement).

في البداية يبدأ وكيل التّعلّم المعزّز باختيار سياسةٍ كيفيّةٍ π  (السّطر 5) في الشّكل (3)– عبارةٌ عن جدولٍ بأزواج (حالة وإجراء) أي يتمّ ربط كلّ حالةٍ بإجراءٍ معيّنٍ بشكلٍ كيفيٍّ- ثمّ بشكلٍ متكرّرٍ يُقيّم ويُحسّن السّياسة اعتمادًا على مرحلة (Policy Evaluation) و مرحلة (Policy Improvement) حتّى الوصول لحالة التّقارب (convergence).

يتمّ تقييم السّياسة من خلال احتساب دالّة قيمة الحالة (state value function) أي V(s)(السّطر 9)  في الشّكل (3) وفق المعادلة التّالية (معادلة بيلمان) الّتي سبق وأن قمنا بشرحها ولكن بفارقٍ إضافيّ هنا هو اعتمادنا على استخدام  السّياسة الأوّليّة الّتي قمنا بتهيئتها بشكلٍ عشوائيٍّ  Π(s) في حساب قيمة الحالة V(s) بدلًا من اختيار الإجراء الّذي يعظّم من هذه القيمة  [5]:

V(s)=Σ_sَ,rp(sَ,r|s,Π(s))[r+ ϒV(sَ)]

بعد مرحلة التّقييم، تأتي مرحلة حساب السّياسة المحسّنة وذلك من أجل استبدال السّياسة الأوّليّة π الّتي تمّ تخزينها في متحوّلٍ جديدٍ (old-action) (السّطر 15) في الشّكل (3)  وهذا وفق المعادلة التّالية، حيث يتمّ الاستفادة من النّتائج الّتي حصلنا عليها في مرحلة تقييم السّياسة من أجل احتساب القيم لكلّ إجراءٍ ممكنٍ (a) في الحالة (s) ليتمّ عندها اختيار أعلى قيمة من بين النّتائج وربط الإجراء الخاصّ بها بالحالة (s)، وذلك باستخدام دالّة (argmax):

Π(s)=argmax_a Σ_sَ,rp(sَ,r|s,a)[r+ϒV(sَ)]

في البداية لا نهتمّ كثيرًا بالسّياسة الأوّلية π0 بكونها أمثليًّة أم لا، حيث أنّنا خلال التّنفيذ نركّز على تحسينها في كلّ تكرارٍ من خلال تكرار مرحلة تقييم السّياسة المتمثّلة بالرّمز E  ومرحلة تحسين السّياسة المتمثّلة بالرّمز I، وهكذا سنلاحظ فيما بعد  من خلال الشّكل (4) أنّنا في النّهاية نقوم بإنتاج سلسلةٍ من السّياسات حيث أنّ كلّ سياسةٍ ماهي إلّا تحسينٌ لسابقتها من أجل الوصول في النّهاية إلى سياسةٍ مثلى π * وقيمٍ مثلى V* (السّطر 21) في الشّكل (3).

سيتمّ الاستمرار بإجراء هاتين المرحلتين إلى حين الوصول لحالة الاستقرار وعدم تحسّن السّياسة بعد ذلك (وإلّا يجب علينا العودة لمرحلة تقييم السّياسة (Policy Evaluation) (السّطر 23)) في الشّكل (3)، وهكذا نحصل في النّهاية على خرجٍ متمثّلٍ بدالّة القيمة المثلى (optimal value function) و سياسةٍ مثلى أيضًا (optimal policy)،  وهذا ما توضّحه خطوات الخوارزميّة في الشّكل (3):

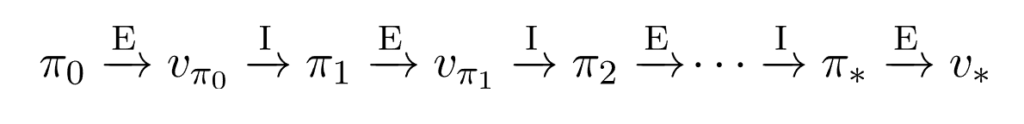
يمكننا إجراء تلخيصٍ بأهمّ الفوارق بين الخوارزميّتين السّابقتين وفق الجدول (1):

Value Iteration	Policy Iteration
تبدأ بدالّة قيمٍ عشوائيّةٍ (random value function).	تبدأ بسياسةٍ عشوائيّة (random policy).
الخوارزميّة بسيطة	الخوارزميّة أكثر تعقيد.
تضمن التّقارب.	تضمن التّقارب.
مكلفةٌ أكثر من أجل الحساب.	أقلّ تكلفةٍ في الحساب.
تتطلّب تكراراتٍ أكثر من أجل التّقارب.	تتطلّب تكراراتٍ أقلّ من أجل التّقارب.
خوارزميّةٌ بطيئةٌ.	خوارزميّةٌ سريعةٌ.

معضلة الاستكشاف (Exploration) والاستغلال (Exploitation) في التّعلّم المعزّز:

لابدّ لنا عند الحديث عن التّعلّم المعزّز وخوارزميّاته، من التّطرّق بشكلٍ أساسيٍّ لمعضلة الاستكشاف والاستغلال الّتي ترد كثيرًا من دون معرفة الفرق الرّئيسيّ بين المصطلحين.

بالطّبع يوجد الكثير من التّعاريف حول هذا الموضوع، وسنقوم بصياغة وتلخيص الفرق كالتّالي [6]:

جميعنا نحن البشر بشكلٍ عامٍ نعتمد على تجربة الأشياء ببساطةٍ من أجل التّعرّف على العالم المحيط بنا وفهم ما يدور حولنا، وهنا تكمن المشكلة بين اختيار مانعرفه للحصول على شيءٍ قريبٍ  ممّا نتوقّع (Exploitation) وبين اختيار شيءٍ لسنا متأكّدين البتّة حوله وربّما من المحتمل أن نتعلّم المزيد عنه (Exploration).

أي يمكن اعتبار الاستغلال كنهجٍ جشعٍ (greedy) يحاول فيه الوكيل أن يحصل على مزيدٍ من المكافآت بالاعتماد على القيمة المقدّرة وليس على القيمة الفعليّة، وبالتّالي يتّخذ الوكيل القرار الأفضل بناءً على معلوماته الحاليّة، على عكس تقنيّة الاستكشاف حيث فيها يركّز الوكيل على تحسين معرفته حول كلّ إجراءٍ بدلًا من الحصول على مزيدٍ من المكافآت من أجل أن يتمكّن من الحصول على منافع طويلة الأمد (long-term) وقرارٍ أفضل شاملٍ [6].

الخاتمة:

إنّ التّعلّم المعزّز واحدٌ من أكثر الأجزاء إفادة ومتعة في مجال تعلّم الآلة (Machine Learning)، حيث تمّ التّركيز في هذا المقال على معادلات بيلمان الشّهيرة (Bellman Equations) لما لها من أهميّة في إعطائنا القدرة على حساب قيمة حالةٍ معيّنةٍ ومساعدتنا باتّخاذ القرار الأمثل والأفضل بها من أجل إيجاد القيمة المثلى V* والسّياسة المثلى π *، وهذا ما تسعى لتقديمه البرمجة الدّيناميكيّة (DP) بفرعيها تكرار القيمة (Value Iteration) و تكرار السّياسة (Policy Iteration).

ويفيض النّبع بهذه الخوارزميّات ولا ينضبُ، لذلك سنتابع في مقالتنا اللّاحقة مناقشة البعض الآخر منها، مع الانتباه على أنّه لسنا ملزمين دائمًا بتوصيف وحلّ أيّ مشكلةٍ وفق التّعلّم المعزّز (فقد تكون خوارزميّات تعلّم الآلة الأخرى أكثر فاعليّةً وكفاءةً منها) وخاصّةً إذا كانت لدينا بيانات كافية لحلّها.

المراجع:

1. Guide to Reinforcement Learning with Python and TensorFlow
2. Reinforcement Learning Tutorial – Javatpoint
3. Introduction to Various Reinforcement Learning Algorithms. Part I (Q-Learning, SARSA, DQN, DDPG) | by Kung-Hsiang, Huang (Steeve) | Towards Data Science
4. Deep Reinforcement Learning: Definition, Algorithms & Uses
5. Value Iteration vs. Policy Iteration in Reinforcement Learning | Baeldung on Computer Science.
6. What is Exploration vs. Exploitation in Reinforcement Learning? | by Angelina Yang | Medium
7. نظرة عامة على التعلُّم المُعزَّز Reinforcement Learning – الذّكاءُ الإصطناعيُّ باللُّغةِ العربيّةِ
8. قاموس المُصطلحات العلميّة – الذّكاءُ الإصطناعيُّ باللُّغةِ العربيّةِ