تهيئة الشبكات العصبونيّة

إن تهيئة أوزان الشبكات العصبونية العميقة له تأثير كبير على التقارب أثناء عملية التدريب، ومن الجدير بالذكر أنه ولزمن ليس بالبعيد قبيل عام ٢٠٠٦ لم تكن عملية تدريب الشبكات العميقة تتم بشكل ناجح ويرجع ذلك لسوء اختيار وتهيئة توابع التفعيل (٢). لحل هذه المشكلة تم إيجاد العديد من مخططات التهيئة البسيطة لتسريع عملية التدريب لكنها تتطلب بعض الحذر لتجنب الأخطاء الشائعة. وسنقوم في هذه المقالة بشرح كيفية تهيئة معاملات الشبكة العصبونية بشكل فعّال.

أهمية التهيئة الفعّالة

عند البدء ببناء خوارزمية تعلم آلة، عادة ما نبدأ بتحديد بنية لهذه الخوارزمية ( الانحدار اللوجستي Logistic regression، آلة متجه الدعم Support Vector Machine، الشبكة العصبونية) ومن ثم تدريبها على تعلم المعاملات. تتم عملية التدريب الشائعة للشبكة العصبونية  بالخطوات التالية:

1- تهيئة المعاملات
2- اختيار خوارزمية التحسين المناسبة
3- تكرار الخطوات التالية:

• التغذية الأمامية للدخل Forward propagate an input
• حساب تابع الكلفة
• حساب مشتقات الكلفة بالنسبة للمعاملات باستخدام الانتشار العكسي.
• تحديث كل معامل باستخدام المشتقات وفقًا لخوارزمية التحسين.

بعد ذلك، ومن خلال إعطاء عينة بيانات جديدة يمكن استخدام النموذج لتوقع الصنف.

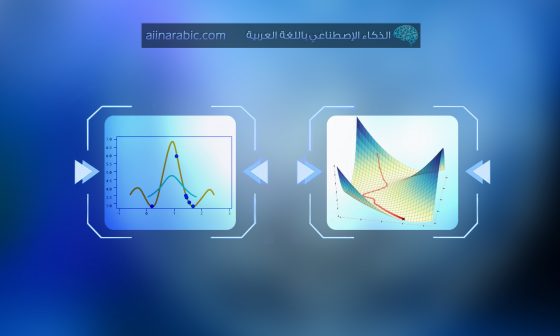
يمكن لعملية التهيئة أن تحدد مدى سرعة تقارب الشبكة وما إذا كانت تتقارب أم  لا. وعلى الرغم من أن عملية ضبط الأوزان ليست سوى معامل واحد من بين العديد من المعاملات التي يجب ضبطها إلا أن توزيعها يؤثر بشكل كبير على المشتقات وبالتالي فعالية التدريب. بناء على ذلك، يجب التأكد من ضبط المعاملات بالطريقة الصحيحة  لأنها ستكون حاسمة في أداء النموذج النهائي. ولتوضيح ذلك،  نشر موقع Deeplearning.ai مؤخرًأ منشوراً تفاعلياً يعطينا حرية اختيار أساليب تهيئة مختلفة لشبكة عصبونية ذات ثلاث طبقات ويعرض مدى تأثير اختلاف هذه المعاملات على تدريب الشبكة. وذلك كما في الشكل (1).

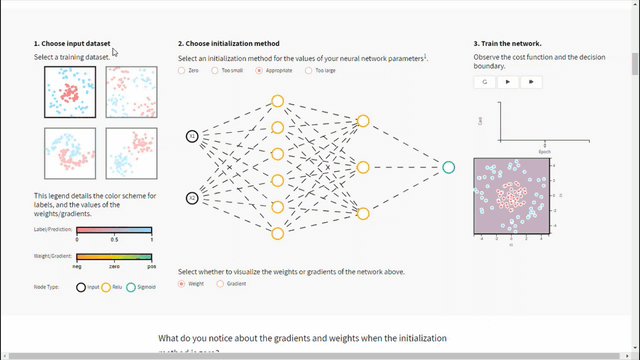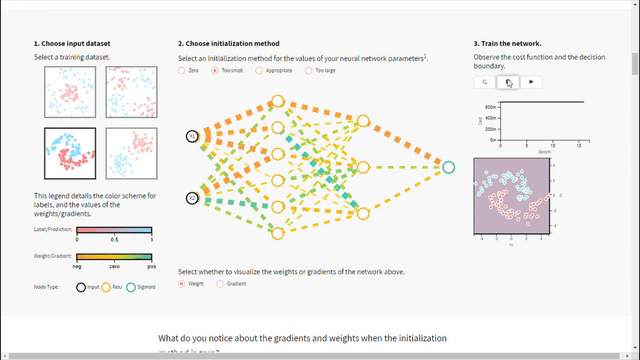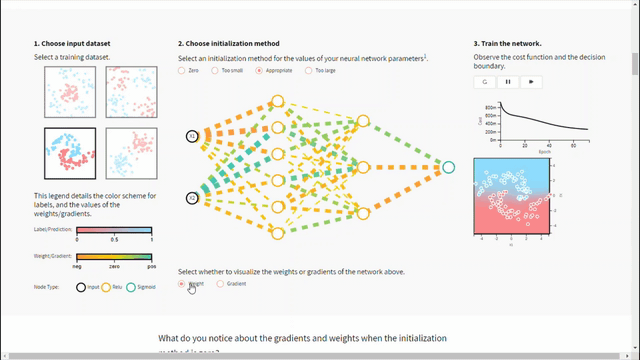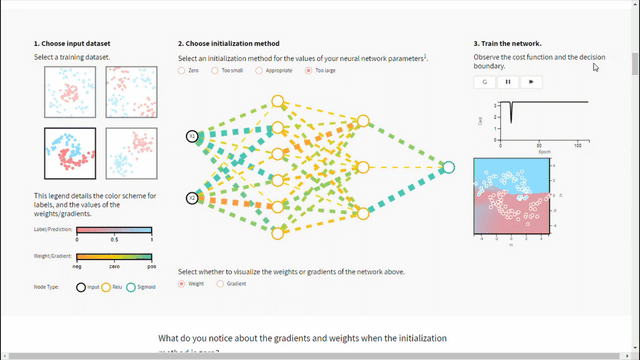
– ما تأثير جعل المعاملات مهيأة بصفرعلى الأوزان والمشتقات؟
إنّ تهيئة جميع الأوزان بقيمة صفر تجعل العصبونات تتعلم نفس المزايا خلال التدريب، فكيف ذلك؟
بشكل عام إن تهيئة معاملات الشبكة بقيم ثابتة سوف يؤدي إلى أداء ضعيف جدًا. فعلى فرض أنه لدينا شبكة عصبونية تحوي وحدتان خفيتان وقمنا بتهيئة كل الانحيازات biases بالقيمة صفر والأوزان بقيمة ثابتة  ألفا a. وعند التغذية الأمامية للدخل (x1,x2) في هذه الشبكة سيكون خرج كلا من الوحدتين الخفيتين relu(ax1+ax2) أي سيكون لكلا الوحدتين التأثير نفسه على الكلفة بالتالي الحصول على مشتقات متماثلة ويتطور كلا من العصبونين بشكل متناظر طوال التدريب. مما يمنع العصبونات المختلفة من تعلم أشياء مختلفة.

– ما تأثير تهيئة الأوزان بقيمة صغيرة أو كبيرة جدًأ على مخطط الكلفة؟
على الرغم من تجاوز مشكلة تماثل قيم المعاملات إلا أن تهيئة الأوزان بقيم صغيرة جدًا أو كبيرة جدًأ سيؤثر سلبًا على عملية التدريب من خلال المساهمة في خلق مشكلة تلاشي أو تضخم المشتقات. فعند تحديث الأوزان بقيم صغيرة جدًا سيجعل  عملية التقارب وتحسين تابع الخسارة بطيئة  و بأسوء الحالات بالتالي قد يؤدي إلى تلاشي المشتقات. وعلى العكس فعند تهيئة الأوزان بقيم كبيرة جدًا ستسبب مشكلة تضخم المشتق والتي تتمثل بتراكم مشتقات الأخطاء الكبيرة  تحديثات كبيرة لأوزان نموذج الشبكة العصبية خلال التدريب. مما يجعل النموذج غير مستقراً وغير قادراً على التعلم من بيانات التدريب.
لذلك فإنّ اختيار القيم المناسبة للتهيئة ضروري جدًا للتدريب الفعّال. عزيزي القارئ سنتحقق من هذا الأمر بشكل أكبر في القسم التالي.

مشكلة تضخم أو تلاشي المشتقات exploding or vanishing gradients

لنفترض الشبكة العصبونية التالية المكونة من تسع طبقات.

في كل تكرار لحلقة التحسين (التغذية الأمامية، حساب الكلفة، التغذية العكسية، التحديث) نلاحظ بأن مشتقات الانتشار العكسي إما تم تضخيمها أو تصغيرها عند الانتقال من طبقة الخرج باتجاه طبقة الدخل. إن هذه النتيجة منطقية عند التفكير في المثال التالي:
على فرض أن جميع توابع التفعيل هي خطية (التابع الواحدي- identity function)عندها خرج التابع سيكون:

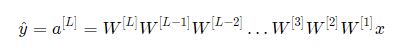
حيث   جميعها مصفوفات بأبعاد (2,2) لأن جميع الطبقات من 1 إلى L-1 تحوي عصبونين وتستقبل دخلين. ولتسهيل توضيح الفكرة سنفرض أن جميع هذه المصفوفات متساوية أي عندها تنبؤ الخرج سيكون:

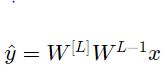
بناء على ما سبق كيف ستكون نتيجة قيم التهيئة التي كانت صغيرة جدًا أو كبيرة جدًا أو مناسبة؟

1- قيم التهيئة الكبيرة جدًأ والتي ستؤدي إلى تضخم المشتق

على فرض تم تهيئة جميع الأوزان بقيم أكبر بقليل من المصفوفة المعرفة السابقة.كما في الشكل:

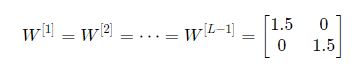
 أو يمكن تبسيطها لتصبح:

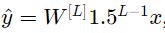
حيث أن قيمة (ناتج تابع التفعيل)  تزداد بشكل أسي مع L. و باستخدام قيم توابع التفعيل هذه في الانتشار العكسي سنواجه مشكلة تضخم المشتق. أي يحدث تضخم المشتق نتيجة تكرار ضرب المشتقات عبر طبقات الشبكة بقيم أكبر من 1.0.
بالتالي أصبحت مشتقات الكلفة بالنسبة إلى المعاملات كبيرة جدًأ مما يؤدي إلى تذبذب الكلفة حول قيمتها الصغرى.

2- قيم التهيئة الصغيرة جدًأ والتي ستؤدي إلى زوال المشتق

بشكل مشابه، لنفترض تهيئة كل الأوزان بقيم أصفر بقليل من المصفوفة المعرّفة. 

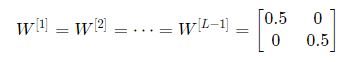
وبشكل مختصر يعبر عنها بالشكل:

وقيمة تابع التفعيل تتناقص بشكل أسي مع L. وعند استخدامنا قيم توابع التفعيل هذه في الانتشار العكسي نواجه مشكلة تلاشي المشتق. وهذا يعني أن مشتقات الكلفة بالنسبة إلى المعاملات صغيرة جدًا مما يؤدي إلى تقارب الكلفة قبل وصولها القيمة الصغرى.
وبشكل عام، فإنّ تهيئة الأوزان بقيم غير مناسبة سيؤدي إلى اختلاف أو تباطؤ تدريب الشبكة العصبونية. على الرغم من إيضاح مشكلتي  تضخم و تلاشي المشتق مع مصفوفات أوزان متناظرة بسيطة إلا أن النتائج تعمم على أي قيم تهيئة كبيرة كانت أو صغيرة جدًا.

3-  كيف يمكن إيجاد قيم تهيئة مناسبة؟

لمنع مشتقات توابع تفعيل الشبكة من التلاشي أو التضخم، يجب الالتزام بالقواعد التالية:
1- المتوسط الحسابي للتفعيل يجب أن يكون صفر.
2- تباين تابع التفعيل يجب أن يبقى نفسه عبر كل الطبقات.
بموجب هذين الافتراضين لا يجب ضرب إشارة مشتق الانتشار العكسي بقيم صغيرة أو كبيرة جدًا في أي طبقة. يجب أن تنتقل إلى طبقة الدخل دون حدوث تلاشي أو تضخم. وبشكل أكثر تحديدًا، لنفترض الطبقة L وترسل بالانتشار الأمامي مايلي:

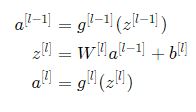
حيث تمثل الدخل إلى الطبقة L و تمثل الخرج. يمثل تابع التفعيل في الطبقة L. بينما  يمثل عدد العصبونات في الطبقة L.

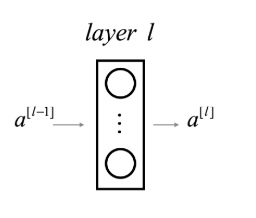
ونريد إثبات ما يلي:

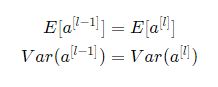
حيث E تمثل المتوسط و Var تمثل التباين وعليه يجب ضمان بقاء قيمة المتوسط صفرية و قيمة تباين الدخل لكل طبقة بدون تضخم أو تلاشي. هذه الطريقة تطبق على كلٍ من الانتشار الأمامي وذلك لتوابع التفعيل وعلى  الانتشار العكسي لمشتقات الكلفة بالنسبة لتوابع التفعيل. اإنّ التهيئة الموصى بها هي تهيئة كزافير Xavier أو أي طريقة مشتقة منها لكل طبقة.

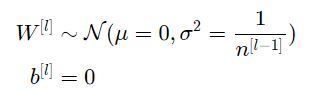
أي كل أوزان الطبقة L تهيئ بشكل عشوائي من تابع التوزيع الطبيعي بمتوسط حسابي مساوي للصفر وانحراف مساوي لـ  حيث تمثل عدد العصبونات في الطبقة L-1 وأخيرًأ يتم تهيئة الانحياز بالقيمة صفر.
يوضح التمثيل التالي تأثير تهيئة كزافير على تفعيل كل طبقة في شبكة عصبونية ذات خمس طبقات كاملة الاتصال.

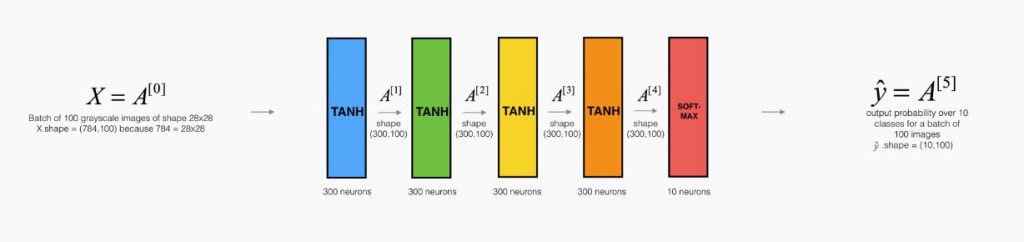
يوضح القسم التالي التبرير الرياضي لتهيئة كزافيير ويشرح بشكل أدق لما يعتبر أسلوب تهيئة فعّال.

التبرير الرياضي لتهيئة كزافيير Xavier

سنرى كيف أن كزافيير يحافظ على قيمة التباين عبر جميع الطبقات. سنفترض بأن توابع تفعيل الطبقات سيتم توزيعها بشكل طبيعي حول الصفر. أحيانًا فهم البرهان الرياضي يساعد على زيادة استيعاب الفكرة ولكن أيضًا يمكن فهم الفكرة الأساسية بدون الرياضيات.
لنقوم بالعمل على الطبقة L المعرفة في الفقرة السابقة الشكل (2) ونفترض أن تابع التفعيل هو tanh. عندها سيكون الانتشار الأمامي هو:

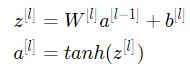
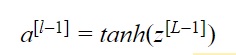
الهدف هو إيجاد العلاقة بين تباين تابع تفعيل الطبقة L-1 والطبقة L. عندها سنفهم كيفية تهيئة الأوزان بالشكل الذي يحقق تساوي التباين في كلا الطبقتين L وL-1.
على فرض أنه تم تهيئة الشبكة بالقيم المناسبة وتم توزيع الدخل بشكل طبيعي. في بداية التدريب سنكون في المجال الخطي لتابع التفعيل tahn. والقيم صغيرة كفاية أي الظل للقيمة مساوي للقيمة نفسها  وذلك يعني أن التباين عند هذه القيمة هو نفسه تباين قيمة تابع التفعيل
وأيضًا:

حيث:

وللتبسيط: نفترض  أن  الانحيازات صفرية  . و باخذ ال element-wise  للمعادلة السابقة  (تباين الشعاع هو نفسه تباين أي من مدخلاته. لأن كل المدخلات ترسم بشكل مستقل ومن نفس التوزيع أي:

بالتالي نكتب:

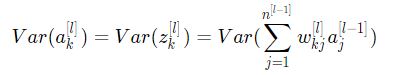
 لتبسيط المعادلة السابقة يمكننا تطبيق حيلة رياضية وهي إخراج عملية الجمع خارج التباين وللقيام بذلك يجب أن تكون الفرضيات الثلاث  التالية محققة:
1- الأوزان مستقلة وموزعة بالتساوي
2- قيم الدخل مستقلة وموزعة بالتساوي
3- الأوزان وقيم الدخل مستقلة عن بعضها البعض
بهذا يصبح لدينا:

والحيلة الرياضية الثانية المطبقة هي تحويل تباين جداءات إلى جداء تباينات باستخدام الصيغة التالية(صحيحة فقط من أجل المتحولات الموزعة عشوائيًا)

باستخدام هذه العلاقة مع فرض أن:  ستصبح العلاقة:

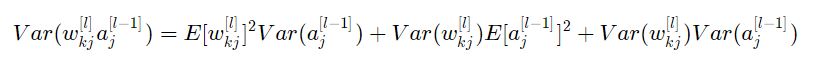
تقريبًأ انتهينا! أول افتراض أدى إلى أن والافتراض الثاني أدى إلى كون أن جميع الأوزان مهيأة بمتوسط صفري والدخل موزع بشكل طبيعي بالتالي:

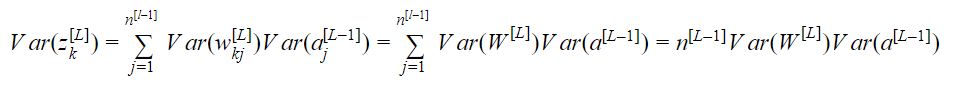
نتجت المعادلة السابقة من الافتراض  الأول:

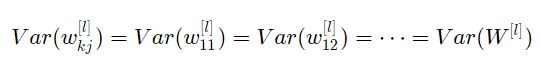
وبشكل مشابه الافتراض الثاني أدى إلى:

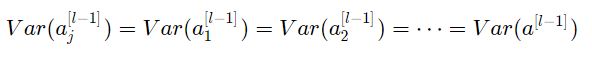
وبنفس الفكرة

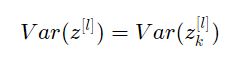
و بدمج كل شيء معًا

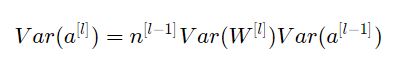
عظيم إذاً  لجعل التباين متساوي عبر جميع الطبقات

يجب أن يكون:
هذا يبرر اختيار التباين لتهيئة كزافير.
لم يتم اعتماد طبقة محددة في العمليات السابقة بالتالي هذا التعبير يعمل على جميع طبقات الشبكة . على فرض L هي طبقة خرج شبكتنا باستخدام هذا التعبير عند كل طبقة يمكن الربط بين تباين طبقة الخرج مع تباين طبقة الدخل بالشكل التالي:

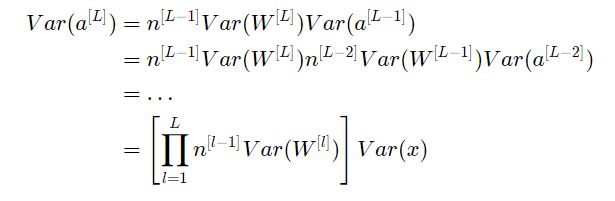
اعتمادًا على كيفية تهيئة الأوزان ستختلف العلاقة بين تباين الخرج والدخل بشكل كبير وسنكون أمام إحدى الحالات التالية:

بالتالي من أجل تجنب تلاشي أو تضخم الإشارة المنتشرة أماميًأ يجب ضبط:

من خلال تهيئة

عملنا في التبرير الرياضي  على التفعيل الناتج من الانتشار الأمامي. يمكن الحصول على نفس النتيجة  من مشتقات الانتشار العكسي  وحينها  من أجل تجنب تلاشي أو تضخم المشتقات يجب ضبط:

من خلال تهيئة 

بهذا نكون قد شرحنا التبرير الرياضي النظري لتهيئة كزافيير الذي يعمل مع تابع التفعيل tahn. وهناك العديد من الطرق الأخرى المستخدمة في عملية التهيئة كما ذكرنا سابقًأ. فمثلًأ في حال كان تابع التفعيل المستخدم هو ريلو ReLU عندها التهيئة الشائعة المستخدمة هي (He et al., Delving Deep into Rectifiers) حيث يتم فيها تهيئة الأوزان بضرب تباين تهيئة كزافيير بالقيمة 2. و التبرير الرياضي لعملية التهيئة هذه يتم بنفس الطريقة المتبعة في tahn لكن بتعقيد أكبر بقليل.

الخاتمة

تعرفنا في هذا المقال على الأثر الكبير لتهيئة المعاملات على تدريب الشبكة وفعالية النموذج النهائي. ومنه تعلمنا كيف تتم عملية التهيئة بالشكل الصحيح لتجنب مشكلة تضخم أو تلاشي المشتق التي قد تحدث عند التهيئة بقيم كبيرة أو صغيرة جدًا.

وشرحنا إحدى الطرق المستخدمة في عملية التهيئة وهي كزافيير الذي يعمل مع تابع التفعيل tahn ويستخدمها مهندسو تعلم الآلة إمّا لتهيئة الأوزان كـ أو كـ  عندها يكون التباين للتوزيع الأخير هو المتوسط التوافقي لـو.

المراجع

[1]-Selecting the right weight initialization for your deep neural network
[2]-Xavier Glorot Yoshua Bengio, DIRO, Universite de Montr ´ eal, Montr ´ eal, Qu ´ ebec, Canada, “Understanding the difficulty of training deep feedforward neural networks”, 2010.
[3]-Learning Process of a Deep Neural Network
[4]-A Gentle Introduction to Exploding Gradients in Neural Networks
[5]-An Explanation of Xavier Initialization
[6]-Initializing neural networks