الشبكة العصبونية الكثيفة DenseNet

مقدمة

حققت الشبكات العصبونية العميقة Deep Neural Networks التي أضافت إلى طبقاتها بما يُعرف وصلة تخطّي skip-connection نتائج رائعة في السنوات الأخيرة واعُتبرت الشبكة العصبونية الكثيفة DenseNet قائمة على هذه المبدأ لكن بأسلوب آخر باعتمادها أسلوب اتصال جديد بين الطبقات. كما هو معروف أن الشبكات العصبونية الأعمق هي الأكثر كفاءة مقارنة مع الشبكات العصبونية الواسعة التي قللت من الكلفة الحسابية وزمن التدريب ولكن أيضاً يبقى أداء الشبكات العصبونية العميقة محدود بسبب مشكلة تلاشي المشتق Vanishing Gradient وبالاضافة إلى أنه مكلفة حسابياً جداً وتحتاج إلى وقت تدريب طويل إلى أن أتت الشبكات العصبونية الكثيفة وحققت نتائج رائعة جداً عن طريق الجمع بين مزايا العمق والعرض. قُدمت معمارية الشبكة العصبونية الكثيفة من قبل المؤلفون هوانغ ورفاقه في ورقتهم البحثية المنشورة في العام 2017 والتي حصلت على جائزة أفضل ورقة بحثية في مؤتمر الرؤية الحاسوبية والتعرف على النماذج Conference on Computer Vision and Pattern Recognition 2017 وعالجت هذه المعمارية مشاكل التدريب التي تحصل عند زيادة عمق الشبكة العصبونية.

بنية الشبكة العصبونية الكثيفة DenseNet Architicture

في شبكات الطَّي العصبونية الاعتيادية Convolutional Neural Network يكون الدخل عبارة عن صورة وتتدفق بيانات هذه الصورة عبر طبقات الشبكة العصبونية من الطبقة الأولى تليها الطبقة الثانية وهكذا بالتسلسل حتى الطبقة الأخيرة التي يتم التنبؤ عندها بخرج الشبكة المتوقع Predicted class. كما هو موضح في الشكل 1.

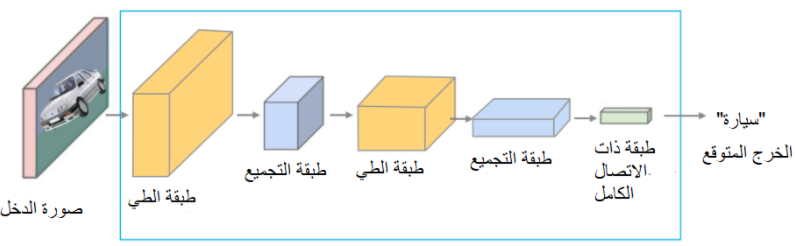
كما رأينا في الشكل 1 آلية الاتصال بين طبقات شبكة الطَّي العصبونية الاعتيادية حيث تنتج كل طبقة خرائط المزايا Feature Maps والتي تعد دخل للطبقة التي تليها بعبارة اخرى يكون خرج كل طبقة هو دخل للطبقة التالية باستثناء الطبقة الاخيرة التي تنتج الخرج المتوقع وبالتالي من أجل عدد من الطبقات وليكن L يكون لدينا اتصال مباشر بين الطبقات بعدد هذه الطبقاتL، أما بالنسبة للشبكة العصبونية الكثيفة فقد اعتمدت طريقة اتصال جديدة بين الطبقات بحيث تتصل جميع الطبقات مع بعضها البعض بشكل مباشر كما هو موضح في الشكل 2.

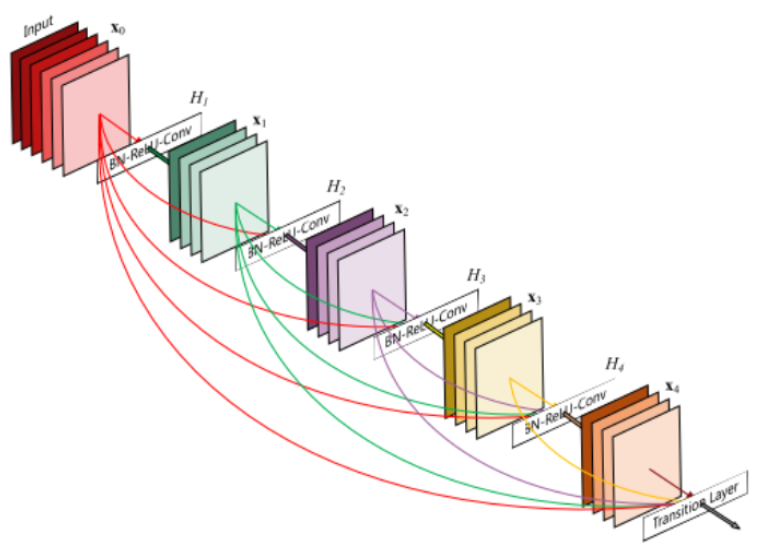
الشكل 2 يمثل آلية الاتصال بين طبقات الشبكة العصبونية الكثيفة نلاحظ أن دخل كل طبقة هو عبارة عن خرائط المزايا لجميع الطبقات السابقة لها، وخرج كل طبقة هو دخل لجميع الطبقات التي تليها. وبالتالي من أجل عدد من الطبقات وليكن L يكون لدينا عدد الاتصالات المباشرة بين الطبقات هو L(L+1)/2، وهذه كانت الفكرة الرئيسية وراء معمارية الشبكة العصبونية الكثيفة.
الآن نحن علمنا أن دخل الطبقة L_th هو سلسلة من خرائط المزايا للطبقات السابقة L₁ ,L₂ ,…..L_th-1 ونعلم أيضاً أن أبعاد خرائط المزايا تتغير من طبقة لطبقة في الشبكة ولا يبقى حجمها ثابت خلال طبقات الشبكة. إذاً السؤال الأبرز هنا، إذا كان حجم خرائط المزايا يتغير باستمرار هل من الممكن تجميع خرائط المزايا هذه مع بعضها البعض؟ إذا كان من الممكن كيف؟ إذا كان غير ممكن فماذا ينبغي علينا لنجعل هذا الأمر ممكن؟

إن الجزء الرئيسي من طبقات شبكات الطّي العصبونية هي طبقات تصغير الأبعاد Downsampling والتي تتولى مهمة تصغير أبعاد خرائط المزايا، كما يوضح الشكل 3 نستطيع الملاحظة بوضوح تغير أبعاد خرائط المزايا في شبكة الطّي في جي جي VGG الأمر الذي يجعل عملية تجميع خرائط المزايا في هذه الحالة غير ممكنة نظراً لامتلاك خرائط المزايا احجام مختلفة.

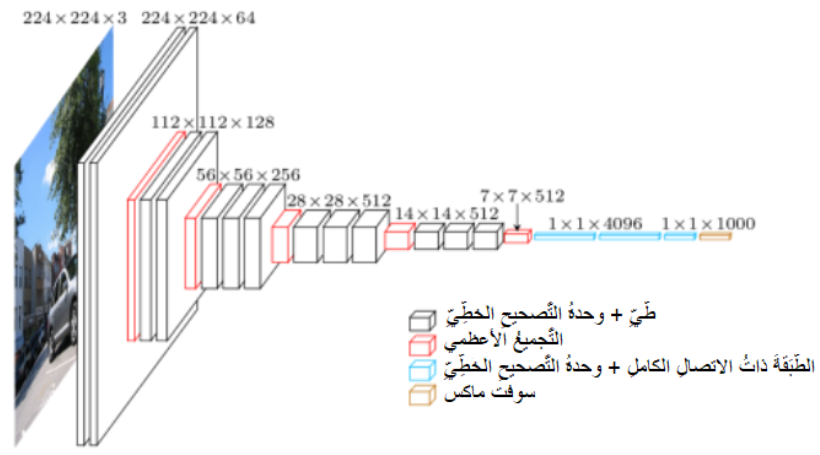
حيث يكون بُعد الدخل في شبكة في جي جي 3×224×224 إلى أن يصبح في النهاية  512×7×7.
ولحل مشكلة اختلاف أبعاد خرائط المزايا من أجل إجراء عملية التجميع، اقترح المؤلفون هوانغ ورفاقه تقسيم الشبكة العصبونية إلى كتل كثيفة Dense Block، بحيث تبقى أبعاد خرائط المزايا ثابتة داخل الكتلة، مما يجعل عملية تجميع خرائط المزايا ممكناً.

ويتم إجراء عمليات الطَّي والتجميع Pooling خارج الكتل الكثيفة وهذا ما يمكننا من إجراء عملية تصغير الأبعاد التي لا بد منها في شبكات الطّي العصبونية سنرى لاحقاً أين تتم كلاً من عملية الطَّي والتجميع.

الكتلة الكثيفة Dense Block

كما ذكرنا سابقاً، أن الشبكة العصبونية الكثيفة مقسمة إلى كتل كثيفة وأن كل كتلة يتم تحقيق الاتصال الكامل فيها أي دخل كل طبقة هو خرج جميع الطبقات السابقة. يتم تمثيل الاتصال الكامل بالمعادلة التالية:

x_L = H_L([x₀, x₁ …. , x_L-1])

حيث:

 H: يمثل التحول غير الخطي non-linear transformation المطبق على الطبقة l.

 x: خرج الطبقة.

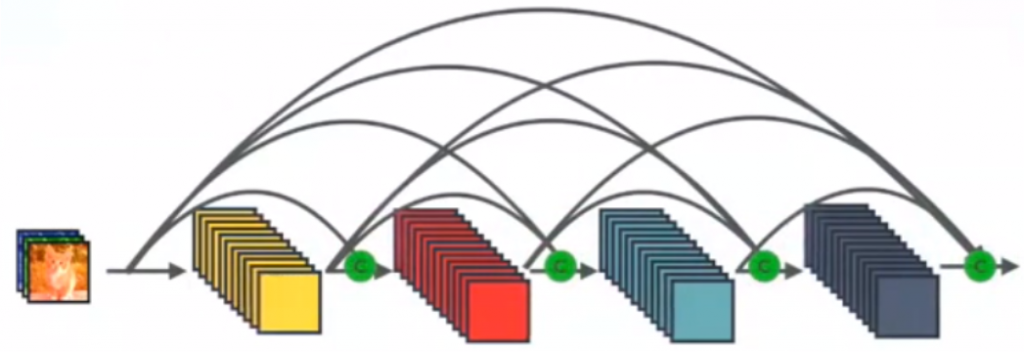
من أجل كل طبقة داخل الكتلة الكثيفة يتم تطبيق الدالة المركبة Composite Function والتي تتألف من ثلاث عمليات متتالية هي:

1. تقييسُ الدُّفعَةِ Batch Normalization.
2. تابع التفعيل وحدةُ التَّصحيحِ الخطِّيِّ Relu.
3. طَّي باستخدام مرشح ببُعد 3×3.

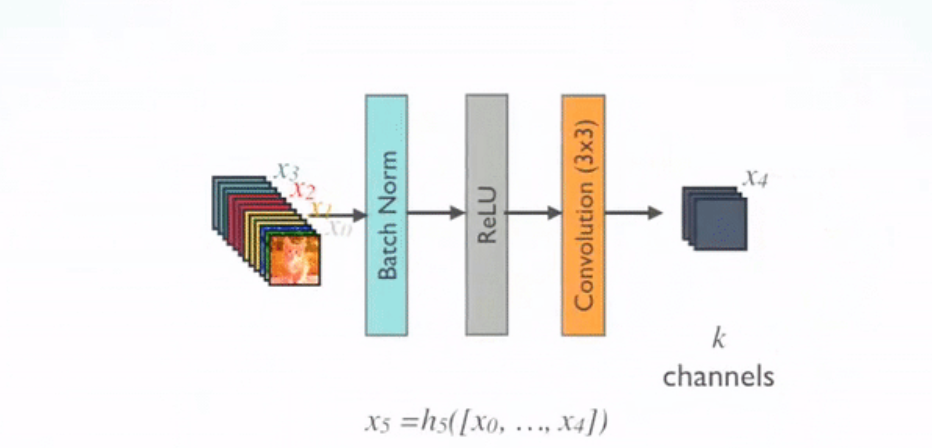
وجد هوانغ ورفاقه أن تطبيق تابع التفعيل (وحدةُ التَّصحيحِ الخطِّيِّ) قبل عملية الطَّي 3×3 يعطي نتائج أكثر فاعلية من تطبيقه بعد عملية الطَّي 3×3. كما أوصى المؤلفون بإجراء حشوُ صفري  Zero Padding قبل عملية الطَّي من أجل الحفاظ على الأبعاد نفسها.

طبقات الانتقال Transition Layers

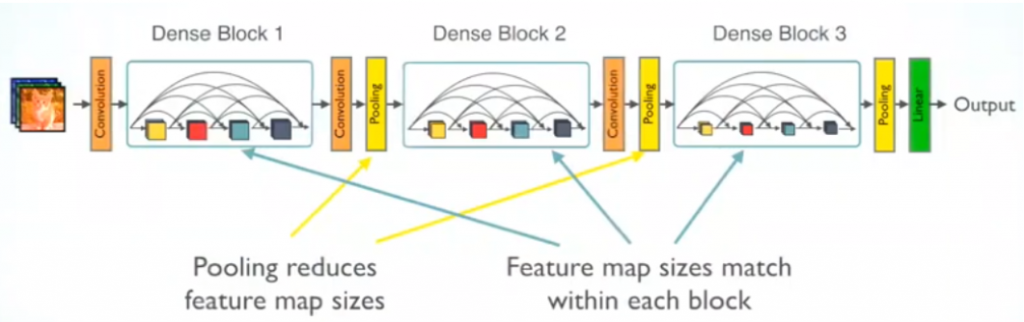
كما رأينا سابقاً أنه يتم إجراء عملية الحشو الصفري من أجل الحفاظ على أبعاد خرائط المزايا داخل الكتلة الكثيفة، ولكن في شبكات الطَّي العصبونية تصغير أبعاد خرائط المزايا هو أمر مهم وضروري ولا بد منه كما تحدثناً منذ قليل ولهذا لابد من أجراء عملية تصغير الأبعاد. وكما ذكرنا سابقاً أن إجراء عملية تصغير الأبعاد داخل الكتلة الكثيفة أمر غير وارد ولا يمكن إجراءها من أجل الحفاظ على أبعاد خرائط المزايا لذلك تم اقتراح إجراء عملية تصغير الأبعاد في طبقة الانتقال التي تتموضع بين الكتل الكثيفة، كما يوضح الشكل 7.

طبقة عنق الزجاجة Bottleneck Layer

نحن نعلم أن كل طبقة تنتج عدد من خرائط  المزايا التي يتم تجميعهم مع خرائط المزايا للطبقات السابقة وهذا ما يجعل أبعاد الدخل بالنسبة للطبقات الأخيرة كبير جداً الذي بدوره يتطلب موارد حاسوبية ضخمة لذلك اقترح هوانغ ورفاقه استخدام طبقة عنق الزجاجة قبل كل عملية طَّي بهدف تقليل أبعاد الدخل.

بالتالي مع استخدام طبقة عنق الزجاجة تصبح العمليات المطبقة من أجل كل طبقة داخل الكتلة الكثيفة هي بالتسلسل كالتالي:

1. تقييسُ الدُّفعَةِ.
2. تابع التفعيل وحدةُ التَّصحيحِ الخطِّيِّ.
3. طَّي باستخدام مرشح ببُعد 1×1 (تمثل طبقة عنق الزجاجة).
4. تقييسُ الدُّفعَةِ.
5. تابع التفعيل وحدةُ التَّصحيحِ الخطِّيِّ.
6. طَّي باستخدام مرشح ببُعد 3×3.

دعونا الآن نوضح مفهوم طبقة عنق الزجاجة

مثال 1:

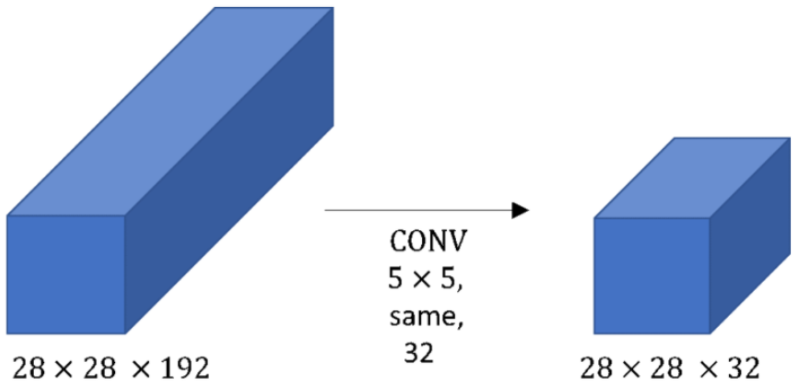
بفرض لدينا دخل ببُعد 192×28×28 حيث نطبق على الدخل 32 مرشح ببعد 5×5 وبالتالي سيكون بُعد المرشح الواحد الذي سنستخدمه 192×5×5.

حجم الخرج سيكون 32×28×28 ومن أجل حساب كل قيمة من قيم الخرج (أي من قيم 32×28×28) نحتاج إلى 192×5×5 عملية ضرب بالتالي العدد الإجمالي لعمليات الضرب التي نحتاجها لحساب كل قيم الخرج هي

5×5×192×28×28×32= 120 Million

أي نحتاج إلى 120 مليون عملية ضرب وهذه عملية مكلفة للغاية وتحتاج إلى موارد حاسوبية قوية.

مثال 2:

الآن باستخدام طبقة عنق الزجاجة نستطيع تقليل التكلفة الحسابية بنحو 10 مرات بالشكل التالي:

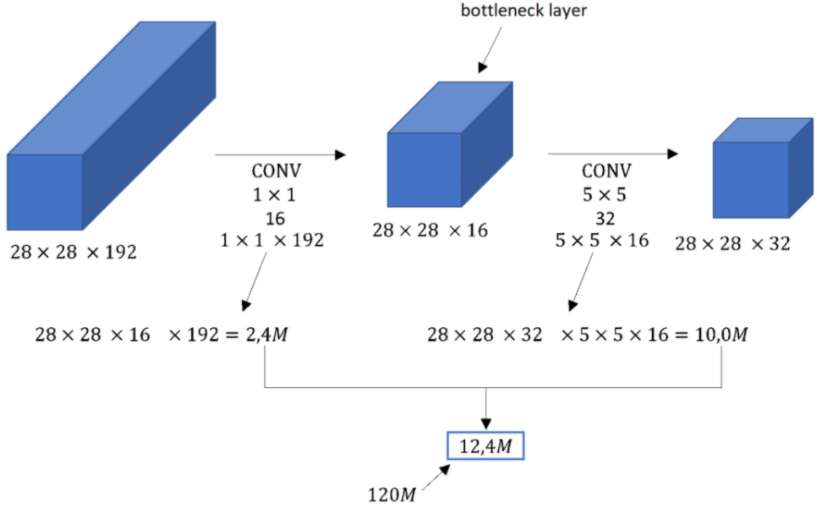
نلاحظ من الشكل 9 أنه يتم الحصول على نفس الخرج السابق (مثال 1) من أجل بُعد الدخل نفسه 192×28×28 لكن هنا العملية تمت على خطوتين.

الخطوة الأولى: 

نطبق على الدخل 16 مرشح ببُعد 28×28 وفي هذه الحالة سيكون بُعد المرشح الواحد 192×1×1 وحجم الخرج الناتج 16×28×28 وبالتالي العدد الإجمالي لعمليات الضرب سيكون:

28×28×16×1×1×192 = 2.4 Million

أي الخطوة الأولى تحتاج إلى 2.4 مليون عملية ضرب.

الخطوة الثانية:

نطبق 32 مرشح ببُعد 5×5 على خرج الخطوة الأولى وسيكون بُعد المرشح الواحد 16×5×5 والخرج الناتج هو 32×28×28 بالتالي عدد عمليات الضرب ستكون:

28×28×32×5×5×16 = 10 Million

أي الخطوة الثانية تحتاج إلى 10 مليون عملية ضرب.

 إذاً إجمالي عدد عمليات الضرب في الخطوتين الأولى والثانية هي 12.4

بالمقارنة مع المثال 1 نلاحظ أن عدد عمليات الضرب انخفض من 120 مليون إلى 12 مليون أي تقليل الكلفة الحسابية بمقدار 10 مرات.

نستنتج مما سبق أننا بإمكاننا الحصول على خرج مشابه للمثال الأول باستخدام طبقة عنق الزجاجة وبتكلفة حسابية أقل بكثير.

معماريات الشبكة الكثيفة من أجل بيانات إيمج-نت ImageNet

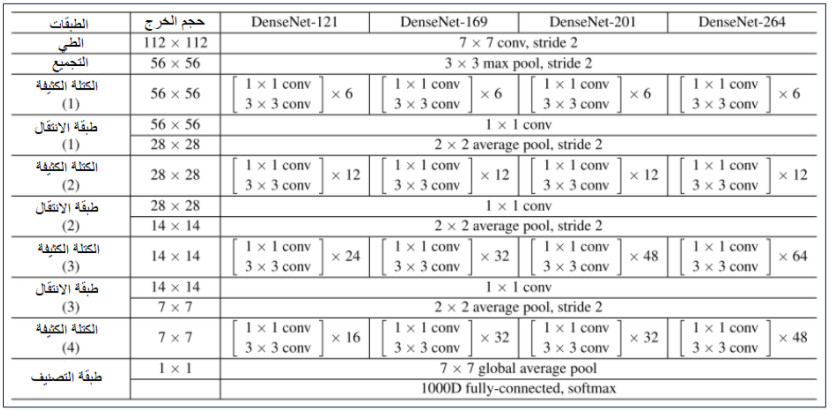
بالتدقيق في الشكل 8 نلاحظ عدة نقاط هامة:

• كل معمارية تتكون من أربع كتل كثيفة مع عدد متفاوت من الطبقات على سبيل المثال المعمارية DenseNet-121 تحتوي على 6 طبقات في الكتلة الكثيفة الأولى و 12 طبقة في الكتلة الكثيفة الثانية و24 في الكتلة الكثيفة الثالثة و 16 في الكتلة الكثيفة الرابعة، بينما تحتوي المعمارية DenseNet-169 على عدد من الطبقات [32,32,12,6] في الكتل الكثيفة الأربعة على التوالي.
• نلاحظ أن الجزء الأول من المعماريات الأربعة يتألف من طبقتين الطبقة الأولى هي طبقة طَّي يتم فيها تطبيق مرشح ببُعد 7×7 على الدخل مع خطوة تحريك مرشح الطَّي stride تساوي 2 أما الطبقة الثانية هي طبقة التجميع وتُطبق عملية التجميع وفق القيمة الكبرى Maxpooling باستخدام مرشح ببُعد 3×3 مع خطوة تحريك المرشح تساوي 2، حيث يلي هذا الجزء (الجزء الأول) الكتل الكثيفة الأربعة ثم الطبقة الأخيرة والتي هي طبقة التصنيف Classification Layer.
• نلاحظ من أجل كل طبقة داخل الكتل الكثيفة الأربعة، يتم تطبيق عملية الطَّي باستخدام مرشح 1×1 (طبقة عنق الزجاجة) تليه عملية الطَّي باستخدام مرشح 3×3.

التطبيق العملي

فيما يلي سنقوم بإجراء تصنيف للصور باستخدام نموذج للشبكة العصبونية الكثيفة مُدرب مسبقاً، حيث مجموعة البيانات المستخدمة هنا في عملية التصنيف تحتوي على ثمانية أصناف هي:

[‘dog’, ’flower’, ’motorbike’, ’person’, ’cat’, ’fruit’, ’airplane’, ‘car’]

يمكنك تحميل مجموعة البيانات من موقع كاغل من هنا.

 سنقوم أولاً بتحميل المكتبات اللازمة.

• مكتبة tensorflow هي مكتبة مفتوحة المصدر تحتوي على الأدوات اللازمة التي تتيح للمطورين بناء وتدريب نماذج تعلم الآلة بسهولة.
• مكتبة Matplotlib هي مكتبة رسومية للغة البرمجة بايثون، تحتوي هذه المكتبة على مجموعة من الأدوات تساعد على توليد الرسوم البيانية والأشكال.
• مكتبة os  تحتوي العديد من التوابع الضرورية للتفاعل مع نظام التشغيل.
• مكتبةُ بايثون العدديَّةُ numpy  تحتوي العديد من التوابع الضرورية للتعامل مع المصفوفات. 
• المكتبةُ المفتوحةُ للرُّؤيةِ الحاسُوبيَّةِ cv2 هي مكتبة مفتوحة المصدر تضم مجموعة من التوابع البرمجية التي تهدف بشكل رئيسي إلى التعامل مع تطبيقات الرؤية الحاسوبية في الزمن الحقيقي.

import tensorflow 

import numpy as np
import os
import keras
import random
import cv2
import math
import seaborn as sns

from sklearn.metrics import confusion_matrix
from sklearn.preprocessing import LabelBinarizer
from sklearn.model_selection import train_test_split

import matplotlib.pyplot as plt

from tensorflow.keras.layers import Dense,GlobalAveragePooling2D,Convolution2D,BatchNormalization
from tensorflow.keras.layers import Flatten,MaxPooling2D,Dropout

from tensorflow.keras.applications import DenseNet121
from tensorflow.keras.applications.densenet import preprocess_input

from tensorflow.keras.preprocessing import image
from tensorflow.keras.preprocessing.image import ImageDataGenerator,img_to_array

from tensorflow.keras.models import Model

from tensorflow.keras.optimizers import Adam

from tensorflow.keras.callbacks import ModelCheckpoint, ReduceLROnPlateau

import warnings
warnings.filterwarnings("ignore")

الآن سنقوم ببناء نموذج الشبكة العصبوينة الكثيفة، كما تحدثنا سابقاً أنه يوجد لدينا 8 أصناف في مجموعة البيانات ولكن نموذج الشبكة العصبونية الكثيفة (المُدرب مسبقاً) الذي سنستخدمه تم تدريبه على بيانات أيمج-نت أي مدرب على التنبؤ بـ 1000 صنف، لذلك سنقوم بحذف الطبقة الأخيرة من النموذج المدرب مسبقاً ونستبدلها بثلاث طبقات نحن نشأها تحتوي على عدد من العصبونات هي 1024 و 512 و 8 على التوالي حيث تتولى الطبقة الاخيرة (الثالثة) مهمة التصنيف وتتنبأ بـ 8 أصناف فقط.

model_d=DenseNet121(weights='imagenet',include_top=False, input_shape=(128, 128, 3)) 

x=model_d.output

x= GlobalAveragePooling2D()(x)
x= BatchNormalization()(x)
x= Dropout(0.5)(x)
x= Dense(1024,activation='relu')(x) 
x= Dense(512,activation='relu')(x) 
x= BatchNormalization()(x)
x= Dropout(0.5)(x)

preds=Dense(8,activation='softmax')(x) #FC-layer

سنقوم الآن بعرض ملخص النموذج.

model=Model(inputs=model_d.input,outputs=preds)
model.summary() 

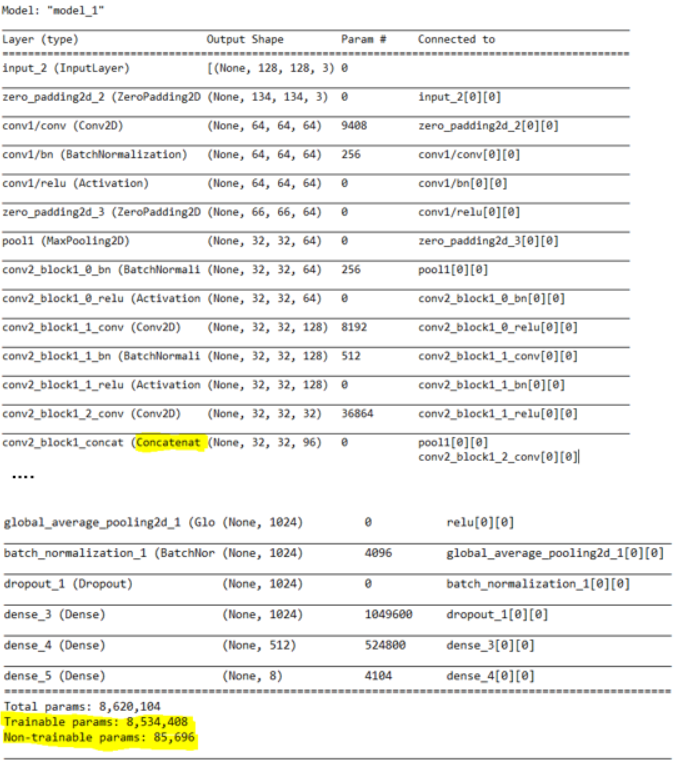
لتجنب تدريب النموذج بأكمله نقوم بتجميد طبقات النموذج الأولية وتدريب الطبقات الثمانية الأخيرة كاملة الاتصال Fully-connected، حيث كل طبقة في كيراس keras تمتلك معامل يدعى معامل قابلية التدريب Trainable يسمح لنا هذا المعامل باختيار الطبقات التي نريد تدريبها أو تجميدها.

ملاحظة: المقصود هنا بتجميد الطبقات أي الاحتفاظ بأوزان الطبقة وعدم تعديلها.

for layer in model.layers[:-8]:
    layer.trainable=False
    
for layer in model.layers[-8:]:
    layer.trainable=True  

نقوم بتحديد تابع خسارة النموذج Loss function والمُحسن Optimizer وأداة قياس آداء النموذج.

model.compile(optimizer='Adam',loss='categorical_crossentropy',metrics=['accuracy'])  

الآن نقوم بتحميل الصور مع تصنيفاتها من ملف مجموعة البيانات، أيضاً نجري معالجة أولية على الصور حيث نقوم بتحويل الصور إلى مصفوفات من أجل استخدامها في عملية التدريب.

data=[]
labels=[]
random.seed(42)
imagePaths = sorted(list(os.listdir("../input/natural-images/")))
random.shuffle(imagePaths)
print(imagePaths)

for img in imagePaths:
    path=sorted(list(os.listdir("../input/natural-images/"+img)))
    for i in path:
        image = cv2.imread("../input/natural-images/"+img+'/'+i)
        image = cv2.resize(image, (128,128))
        image = img_to_array(image)
        data.append(image)
        l = label = img
        labels.append(l)

نقوم الآن بإجراء عملية التقييسُ على البيانات وأيضاً تحويل تسميات Label الصور إلى الترميز One Hot Encoding.

data = np.array(data, dtype="float32") / 255.0
labels = np.array(labels)
mlb = LabelBinarizer()
labels = mlb.fit_transform(labels) 

تقسيم مجموعة البيانات إلى مجموعتي تدريب واختبار.

(xtrain,xtest,ytrain,ytest)=train_test_split(data,labels,test_size=0.4,random_state=42)  

التابع ReduceLROnPlateau يقوم بتقليل معدل التعلم عندما يتوقف خطأ التحقق Validation loss عن التحسن.

anne = ReduceLROnPlateau(monitor='val_accuracy', factor=0.5, patience=5, verbose=1, min_lr=1e-3)
checkpoint = ModelCheckpoint('model.h5', verbose=1, save_best_only=True)  

نقوم بتطبيق تقنية تعزيز البيانات Data Augmentation التي تتيح إنشاء إصدارات مختلفة من الصور(قلب الصورة، تدوير الصورة، قص الصورة ..)  وذلك من أجل زيادة حجم بيانات التدريب وتحسين أداء وقدرة النموذج على التعميم.

datagen = ImageDataGenerator(zoom_range = 0.2, horizontal_flip=True, shear_range=0.2)
datagen.fit(xtrain)  

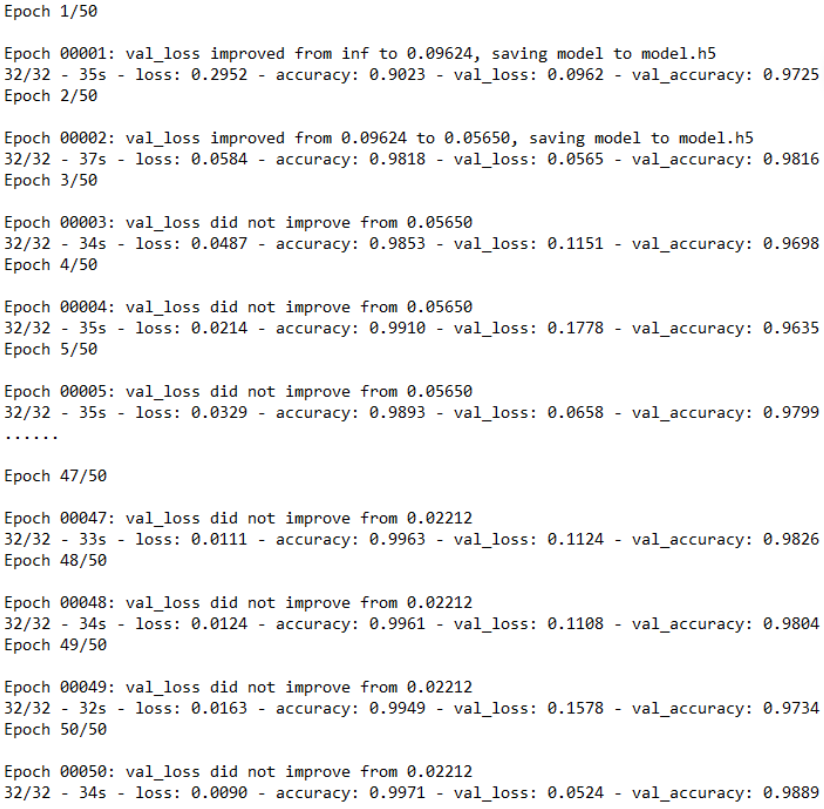
تدريب النموذج على مجموعة البيانات حيث نقوم بتحديد 50 دورة تدريب ونختار حجم الدفعة 182.

history = model.fit_generator(datagen.flow(xtrain, ytrain, batch_size=128),
               steps_per_epoch=xtrain.shape[0] //128,
               epochs=50,
               verbose=2,
               callbacks=[anne, checkpoint],
               validation_data=(xtrain, ytrain))  

حساب مقياس دقة النموذج accuracy.

ypred = model.predict(xtest)

total = 0
accurate = 0
accurateindex = []
wrongindex = []

for i in range(len(ypred)):
    if np.argmax(ypred[i]) == np.argmax(ytest[i]):
        accurate += 1
        accurateindex.append(i)
    else:
        wrongindex.append(i)
        
    total += 1
    
print('Total-test-data;', total, '\taccurately-predicted-data:', accurate, '\t wrongly-predicted-data: ', total - accurate)
print('Accuracy:', round(accurate/total*100, 3), '%')  

إجمالي عدد بيانات الاختبار Total-test-data هو 2760، حيث عدد العينات من مجموعة الاختبار التي تنبأ بها النموذج بشكل صحيح acurately-predicted-data هو 2692، وعدد العينات من مجموعة الاختبار التي أخطأ النموذج في التنبؤ بصنفها هو 68.

عرض بعض صور من مجموعة البيانات والقيم الحقيقة لها (التسمية)، وأيضاً القيمة التنبؤية للنموذج من أجل هذه الصورمن أجل أن نتمكن من إظهار بعض النتائج بشكل مرئي.  

label=['dog', 'flower', 'motorbike', 'person', 'cat', 'fruit', 'airplane', 'car']
imidx = random.sample(accurateindex, k=9)# replace with 'wrongindex'

nrows = 3
ncols = 3
fig, ax = plt.subplots(nrows,ncols,sharex=True,sharey=True,figsize=(15, 12))

n = 0
for row in range(nrows):
    for col in range(ncols):
            ax[row,col].imshow(xtest[imidx[n]])
            ax[row,col].set_title("Predicted label :{}\nTrue label :{}".format(label[np.argmax(ypred[imidx[n]])], label[np.argmax(ytest[imidx[n]])]))
            n += 1

plt.show() 

استخدام مقياس الدقة فقط من أجل قياس أداء النموذج غير كافي ومن الأفضل استخدام طرق أخرى إضافية لقياس أداء النموذج. أبرزها إيجاد مصفوفة الالتباس confusion matrix التي تمكننا من معرفة جميع الأخطاء التي ارتكبها النموذج في عملية التنبؤ.

Ypred = model.predict(xtest)

Ypred = np.argmax(Ypred, axis=1)
Ytrue = np.argmax(ytest, axis=1)

cm = confusion_matrix(Ytrue, Ypred)
plt.figure(figsize=(12, 12))
ax = sns.heatmap(cm, cmap="rocket_r", fmt=".01f",annot_kws={'size':16}, annot=True, square=True, xticklabels=label, yticklabels=label)
ax.set_ylabel('Actual', fontsize=20)
ax.set_xlabel('Predicted', fontsize=20)   

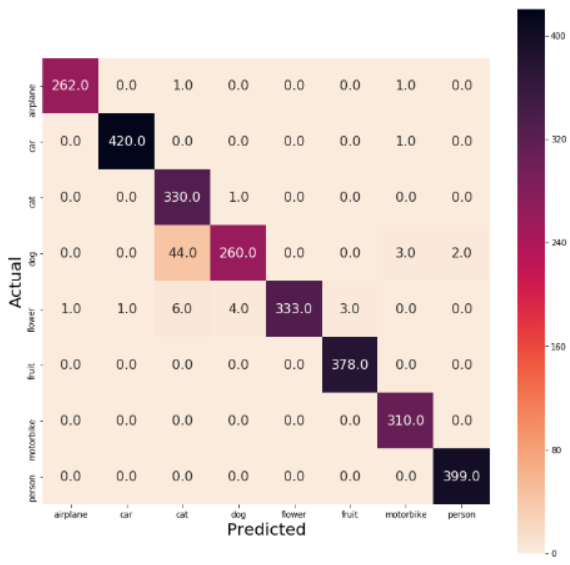
يمكنكم الاطلاع على كامل الشيفرة البرمجية في مستودع  الجت هب  الخاص بموقع الذكاء الاصطناعي باللغة العربية

الخاتمة

تعرفنا في هذا المقال على معمارية الشبكة العصبونية الكثيفة ورأينا كيف يتم تقسيم الشبكة إلى عدة كتل كثيفة بحيث يتم تحقيق الاتصال الكامل داخل كل كتلة ورأينا أيضاً كيف يتم إجراء عملية تصغير الأبعاد بين كل كتلتين بواسطة طبقة الانتقال، تعرفنا في هذا المقال على طبقة عنق الزجاجة وكيف تساهم في تخفيض أبعاد الدخل كما رأينا معماريات الشبكة الكثيفة من أجل مجموعة البيانات أيمج-نت، وأخيراً قمنا بإجراء تطبيق عملي باستخدام نموذج شبكة كثيفة مدربة مسبقاً وحصلنا على دقة 98%.

المراجــــع

1. Huang, Gao, et al. “Densely connected convolutional networks.” Proceedings of the IEEE conference on computer vision and pattern recognition. 2017
2. DenseNet Architecture Explained with PyTorch Implementation from TorchVision
3. Understanding and visualizing DenseNets
4. Densely Connected Convolutional Networks
5. Review: DenseNet — Dense Convolutional Network (Image Classification)
6. CNN Inception Network