الملاءمة الضّعيفة والمُلاءمة الزَّائدة Underfitting and Overfitting

التدّقيق العلمي: م. رامي عقّاد، م. محمّد سرميني
التدّقيق اللّغوي: هبة الله فلّاحة

مقدّمة

تُعدّ كلّ من الملاءمة الضّعيفة underfitting والمُلاءمة الزَّائدة overfitting من أكبر الأسباب التي تجعل خوارزميّات ونماذج تعلّم الآلة Machine Learning لا تحقّق نتائج جيّدة، لذا لابدّ من فهم سبب ظهورها واتّخاذ إجراءات لمنع حدوثها و لتحسين أداء النّموذج.

دعنا عزيزي القارئ نستكشف بشكل أفضل الفرق بين الملاءمة الضّعيفة والمُلاءمة الزَّائدة من خلال مثال افتراضيّ.

لنفترض أنّه يجب على طفلين إجراء اختبار في مادة الرّياضيّات، بسبب ضيق الوقت؛ تعلّم الطّفل الأوّل الجمع فقط ولم يكن قادرًا على تعلّم الطّرح أو الضّرب أو القسمة، أما الطّفل الثّاني فقد كان له ذاكرة استثنائيّة ولكنّه لم يكن جيّدًا في الرّياضيات، لذلك بدلاً من فهم الجمع والطّرح والقسمة والضّرب، قام بحفظ جميع المسائل في الكتاب مع إجاباتها، أثناء الامتحان استطاع الطّفل الأوّل حلّ مسائل الرّياضيات المتعلّقة بالجمع فقط ولم يكن قادرًا على حلّ مسائل الرياضيات التي تتضمّن العمليّات الحسابيّة الأساسيّة الثّلاث الأخرى، أمّا الطّفل الثّاني فكان قادرًا فقط على حلّ المشكلات التي حفظها من كتاب مسائل الرّياضيّات ولم يكن قادرًا على الإجابة على أيّ أسئلة أخرى. في هذه الحالة، إذا كانت أسئلة اختبار الرّياضيّات من كتابٍ مدرسيّ آخر وتضمّنت أسئلة تتعلّق بجميع أنواع العمليّات الحسابيّة الأساسيّة، فلن يتمكّن الطفلان من اجتيازها.[4]

تُظهر خوارزميّات تعلّم الآلة أحيانًا سلوكًا مشابهًا لهذين الطّفلين، أحيانًا تتعلّم فقط جزءًا صغيرًا من مجموعة بيانات التّدريب (على غرار الطّفل الذي تعلّم الإضافة فقط) في مثل هذه الحالات يُوصف أداء النّموذج بالملاءمة الضّعيفة، في حالات أخرى تقوم نماذج تعلّم الآلة بحفظ مجموعة بيانات التّدريب بالكامل (مثل الطّفل الثّاني) وتؤدّي أداءً رائعًا في الحالات المعروفة، ولكنّها تفشل في البيانات غير المرئيّة unseen dataset في مثل هذه الحالات يُوصف أداء النّموذج بالمُلاءمة الزَّائدة.

تعتبر كلاً من الملاءمة الضّعيفة والمُلاءمة الزَّائدة مفهومين أساسيّين في تعلّم الآلة، ويمكن أن يؤدّي كلاهما إلى ضعف في أداء النّموذج.

قبل التّعمق في فهم الملاءمة الضّعيفة و المُلاءمة الزَّائدة، لا بدّ من فهم بعض المصطلحات الأساسيّة التي ستساعدنا في فهم هذا الموضوع جيّدًا:

التّعميم Generalization: يُعبّر عن مدى فعاليّة تطبيق المفاهيم التي تعلّمها نموذج تعلّم الآلة على أمثلة معيّنة لم يتمّ استخدامها طوال فترة التّدريب، في التّعلّم الخاضع للإشراف Supervised learning يتمثّل الهدف الرّئيسيّ للتّعميم عند بناء نموذج تعلّم الآلة في أن يكون قادرًا على التنبّؤ بشكل دقيق بناءً على بيانات الاختبار test data وهي بيانات جديدة غير مرئيّة، أي لم يتدرّب عليها النّموذج و يكون لها نفس خصائص مجموعة التّدريب train data. 

الانحياز Bias:هو خطأ في التنبّؤ يحدث في النّموذج بسبب المبالغة في تبسيط خوارزميّات تعلّم الآلة، و هو الفرق بين القيم المتوقّعة Predicted values والقيم الفعليّة Actual values. عندما يكون لمعدّل الخطأ قيمة عالية فإنّنا نسمّيها “انحيازًا مرتفعًا High Bias” وعندما يكون لمعدّل الخطأ قيمة منخفضة، فإنّنا نسمّيها “انحيازًا منخفضًا Low Bias”.

التّباين Variance: هو الفرق بين معدّل الخطأ لبيانات التّدريب وبيانات الاختبار، إذا كان الاختلاف مرتفعًا يُطلق عليه اسم التّباين المرتفع high variance، وعندما يكون منخفضًا يُطلق عليه اسم التّباين المنخفض low variance، عادةً نحتاج إلى التّباين المنخفض لتعميم النّموذج.

الإشارة Signal: تشير إلى النّمط الأساسيّ الحقيقيّ للبيانات الذي يحتاج  نموذج تعلّم الآلة إلى استخراجه من أجل التّعلّم من البيانات و إجراء تنبّؤات دقيقة، على سبيل المثال في مجال التّعرّف على الصّور Image Recognition؛ قد تكون الإشارة هي وجود ميزات أو أشكال معيّنة في الصّورة تشير إلى كائن أو فئة معيّنة، كذلك في مجال معالجة اللّغات الطّبيعيّة Natural Language Processing (NLP)، قد تكون الإشارة هي المعنى الدّلاليّ لبعض الكلمات أو العبارات التي تساعد النّموذج على فهم سياق الجملة.

تعدّ قدرة نموذج التّعلّم الآليّ على التقاط الإشارة الأساسيّة في البيانات واستخدامها بدقّة أمرًا بالغ الأهمية؛ فالنّماذج الأكثر قدرة على استخراج واستخدام الإشارة في البيانات تكون أكثر دقّة وفعاليّة في التنبّؤ عن غيرها من النّماذج.

الضّوضاء Noise: هي البيانات غير الضّرورية وغير ذات الصّلة والتي يمكن أن تحجب الإشارة الأساسية في البيانات أو تتداخل معها مما يُقلّل من أداء النّموذج، فمثلًا يمكن أن تتسبّب الضّوضاء في حجب الإشارة الأساسيّة في البيانات أو التّداخل معها، و لتقليل تأثير الضّوضاء على نماذج التّعلّم الآليّ، يمكن استخدام تقنيّات معالجة البيانات Data Preprocessing  لإزالة أو تقليل تأثير الضّوضاء على البيانات، مما يسهّل على النّموذج التّعلّم وإجراء تنبّؤات دقيقة. 

ما المقصود بالملاءمة الضّعيفة Underfitting؟

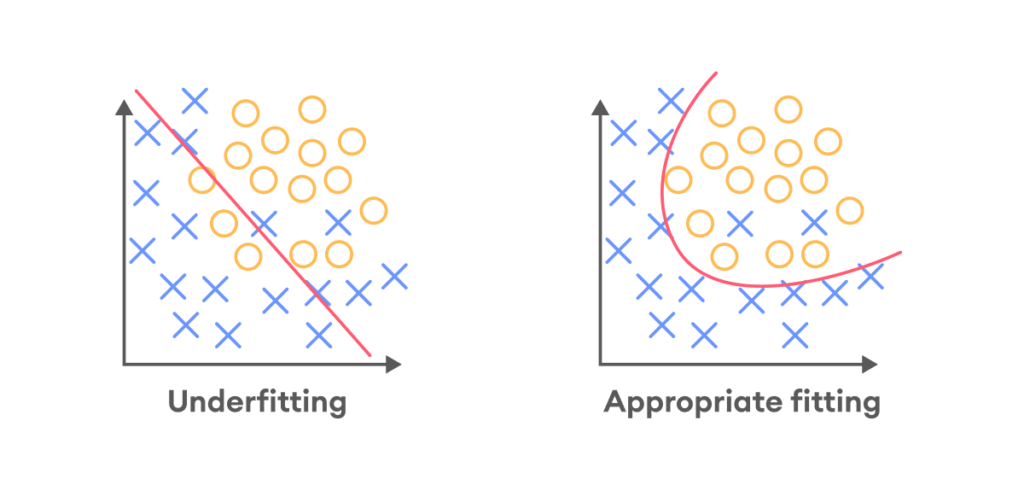
تحدث عندما يكون للنّموذج انحياز كبير جدًّا و يكون النّموذج غير قادر على التقاط الأنماط المعقّدة في البيانات كما هو موضّح في الشّكل (1)، يؤدّي هذا إلى ارتفاع أخطاء التّدريب والتّحقّق training/validation errors؛ لأنّ النّموذج ليس معقّدًا بدرجة كافية لتصنيف البيانات.

تميل نماذج تعلّم الآلة ذات الملاءمة الضّعيفة إلى ضعف الأداء في كلٍّ من مجموعات التّدريب والاختبار (مثل الطّفل الذي تعلّم الجمع فقط ولم يكن قادرًا على حلّ المشكلات المتعلّقة بالعمليّات الحسابيّة الأساسيّة الأخرى أثناء امتحان الرّياضيّات).

عادة ما يكون للنّموذج ذي الملاءمة الضّعيفة تحيّزًا مرتفعًا high bias وتباينًا منخفضًا low variance.

كيفيّة الكشف عن الملاءمة الضّعيفة

بعد أن تعرّفنا على مفهوم الملاءمة الضّعيفة سنتطرّق إلى طرق الكشف عنها:

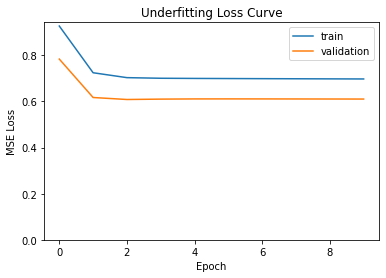
1. خسارة التّدريب و الاختبار: إذا كانت ملاءمة النّموذج ضعيفة، فستكون الخسارة loss لكلٍّ من بيانات التّدريب و التّحقّق عالية إلى حدٍّ كبير، كما هو موضّح في الشّكل (2) ،حيث نلاحظ أنّ الخسارة عالية لكلّ من التّدريب والاختبار.

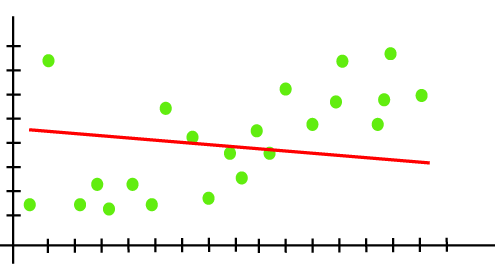
2. الرّسم البيانيّ للتنبّؤ مبالغ في بساطته: إذا تمّ عمل رسم بيانيّ لنقاط البيانات وكان منحنى المصنّف مفرط في التّبسيط، فعلى الأرجح يكون النّموذج ضعيف الملاءمة، كما هو موضّح في الشكل (3). في هذه الحالات يجب تجربة نموذج أكثر تعقيدًا.

أسباب حدوث الملاءمة الضّعيفة

1. الانحياز العالي والتّباين المنخفض.
2. حجم مجموعة بيانات التّدريب المستخدمة غير كاف.
3. النّموذج بسيط للغاية.
4. بيانات التّدريب ليست نظيفة وتحتوي أيضًا على ضوضاء.

طرق تجنّب الملاءمة الضّعيفة

هناك العديد من الأشياء التي يمكنك القيام بها لمنع الملاءمة الضّعيفة في نماذج تعلّم الآلة:

1.  تدريب نموذج أكثر تعقيدًا: يعدّ الافتقار إلى تعقيد النّموذج ليناسب خصائص البيانات هو السّبب الرّئيسيّ وراء ضعف ملاءمة النّموذج. على سبيل المثال، قد يكون لديك بيانات لها ما يزيد عن 100000 صفّ rows وأكثر من 30 مُعامل، إذا قمت بتدريب البيانات باستخدام نموذج الغابة العشوائيّة Random Forest وقمت بإسناد قيمة صغيرة  (على سبيل المثال 2)  لمُعامل “أقصى عمق max depth” الذي يعبّر عن عدد الانقسامات التي يُسمح لكلّ شجرة قرار Decision tree إجراؤها، فسيكون نموذجك بالتّأكيد ذا ملاءمة ضعيفة وسيساعدنا تدريب نموذج أكثر تعقيدًا على حلّ مشكلة ضعف الملاءمة، في المثال السابق مثلاً، نقوم بتدريب نموذج ذي قيمة أعلى لمُعامل أقصى عمق. 
2. زيادة وقت التّدريب: قد يتسبّب الإنهاء المبكّر لعمليّة التّدريب إلى ضعف الملاءمة، يمكن حلّ ذلك عن طريق زيادة عدد دورات التّدريب epochs للحصول على نتائج أفضل.
3. إزالة الضّوضاء من البيانات:  سبب آخر لضعف الملاءمة هو وجود القيم المتطرّفة والقيم غير الصّحيحة في مجموعة البيانات، يمكن أن تساعد تقنيّات تنظيف البيانات Data cleaning في التّعامل مع هذه المشكلة.
4. ضبط معاملات التّنظيم: يمكن أن يتسبّب معامل التّنظيم regularization coefficient في كلّ من الملاءمة الضّعيفة والملاءمة الزّائدة.
5. تجربة نموذج مختلف: إذا لم تنجح أيًّا من الحلول المذكورة أعلاه، يمكنك تجربة نموذج مختلف (عادةً يجب أن يكون النّموذج الجديد أكثر تعقيدًا بطبيعته). على سبيل المثال يمكنك محاولة استبدال النّموذج الخطّيّ بنموذج متعدّد الحدود ذي تّرتيب أعلى higher-order polynomial model.

ما المقصود بالمُلاءمة الزَّائدة Overfitting؟

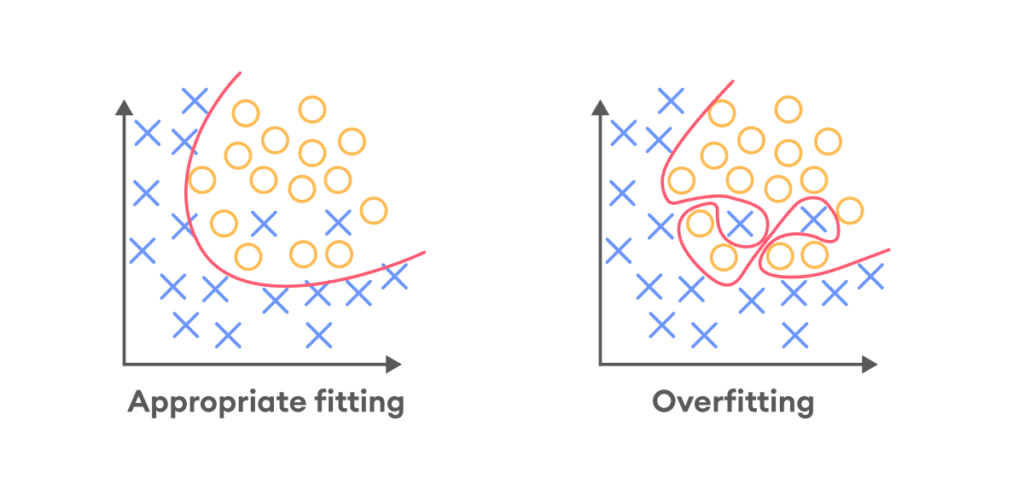
يُوصف النّموذج بأنه ذو مُلاءمة زّائدة عندما يعمل بشكل جيّد على بيانات التّدريب، ولكنّه يفشل في الأداء بنفس المستوى على بيانات التّحقّق (مثل الطّفل الذي حفظ كلّ مسائل كتاب الرّياضيّات، وواجه صعوبة عند محاولة حلّ مسائل من أيّ كتاب غير كتابه). يفشل نموذج المُلاءمة الزَّائدة في التّعميم بشكل جيّد، كما هو موضّح في الشّكل (4) حيث يتعرّف على الضّوضاء وأنماط بيانات التّدريب، لدرجة أنّه يؤثّر سلبًا على أداء النّموذج على البيانات الجديدة.

كيفيّة الكشف عن المُلاءمة الزَّائدة

بعد أن تعرّفنا على مفهوم المُلاءمة الزَّائدة سنتطرّق إلى طرق الكشف عنها:

1. استخدم تقنيّة التّحقّق المتقاطع cross validation لتقدير دقّة النّموذج: أكثر تقنيّات إعادة التّشكيل* resampling technique شيوعًا هي ك-أجزاء التحقق المتقاطع k-fold cross-validation؛ التي تسمح بتدريب النّموذج واختباره على مجموعات فرعيّة مختلفة من بيانات التّدريب، وبناء تقدير لأداء نموذج تعلّم الآلة على البيانات غير المرئيّة (بيانات الاختبار)، عيبها أنّها تستغرق وقتًا طويلًا ولا يمكن تطبيقها على النّماذج المعقّدة، مثل الشّبكات العصبونيّة العميقة DNN. يُذكَر أن تقنيّات إعادة التّشكيل resampling هي تقنيات تُستخدم في تعلّم الآلة والإحصاء لتقييم أداء النّموذج؛ من خلال إنشاء مجموعات بيانات تدريب واختبار جديدة من مجموعة بيانات موجودة. تُستخدم تقنيات إعادة التشّكيل لتحسين دقّة وتعميم النموذج.
2. استخدام مجموعة بيانات التّحقّق validation data: بمجرّد تدريب النّموذج على مجموعة التّدريب، يمكنك تقييمه على مجموعة بيانات التّحقّق، ثمّ مقارنة دقّة النّموذج في مجموعة بيانات التّدريب ومجموعة بيانات التّحقّق، يسمح التّباين الكبير في هاتين النّتيجتين بافتراض أنّ لديك نموذجًا يوصف بالملاءمة الزّائدة.[4]
3. هناك طريقة أخرى لاكتشاف الملاءمة الزّائدة وهي البدء بنموذج مبسّط يعمل كمعيار. باستخدام هذا النّهج، لو بدأت بنموذج بسيط ثمّ قمت بتدريب نموذج أكثر تعقيدًا حينها سيتّضح إن كان التّعقيد يُحسّن من أداء النّموذج أم لا، يُعرف هذا المبدأ باسم اختبار شفرة أوكام Occam’s razor test. يشير هذا المبدأ إلى أنّه مع تساوي كلّ شيء، فإنّ الحلول الأبسط للمشكلات مفضّلة على الحلول الأكثر تعقيدًا (إذا لم يتحسّن نموذجك بشكل ملحوظ بعد استخدام نموذج أكثر تعقيدًا، فمن الأفضل استخدام نموذج أبسط).[4]

أسباب حدوث المُلاءمة الزَّائدة

1. تباين كبير وانحياز منخفض.
2. النّموذج معقّد للغاية.
3. حجم بيانات التّدريب قليل.

طرق تجنّب المُلاءمة الزَّائدة

هناك العديد من الأشياء التي يمكنك القيام بها لمنع المُلاءمة الزَّائدة في نماذج تعلّم الآلة:

•  زيادة البيانات: في معظم الأحيان يمكن أن تساعد إضافة المزيد من البيانات نماذج تعلّم الآلة في اكتشاف النّمط الحقيقيّ للنّموذج، والتّعميم بشكل أفضل ومنع الملاءمة الزّائدة للنّموذج، ومع ذلك ليس هذا هو الحال دائمًا لأنّ إضافة المزيد من البيانات غير الدّقيقة أو التي تحتوي على العديد من القيم المفقودة missing value يمكن أن يؤدّي إلى نتائج أسوأ.
• التّوقّف المبكّر Early stopping: في الخوارزميّات التّكراريّة iterative algorithms، من الممكن قياس أداء تكرار النّموذج  حتى عدد معيّن من التّكرارات، وتعمل التّكرارات الجديدة على تحسين النّموذج، عند نقطة معيّنة يمكن أن تتدهور قدرة النّموذج على التّعميم عندما يبدأ في الإفراط في استيعاب بيانات التّدريب، يشير التّوقّف المبكّر إلى إيقاف عمليّة التّدريب قبل أن يجتاز النّموذج تلك النّقطة.
•  تعزيز البيانات Data Augmentation: في تعلّم الآلة تزيد تقنيّات تعزيز البيانات من كميّة البيانات عن طريق تغيير البيانات الموجودة مسبقًا بشكل طفيف وإضافة نقاط بيانات جديدة، أو عن طريق إنتاج بيانات تركيبيّة من مجموعة بيانات موجودة مسبقًا. فمثلاً في مجال الرّؤية الحاسوبيّة Computer vision، يتمّ استخدام التّحويلات الهندسيّة Geometric transformations، المسح العشوائيّ Random erasing، خلط الصّور Mixing images و العديد من التّقنيات الأخرى. أمّا في معالجة اللّغات الطبيعيّة، من أهمّ الأساليب المستخدمة في تعزيز البيانات: التّلاعب في بناء الجملة Syntax-tree manipulation و إدخال عشوائيّ للكلمات Random word insertion و غيرها.
• إزالة المزايا Remove features: يمكنك إزالة المزايا غير ذات الصّلة من البيانات للتّحسين من أداء النّموذج، قد لا تساهم العديد من المزايا في مجموعة البيانات كثيرًا في التنبّؤ، يمكن أن تؤدّي إزالة المزايا غير الأساسيّة إلى تعزيز الدّقّة وتقليل الملاءمة الزّائدة.
• التّنظيم  Regularization L1، L2: عبارة عن عمليّة إضافة عوامل إضافيّة إلى نموذج التّعلّم للتّحسين في الأداء عندما يتعامل النّموذج مع بيانات جديدة غير معروفة، و يُعدّ التّنظيم مصطلحًا إضافيًّا يضاف إلى تابع الخسارة loss function  لفرض قيود على أوزان مُعاملات الشّبكة الكبيرة لتقليل الملاءمة الزّائدة، تنظيم L1 و L2 هما الطّريقتان المستخدمتان على نطاق واسع، على الرّغم من أنّهما تقيدان الأوزان الكبيرة إلّا أنّ كلاهما يحقّق التّنظيم بشكل مختلف.[1]

تنظيم L1: يضيف تنظيم L1 نسخة مصغّرة من معيار L1 لمعاملات الوزن إلى تابع الخسارة. معادلة التّنظيم  L1 هي:

حيث يمثّل Lreg الخسارة المنتظمة، و يمثّل E(W) قيمة الخطأ التي تقيس مدى ملاءمة النّموذج لبيانات التّدريب، بينما λ هو المعامل الأساسيّ hyperparameter وأخيرًا 1||W|| هو معيار L1 للأوزان.

لو كانت قيمة الخطأ E(w) صفرًا، بينما قيمة الأوزان ليست صفريّة، هذا يعني أنّ قيمة الخسارة المنتظمة Lreg ستكون عالية، لكنّ الهدف الأساسيّ للتٌحسين Optimization هو التّقليل من قيمة Lreg، فلو قمنا بتعيين قيمة صفر للأوزان ستقلّ قيمة الخسارة Lreg و يزداد التّباين.

تنظيم L2: هو إضافة تربيع معيار L2 للأوزان إلى تابع الخسارة loss function. معادلة التّنظيم L2 هي كما يلي:

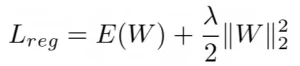
حيث يمثّل Lreg الخسارة المنتظمة، ويمثّل E (W) قيمة الخطأ التي تقيس مدى ملاءمة النّموذج لبيانات التّدريب، بينما λ هو المعامل الأساسيّ و يعرف باسم معدل التّنظيم، وأخيرًا ||W|| هو معيار L2 للأوزان.

إنّ اشتقاق هذه المعادلة هو عبارة عن معادلة تحديث الوزن أثناء عمليّة التّحسين optimization:

η هو معدّل التّعلّم

نرى أنّ الأوزان القديمة يتمّ تحجيمها بمقدار (1-ηλ) أو تتلاشى مع كلّ تحديث للتّدرّج، وبالتّالي يؤدّي تنظيم L2 إلى أوزان أصغر.

•  التّجميع Ensembling: تقوم طرق التّجميع بدمج التنبّؤات من العديد من النّماذج المختلفة، لا تستخدم طرق التّجميع مع الملاءمة الزّائدة فقط، بل تساعد أيضًا في حلّ مشكلات تعلّم الآلة المعقّدة (مثل الجمع بين الصّور المأخوذة من زوايا مختلفة)، أكثر طرق التّجميع شيوعًا هي التّعزيز و التّجميع.
• • التّعزيز Boosting: تقوم بتدريب عدد كبير من النّماذج الضّعيفة بالتّسلسل، ويتعلّم كلّ تسلسل من أخطاء النموذج السّابق له في السّلسلة، حيث يتمّ الجمع بين تنبّؤات جميع النّماذج الضّعيفة لإنشاء نموذج قويّ يتمتع بدقّة أفضل من دقّة أي نموذج وحده.
  • التّجميع Bagging هو أسلوب آخر لتقليل الملاءمة الزّائدة، حيث يتمّ تدريب عدد كبير من النّماذج القويّة، ثمّ يتمّ دمج تنبّؤات جميع النّماذج لعمل التنبّؤ النّهائيّ، عن طريق إيجاد متوسّط التّوقّعات أو باستخدام تصويت الأغلبيّة (في التّصنيف).

• تعطيل عمل العُصبُونات Dropout: الفكرة الرّئيسيّة لهذه التّقنية هي إسقاط الوحدات units بشكل عشوائيّ من الشّبكات العصبونيّة أثناء التّدريب، تمّ مناقشتها في الورقة التّالية:Dropout: A Simple Way to Prevent Neural Networks from Overfitting (2014) تعطيل عمل العصبونات: طريقة بسيطة لمنع الشّبكة العصبونية من الملاءمة الزّائدة (2014)  بواسطة سريفاستافا Srivastava  وآخرين. أثناء التّدريب تشكّل عيّنات تعطيل عمل العُصبُونات عددًا كبيرًا من الشّبكات “الضّعيفة” المختلفة، يتمّ تحقيق تعطيل عمل العُصبُونات من خلال إنشاء مصفوفة بالرّسم من توزيع برنوليّ Bernoulli  باحتمال p (للحصول على 1) [أي احتمال تعطيل عمل العُصبُونات هو1-p] ثمّ القيام بعملية ضرب على مستوى العنصر element-wise multiplication بين  هذه المصفوفة  و مخرجات الطّبقات المخفيّة، يوضّح الشّكل (5) تعطيل عمل العُصبُونات أثناء مرحلة التّدريب، حيث يمثل الشكل (a) نموذجًا لشبكة عصبونيّة ذات طبقتين خفيّتين، أمّا الشّكل (b) فهو يمثّل شبكة ضعيفة تمّ إنتاجها عن طريق تطبيق تقنيّة تعطيل عمل العصبونات على الشّبكة الموجودة على اليسار (الشكل a)، الوحدات التي بداخلها علامة X تمثّل الوحدات التي تمّ تعطيلها.[1]

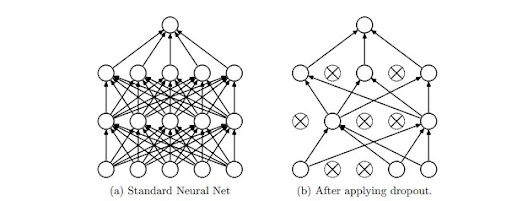
يضمن تعطيل عمل العُصبُونات عدم اعتماد أيّ خلية عصبونيّة أكثر من اللّازم على الخلايا العصبونيّة الأخرى، وتعلّم شيئ مفيد بدلًا من ذلك. يمكن تطبيق تعطيل عمل العُصبُونات بعد طبقات الطّيّ أو التّجميع أو الطَّبَقة ذات الاتصال الكامل Fully connected layer .

التّطبيق العمليّ

بالنسبة لبيانات التّدريب سنستخدم مجموعة بيانات تيتانيك Titanic، والتي يمكن تنزيلها عبر رابط  مستودع غيت هب.

1. أوّلًا نقوم باستيراد المكتبات و الحزم والتّوابع اللّازمة، والتي من أهمّها مكتبة تحليل البيانات في بايثون (بانداس) Pandas، مكتبة بايثون العدديّة numpy، مكتبة الرَّسم الرِّياضيّ في بايثون (ماتبلوت) matplot ومكتبة اس-كي للتّعلّم sklearn. كما هو موضّح في الشّيفرة البرمجيّة التّالية:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import cross_val_score, learning_curve, validation_curve

2. لقراءة البيانات الخاصّة بالتّدريب train data و بيانات الاختبار test data نقوم باستخدام التّابع read_csv من مكتبة بانداس، ثمّ نقوم بدمجهما في مجموعة بيانات واحدة باستخدام التّابع append. لطباعة أوّل خمسة أسطر من البيانات نستخدم التّابع head()، ويكون الخرج كما هو في الشكل (6).

df_train = pd.read_csv('/content/train.csv')
df_test = pd.read_csv('/content/test.csv')
df_comb = df_train.append(df_test)


X = pd.DataFrame()
df_comb.head()

الخرج النّاتج من تنفيذ الشّيفرة البرمجيّة df_comb.head()، حيث نلاحظ أنّ البيانات لديها اثنا عشر عمودًا وهي كالآتي 

1. PassengerId: وهو عبارة عن رقم تعريفيٌ خاص بكلّ راكب.
2. Survived: يعبّر عن النّجاة، لو كانت القيمة 1 فهذا يعني أنّ الرّاكب نجا من الموت، والقيمة 0 تعبّر عن موت الرّاكب.
3. PClass: يعبٌر عن فئة التّذكرة، ولها ثلاثة قيم محتملة (1 ، 2 ، 3).
4. Name: وهو عبارة عن اسم الرّاكب.
5. Sex: يعبّر عن جنس الرّاكب.
6. Age: يعبّر عن عمر الرّاكب.
7. SibSp: تمثّل عدد الأشقاء / الأزواج على متن السّفينة.
8. Parch: يمثّل عدد الآباء / الأبناء على متن السّفينة.
9. Ticket: يمثّل رقم التّذكرة التي يحملها الرّاكب.
10. Fare: يمثّل الأجرة التي دفعها كلّ مسافر مقابل تذكرته.
11. Cabin: يمثّل رقم المقصورة الخاصّة بالرّاكب.
12. Embarked: تمثّل ميناء المغادرة، ولها ثلاثة قيم محتملة (C, Q ,S).

3. نقوم بانشاء بعض التّوابع لتشفير البيانات الموجودة في المجموعة إلى صيغ رقميّة ليتمكّن نموذج تعلّم الآلة من التّعامل معها، في هذه الحالة يقوم التّابع encode_sex بتحويل الجنس sex إلى 1 إذا كان الجنس أنثى و 0 إذا كان ذكرًا، كما ويقوم التّابع family_size بتشفير أحجام الأُسر بحيث يمكن أن تكون 1 أو 2 أو 3 أو 4، يتمّ التّعامل مع جميع العائلات الأكبر من 3 على أنّها 4؛ هذا يقلّل من الانتشار في متغيّر FamilySize حيث أنّه يتمّ تقليل نطاق القيم للمتغيّر(من 1 إلى 4)، فيصبح تحليل البيانات أسهل لأنّ المتغيّر لم يعد يميل نحو العائلات الأكبر وبالتّالي يزيد من أهمّية المتغير.

def encode_sex(x):
    return 1 if x == 'female' else 0


def family_size(x):
    size = x.SibSp + x.Parch 
    return 4 if size > 3 else size


X['Sex'] = df_comb.Sex.map(encode_sex)
X['Pclass'] = df_comb.Pclass
X['FamilySize'] = df_comb.apply(family_size, axis=1)

4. نقوم بحساب متوسّط الأجرة التي دفعها الرّكاب fare_median ومتوسّط العمرage_mean لكلّ مجموعة من الجنس والفئة Pclass باستخدام التّابعgroupby.

fare_median = df_train.groupby(['Sex', 'Pclass']).Fare.median()
fare_median.name = 'FareMedian'


age_mean = df_train.groupby(['Sex', 'Pclass']).Age.mean()
age_mean.name = 'AgeMean'

5. نقوم بانشاء التّابع join الذي يستقبل المدخلين: إطار بيانات df و سلسلة البيانات stat التي سيتمّ دمجها مع إطار البيانات، حيث يتم الدّمج باستخدام التّابع merge، يحدّد المعامل left_on الأعمدة المراد دمجها في df، وهما Sex و Pclass و يحدّد المعامل right_index أنّه يجب استخدام فهرس stat للدّمج. أخيرًا تحدّد المعلّمة how أنّ الصلة يجب أن تكون صلة يسرى.

def join(df, stat):
    return pd.merge(df, stat.to_frame(), left_on=['Sex', 'Pclass'], right_index=True, how='left')

6. يتمّ استبدال القيم المفقودة في العمودين الأجرة و أعمار الرّكاب باستخدام fare_median و age_mean، ويتمّ تخزينهم النّاتج في إطار البيانات X.

يقوم التّابع head بطباعة أوّل خمسة أسطر في إطار البيانات X، لاحظ أنّه تمّ إضافة العمودين Fare , Age كما هو موضّح في الشكل (7) أدناه.

X['Fare'] = df_comb.Fare.fillna(join(df_comb, fare_median).FareMedian)
X['Age'] = df_comb.Age.fillna(join(df_comb, age_mean).AgeMean)
X.head()

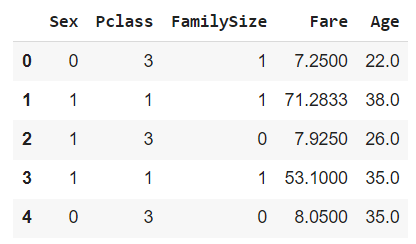
7. المتغيّران الأجرة  و العمر في X هي متغيّرات كميّة مستمرّة Continuous Quantitative Variable، هذا يعني أنّها يمكن أن تأخذ أيّ قيمة رقميّة ضمن نطاق معيّن؛ لذا قمنا بإنشاء التّابعين quantiles و discretize  لتقدير البيانات (تحويلها الى متغيّرات كمية منفصلة Quantitative Variable Discrete) ،أي تقوم بتجميع القيم في فئات منفصلة، من أجل تبسيط التّحليل.

يستقبل التابع  quantiles مُدخلين هما: series سلسة من البيانات وnum عدد صحيح يشير إلى عدد الكميّات quantiles المطلوب تقسيم السّلسلة إليها، ثمّ يحسب عدد الكميّات من السّلسلة ويعيد مصفوفة تحتوي على حدود الكميّات النّاتجة. حيث يستخدم التّابع qcut من مكتبة بانداس لحساب الكميّات ويتمّ تعيين retbins = True لإرجاع حدود الكمّيات. ثمّ يقوم التّابع discretize باستقبال سلسلة البيانات ومجموعة من الحدود bins كمدخلات، و يفرز القيم الموجودة في السّلسلة، و يتمّ ذلك باستخدام التّابع cut من مكتبة بانداس، الهدف منها فصل مجموعات الرّكاب حسب الأجرة التي دفعوها وأعمارهم.

يقوم التّابع head بطباعة أوّل خمسة أسطر في إطار البيانات X، لاحظ في الشّكل (8) أدناه أنّ قيم البيانات في العمودين Fare , Age تغيّرت بعد تطبيق التّابع discretize عليها

def quantiles(series, num):
    return pd.qcut(series, num, retbins=True)[1]


def discretize(series, bins):
    return pd.cut(series, bins, labels=range(len(bins)-1), include_lowest=True)
    
X['Fare'] = discretize(X.Fare, quantiles(df_comb.Fare, 10))
X['Age'] = discretize(X.Age, quantiles(df_comb.Age, 10))
X.head()

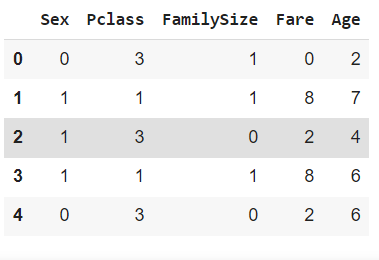
8. نقوم بتقسيم البيانات إلى مجموعات تدريب واختبار X_train, X_test, y_train. 

تعتبر X_train مجموعة فرعيّة من X، حيث تحتوي على صفوف إطار البيانات X من بدايتها حتى الفهرس index المقابل لعدد الصفوف في إطار البيانات df_train.

X_test هي مجموعة فرعيّة أخرى من X، تحتوي على الصّفوف المتبقيٌة في إطار البيانات X، بدءًا من الفهرس المقابل لعدد الصّفوف في df_train وتستمرّ حتّى آخر صفّ في X.

X_train = X.iloc[:df_train.shape[0]]
X_test = X.iloc[df_train.shape[0]:]
y_train = df_train.Survived

9. إعداد نموذج الغابة العشوائيّة Random Forest باستخدام المُصنّف  RandomForestClassifier الذي يأخذ المُعاملات التالية:  n_estimators لتحديد عدد الأشجار التي سيتمّ استخدامها في النّموذج (تمّ تعيينها للقيمة 100)، المعامل bootstrap والذي يحدّد فيما إذا كان سيتمّ استخدام مجموعة البيانات بأكملها لبناء كلّ شجرة؟ في هذه الحالة تكون قيمتها False أمّا في حالة استخدام جزء من البيانات فيتمّ تعيين القيمة True.

ثمّ يتمّ تدريب النّموذج  clf_1 على بيانات التّدريب باستخدام التّابع fit، من أجل عمليّة التّحقّق المتقاطع cross validation، تمّ تحديد  7 أجزاء folds.

clf_1 = RandomForestClassifier(n_estimators=100, bootstrap=True, random_state=0)
clf_1.fit(X_train, y_train)
# Number of folds for cross validation
num_folds = 7

10. من أجل رسم نتائج التّدريب والاختبار نقوم ببناء التّابع plot_curve الذي سيقوم بحساب المتوسّط و الانحراف المعياريّ لكلّ منها لاستخدامها في الرّسم. 

def plot_curve(ticks, train_scores, test_scores):
    train_scores_mean = -1 * np.mean(train_scores, axis=1)
    train_scores_std = -1 * np.std(train_scores, axis=1)
    test_scores_mean = -1 * np.mean(test_scores, axis=1)
    test_scores_std = -1 * np.std(test_scores, axis=1)


    plt.figure()
    plt.fill_between(ticks, 
                     train_scores_mean - train_scores_std, 
                     train_scores_mean + train_scores_std, alpha=0.1, color="b")
    plt.fill_between(ticks, 
                     test_scores_mean - test_scores_std, 
                     test_scores_mean + test_scores_std, alpha=0.1, color="r")
    plt.plot(ticks, train_scores_mean, 'b-', label='Training score')
    plt.plot(ticks, test_scores_mean, 'r-', label='Test score')
    plt.legend(fancybox=True, facecolor='w')


    return plt.gca()

11. بناء التّابع plot_validation_curve الذي يقوم برسم منحنى التّحقّق، clf تمثّل المصنّف المستخدم، X,y تمثّلان بيانات التّدريب، يمكن تحديد معامل و تحديد نطاق قيمته باستخدام param_name و param_range على التّوالي، ويستخدمان لضبط قيمة أحد المعاملات الأساسيّة Hyper parameters للنّموذج.

def plot_validation_curve(clf, X, y, param_name, param_range, scoring='roc_auc'):
    plt.xkcd()
    ax = plot_curve(param_range, *validation_curve(clf, X, y, cv=num_folds, scoring=scoring, param_name=param_name, 
    param_range=param_range, n_jobs=-1))
    ax.set_title('')
    ax.set_xticklabels([])
    ax.set_yticklabels([])
    ax.set_xlim(2,12)
    ax.set_ylim(-0.97, -0.83)
    ax.set_ylabel('Error')
    ax.set_xlabel('Model complexity')
    ax.text(9, -0.94, 'Overfitting', fontsize=22)
    ax.text(3, -0.94, 'Underfitting', fontsize=22)
    ax.axvline(7, ls='--')
    plt.tight_layout()

12. وأخيرًا نقوم باستدعاء التّابع plot_validation_curve وتمرير البيانات اللّازمة له، لاحظ تمّ تعيين النّطاق لأقصى عمق max_depth بين القيمتين 2 و 13.

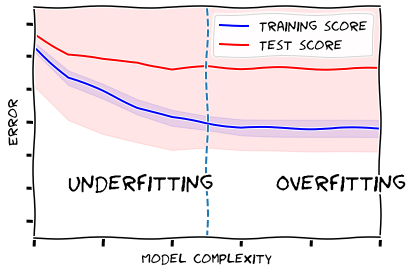
يوضّح الخرج النّاتج في الشّكل (9) منحنى التّدريب (باللّون الأزرق) ومنحنى الاختبار (باللّون الأحمر)،لاحظ أنّه في البداية كان النّموذج في حالة الملاءمة الضّعيفة، لأنّ قيمة الخسارة عالية لكلا المنحنيان، ولكن في النّهاية أصبح المنحنيان بعيدين عن بعضهما؛ و هذا يعني أنّ النّموذج في حالة الملاءمة الزّائدة؛ أي أنّ التّعقيد الزّائد للنموذج لم يكن مُجديًا، و كما يتضح من الرّسم فإنّ أفضل قيمة لأقصى عمق max_depth هي 7.

plot_validation_curve(clf_1, X_train, y_train, param_name='max_depth', param_range=range(2,13))

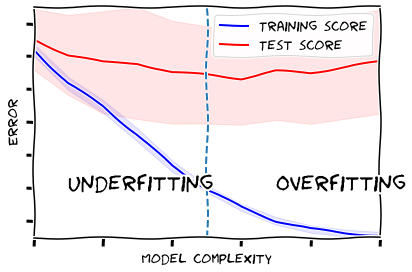
لحلّ مشكلة التعقيد الزّائد في النّموذج و لتجنّب الملاءمة الزّائدة يمكن تجربة أكثر من حل:

1. تقليل تعقيد النموذج: في التابع plot_validation_curve ، تمّ تعيين param_range إلى النطاق (2 ، 13)، مما يعني أنّ الحدّ الأقصى لعمق أشجار القرار Decision trees في الغابة العشوائيّة مسموح له أن يتراوح من 2 إلى 12. لتقليل تعقيد النموذج يمكن تقليل أقصى عمق للأشجار إلى نطاق أصغر من القيم.
2. زيادة التنظيم: كما ذكرنا سابقًا فإنّ التنظيم يلعب دورًا مهمًّا في تقليل الملاءمة، لذا سنقوم بزيادة التّنظيم في نموذج الغابة العشوائيّة. عن طريق ضبط المعاملين min_samples_split و min_samples_leaf لقيم أعلى للتأكد من أنّ كلّ عقدة طرفيّة بها أقلّ عدد من العينات.
3. استخدام التّحقق المتقاطع: تمّ تعيين متغير num_folds على 7، يمكن تعيينه لقيمة أكبر لتجنب حدوث الملاءمة الزّائدة.
4. تجربة مصنّف أخر مثل مصنّف شجرة القرار DecisionTreeClassifier و مصنّف Naive Bayes وغيرها من المصنّفات.

13. قمنا بتعديل قيمة المعامل n_estimators إلى 50، وزيادة عدد الأجزاء num_folds إلى 10 كما هو موضّح في الشيفرة البرمجيّة التالية.

لاحظ الفرق بين الخرج في الشّكل (9) والشّكل (10)، من الواضح أنّ تقليل تعقيد النموذج أدّى الى تقليل البعد بين المنحنيين، وبالتالي تقليل حدوث الملاءمة الزّائدة و يمكن اعتبار أن أفضل أقصى عمق عند النّقطة 7.

clf_2 = RandomForestClassifier(n_estimators=50, bootstrap=True, random_state=0,
                                min_samples_split=10, min_samples_leaf=10)
clf_2.fit(X_train, y_train)
# Number of folds for cross validation
num_folds = 10
plot_validation_curve(clf_2, X_train, y_train, param_name='max_depth', param_range=range(2,13))

الخاتمة

تعرّفنا في هذه المقالة على مفهومين مهمّين في مجال تعلّم الآلة، هما الملاءمة الزّائدة والملاءمة الضّعيفة و أسباب حدوث كلّ منهما و طرق الكشف عنهما، كذلك طرق تجنّبهما أثناء تدريب نماذج تعلّم الآلة.

ويمكننا تلخيص أهمّ ما تعلّمناه في مقالتنا في ثلاث نقاط:

• التّعميم هو أن يكون النّموذج قادرًا على التنبّؤ بشكل دقيق بناءً على بيانات الاختبار test data وهي بيانات جديدة غير مرئيّة، أي لم يتدرّب عليها النّموذج، و يكون لها نفس خصائص مجموعة التّدريب train data، و إذا كان النّموذج  غير قادر على التّعميم بشكل جيّد، فمن المحتمل ظهور مشكلة الملاءمة الزّائدة أو الملاءمة الضّعيفة.
• يكون النّموذج ذا ملاءمة ضعيفة عندما لا يكون قادرًا على إجراء تنبّؤات دقيقة حول بيانات التّدريب، كما أنّه لا يمتلك القدرة على التّعميم بشكل جيّد على البيانات الجديدة. تحدث الملاءمة الضّعيفة عادةً عندما نتعامل مع النّماذج الخطّيّة، ويمكن منعه عن طريق تدريب نماذج  أكثر تعقيدًا، زيادة وقت التّدريب، إزالة الضّوضاء من البيانات و ضبط معاملات التّنظيم.
• يكون  النّموذج ذا ملاءمة زائدة عندما يفشل في الأداء الجيّد على بيانات الاختبار، على عكس بيانات التّدريب فإنّه يؤدّي أداء جيّدًا. يوجد العديد من التّقنيات للحدّ من الملاءمة منها: زيادة البيانات ،التّوقّف المبكّر، تعزيز البيانات ،إزالة المزايا ،التّنظيم، التّجميع ، وغيرها .

إذا كنت ترغب في رؤية الشّيفرات البرمجيّة كاملة، يمكنك العثور عليها على مستودع الشيفرة البرمجيّة غيت-هب عبر هذا الرّابط.

المراجع

• [1]:Techniques for handling underfitting and overfitting in Machine Learning
• [2]:ML | Underfitting and Overfitting
• [3]:Overfitting and Underfitting in Machine Learning
• [4]:Overfitting and underfitting in machine learning
• [5]:Example of overfitting and underfitting in machine learning