التدقيق العلمي: د. م. حسن قزّاز، م. رامي عقّاد
التّدقيق اللغوي: هبة الله فلّاحة
المَحتويَات
يُعدّ التمثيل المرئيّ للبيانات Data Visualization عنصرًا أساسيًّا في تحليل البيانات Data Analysis، حيث أنّها تُفيد في إيصال المعلومات بشكل أبسط و أسرع؛ فهي تتمتّع بقدرتها على تلخيص كمّيّات كبيرة من البيانات بكفاءة من خلال مخطّط بيانيّ، ولا تكاد أيّ مجموعة بيانات تخلو من البيانات الكمّيّة Quantitative Data التي تحتاج إلى تحليل و عمل تمثيل مرئيّ لاستنباط المعلومات اللّازمة منها.
في هذه المقالة، سنتحدّث عن البيانات الكمّيّة و أنواعها، و المخطّطات التي تُستخدم في التّمثيل المرئيّ للبيانات الكمّيّة وهي ما يلي:
- مخطّط الصّندوق (Box Plot)
- المُدرّج التّكراريّ (Histogram)
- مخطّط الانتشار (Scatterplot)
- مخطّط الكمان (Violin Plot)
- المخطّط الخطّيّ (Line Graph)
سنستخدم في مقالتنا مجموعة البيانات Datatset الخاصّة بالحبوب الغذائيّة، بإمكانك إيجادها في موقع كاجل Kaggle عبر هذا الرّابط ، لاستخدامها في عرض المخطّطات المختلفة. إذا كنت ترغب في تشغيل الشّيفرة البرمجيّة أدناه، فستحتاج إلى تنزيل مجموعة البيانات وحفظها، ثمّ قم بتشغيل الشّيفرة البرمجيّة [1]:
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
df = pd.read_csv('/content/cereal.csv')
df['cal_per_cup'] = df.calories/df.cups # adding column to look at calorie content per cup rather than per serving
ما هي المتغيّرات الكمّيّة (العدديّة) Quantitative Variable ؟
هي المتغيّرات التي يمكن قياسها وتسجيلها بصورة رقميّة، مثل الوزن، الطّول، السّعرات الحراريّة والعمر. وتنقسم إلى نوعين أساسيّن هما:
-
المتغيّر الكمّيّ المنفصل (Discrete Quantitative variable)
هي المتغيّرات التي تأخذ قيمًا قابلة للعدّ، ولها عدد محدود من القيم و غالبًا ما تكون القيم أعدادًا صحيحة.
أفضل طريقة لمعرفة ما إذا كانت مجموعة البيانات تُمثّل متغيّرات كمّيّة منفصلة؛ هي عندما تكون المتغيّرات قابلة للعدّ ويكون عدد الاحتمالات محدودًا.
على سبيل المثال عندما تُحسب عدد الأهداف المُسجّلة في لعبة رياضيّة أو عدد مرّات رنين الهاتف، فهذا متغيّر كمّيّ منفصل [2].
-
المتغيّر الكمّيّ المستمرّ (Continuous Quantitative variable)
هي المتغيّرات التي لا يمكن عدّ قيمها.
على سبيل المثال: عندما تقيس حجم الماء في الخزّان أو درجة حرارة المريض، فهذا متغيّر كمّيّ مستمرّ[2].
طرق التّمثيل المرئيّ لبيانات المُتغيّرات الكمّيّة(Quantitative Variable):
مخطّط الصّندوق (Box Plot)
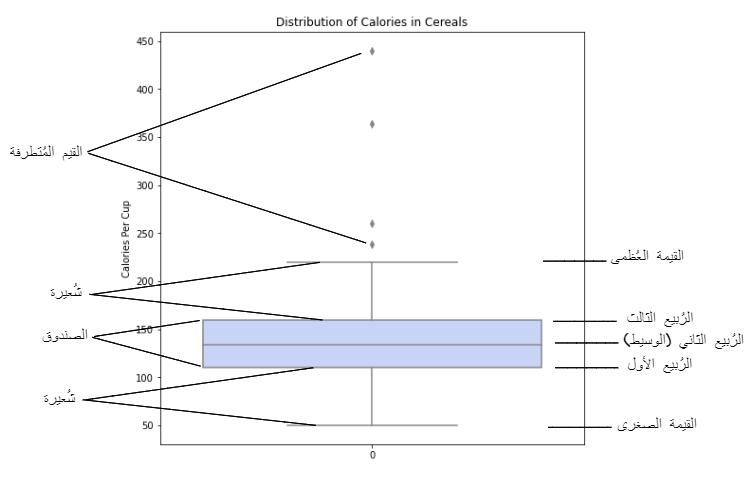
هو مخطّط على شكل صندوق يمكن رسمه بشكل أفقيّ أو بشكل عاموديّ، كما هو موضّح في الشّكل (1) يتمّ تمثيل عيّنة البيانات الكمّيّة من خلال تمثيل القيم الإحصائيّة الخمس : القيمة الصّغرى(Minimum)، الرُّبيع الأوّل Q1، الرُّبيع الثّاني (الوسيط) Median، الرُّبيع الثّالث Q3، والقيمة العظمى(Maximum).

يُساعد المخطّط الصّندوقيّ مُحلّل البيانات على فهم مجموعة البيانات بشكل أعمق. فيما يلي أهمّ أهداف استخدام المخطّط الصّندوقيّ [3] :
- يُعدّ مخطّط الصّندوق مفيدًا لأنّه يعرض الوسيط لمجموعة البيانات. الوسيط (Median) هو القيمة المتوسّطة من مجموعة من البيانات ويظهر بالخطّ المستقيم الذي يقسم المربّع إلى جزأين، وتكون نصف القيم أكبر من هذه القيمة أو مساوية لها والنّصف الآخر أقلّ.
- يُعدّ مخطّط الصّندوق مفيدًا لأنّه يعرض انحراف مجموعة البيانات، حيث يظهر شكل الرّسم المربّع إذا كانت مجموعة البيانات الإحصائيّة موزّعة بشكل طبيعيّ Normal Distribution أو منحرفة Skewed.
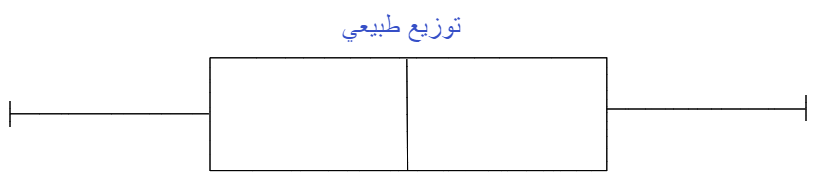
كما في الشّكل(2) عندما يكون الوسيط في منتصف الصّندوق والشّعيرات whiskers على جانبي الصّندوق متماثلة تقريبًا، يكون التّوزيع طبيعيًّا.
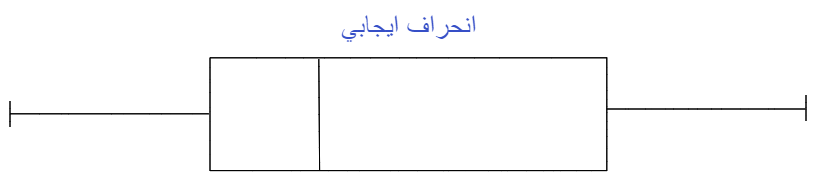
وكما في الشّكل (3)عندما يكون الوسيط أقرب إلى أسفل الصّندوق، وإذا كانت الشّعيرة أقصر في الطّرف السّفليّ من المربّع، فإنّ التّوزيع يكون منحرفًا بشكل إيجابيّ Positive Skewed (منحرف إلى جهة اليمين).
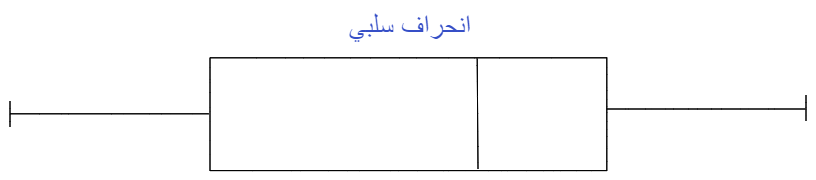
وكما في الشّكل (4) عندما يكون الوسيط أقرب إلى الجزء العلويّ من المربّع، وإذا كانت الشّعيرة أقصر في الطّرف العلويّ من المربّع، فإنّ التّوزيع يكون منحرفًا بشكل سلبيّ Negative Skewed(منحرف إلى جهة اليسار).
3. المخطّط الصّندوقي مفيد لأنّه يُظهر تشتّت مجموعة البيانات في الإحصاء؛ التّشتّت _ويسمّى أيضًا الانتشار_ هو مدى تمدّد أو ضغط التّوزيع.
توجد أصغر قيمة Minimum وأكبر قيمة Maximum في نهاية الشّعيرات وهي مفيدة لتوفير مؤشّر مرئيّ فيما يتعلّق بانتشار القيم.
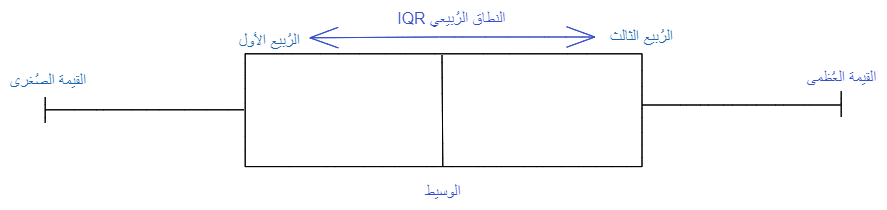
النّطاق الرّبيعيّ (IQR) هو مخطّط الصّندوق الذي يظهر متوسّط 50٪ من الدّرجات، ويمكن حسابه عن طريق طرح الرّبع السّفليّ من الرّبع العلويّ (على سبيل المثال Q3 − Q1) كما هو موضّح في الشّكل(5).
4. المخطّط الصّندوقيّ مفيد لأنّه يعرض القيم المتطرّفة داخل مجموعة البيانات؛
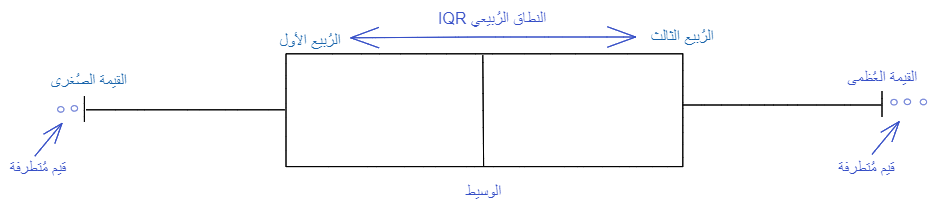
القيم المُتطرّفة outliers هي قيم بعيدة عدديًّا عن بقية البيانات، ويمكن وصفها على أنّها نقاط البيانات الواقعة خارج شُعيرات مخطّط الصّندوق كما هو موضّح في الشّكل(6).
سنستخدم لرسم المخطّط الصّندوقيّ مكتبة سيبورن seaborn، حيث يتمّ الرّسم من خلال استدعاء تابع رسم المخطّط الصّندوقيّ boxplot، وتمرير مجموعة البيانات مع تحديد اسم المتغيّر المُراد تمثيله [1].
يمتلك تابع المخطّط الصّندوقيّ العديد من المعاملات منها: المعامل orient لتحديد اتجاه الصّندوق، فيمكن أن يكون أفقيًّا ويرمز له بالقيمة “h” أو عموديًّا ويرمز له بالقيمة “v”، أمّا المُعامل color فهو لتحديد لون المخطّط الصّندوقيّ ويوجد غيرها الكثير من المعاملات الأخرى.
لاحظ في الشّيفرة البرمجيّة للرّسم البيانيّ أدناه، إنّ المُعاملات الافتراضيّة للرّسم البيانيّ لا تُعيّن نهايات الشّعيرات على القيمة العظمى والقيمة الصّغرى؛ لعمل ذلك يجب إسناد قيمة الفرق بين القيمة العظمى والقيمة الصّغرى للمعامل whis، حيث أنّ قيمته الافتراضيّة تكون 1.5 ونتيجة تنفيذ الشّيفرة البرمجيّة السّابقة موضّحة في الشّكل(7).
#find range
range_cal_per_cup = df.cal_per_cup.max() - df.cal_per_cup.min()
plt.figure(figsize=(8, 8))
sns.boxplot(data=df, y='cal_per_cup', orient="v", color='#BFD0FE', whis=range_cal_per_cup)
plt.ylabel('Calories Per Cup')
plt.title('Distribution of Calories in Cereals');
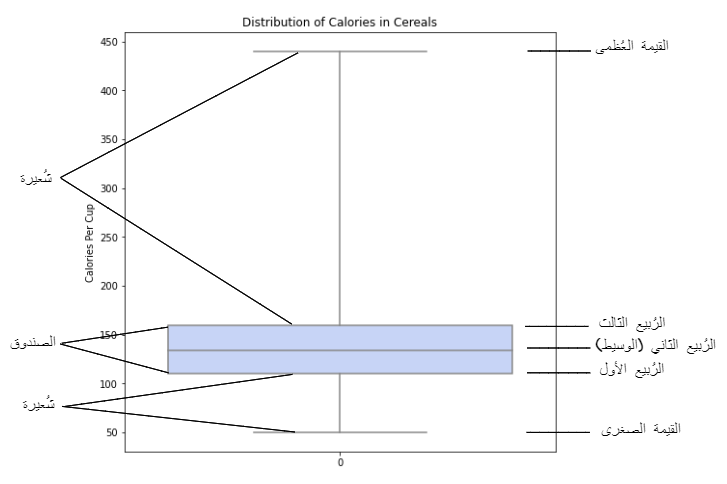
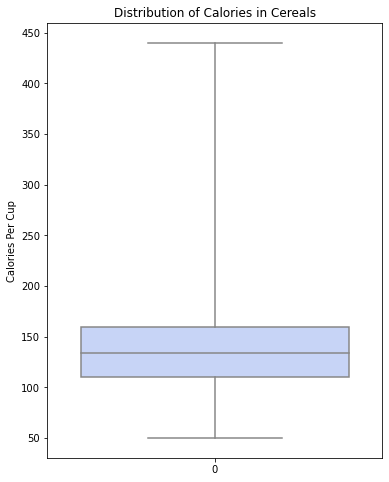
في الوضع الافتراضيّ تكون نهاية الشّعيرة العلويّة تشير الى أكبر نقطة ضمن (1.5 * النّطاق الرّباعيّ (IQR))، حيث يشير معدّل(IQR) إلى الفرق بين قيمة الرّبيع الثّالث و قيمة الرّبيع الأوّل.
هذا يعني أنّ نهاية الشّعيرة العلويّة تكون عند أعلى نقطة بيانات أقلّ من 1.5 * IQR وتكون أعلى من الرّبيع الثّالث Q3، و يتمّ وضع نهاية الشّعيرة السّفليّة عند أدنى نقطة ضمن 1.5 * IQR، و يتمّ رسم أيّ نقاط خارج نطاق هاتين العلامتين على أنّها قيم مُتطرّفة كما هو موضّح في الشّكل (8).
plt.figure(figsize=(8, 8))
sns.boxplot(data=df, y='cal_per_cup', orient="v", color='#BFD0FE')
plt.ylabel('Calories Per Cup')
plt.title('Distribution of Calories in Cereals');
تعتبر المخطّطات الصّندوقيّة رائعة لفهم انتشار وانحراف مجموعة البيانات، إذا كنت ترغب في إظهار عدّة توزيعات وكيفيّة مقارنتها في وقت واحد، فإنّ مخطّطات الصّندوق هي طريقة رائعة للقيام بذلك [2].
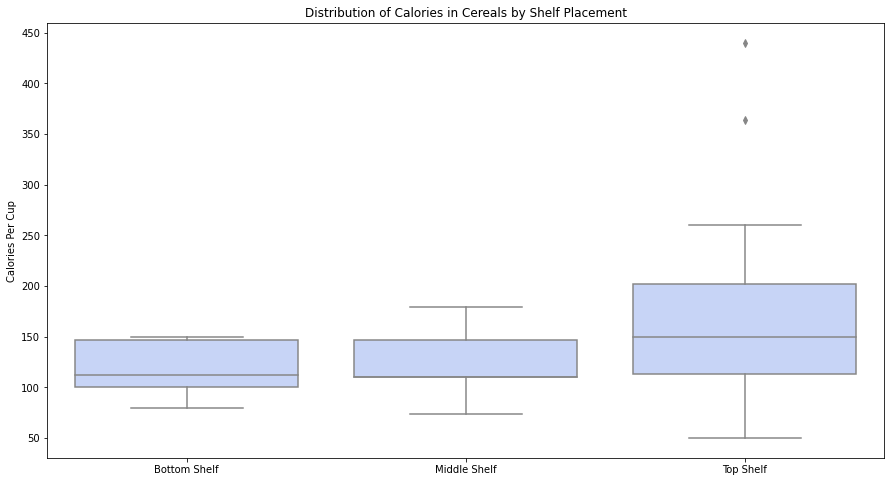
على سبيل المثال الشّكل (9) يوضّح توزيع السّعرات الحراريّة لكلّ كوب من الحبوب مقسومًا على الرّفّ الموجود على الحبوب.
من خلال تقسيم البيانات إلى فئات لوضع الرّفّ، يمكننا أن نرى بسرعة أنّ جميع القيم المتطرّفة في مخطّط الصّندوق جاءت من الحبوب الموجودة على الرّفّ العلويّ، ويوضّح أيضًا أنّ الرّف العلويّ لا يحتوي فقط على أعلى متوسّط لعدد السّعرات الحراريّة وأكبر قيمة عظمى من السّعرات الحراريّة، ولكنّه يشتمل أيضًا على أقلّ قيمة صغرى من السّعرات الحراريّة [1].
plt.figure(figsize=(15, 8))
sns.boxplot(data=[df[df.shelf==1].cal_per_cup, df[df.shelf==2].cal_per_cup, df[df.shelf==3].cal_per_cup],
orient='v', color='#BFD0FE')
plt.xticks([0,1,2], ['Bottom Shelf', 'Middle Shelf', 'Top Shelf'])
plt.ylabel('Calories Per Cup')
plt.title('Distribution of Calories in Cereals by Shelf Placement');
المُدرّج التّكراريّ (Histogram)
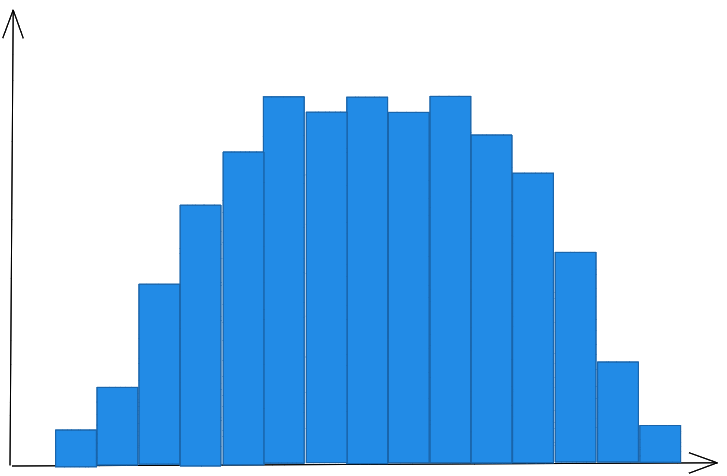
هو مخطّط يتكوّن من مجموعة من الإبر المتلاصقة مختلفة الأطوال كما هو في الشّكل (10)، حيث تمثّل التّكرارات على المحور الرّأسيّ Y- axis، بينما تمثّل قيم المتغيّر ( حدود الفئات) على المحور الأفقيّ X- axis، ويتمّ تمثيل كلّ فئة بعمود bar، ارتفاعه هو تكرار الفئة، وطول قاعدته هو طول الفئة، ويمكن رسمه بشكل أفقيّ أو بشكل عموديّ .
حيث يوضّح المدرّج التّكراريّ توزيع البيانات الكمّيّة المتّصلة ومدى تركيزها أو تشتّتها، ويستخدم في الإحصاء statistics ليوضّح إن كانت البيانات تتوزّع بشكل طبيعيّ (Normal Distribution) أم لا.
يُساعد المُدرّج التّكراريّ محلّل البيانات على فهم مجموعة البيانات بشكل أعمق، فيما يلي أهمّ أهداف استخدام المُدرّج التّكراريّ[4] :
- إعطاء تقدير لمكان تركيز القيم، وماهيّة النّهايات وما إذا كانت هناك أي فجوات أو قيم متطرّفة.
- إعطاء عرض تقريبيّ لتوزيع القيم.
- تحديد إن كانت البيانات متوزّعة بشكل طبيعيّ أو يوجد بها انحراف، وتحديد اتّجاهه إن وُجد.
توزّع البيانات في المدرّج التّكراريّ Histogram
- التوزّع الطّبيعيّ Normal Distribution: يتمّ توزّع البيانات وتتمحور حول قيمة المتوسّط، كما هو موضّح في الشّكل (11) أدناه.

2. التوزّع ثنائيّ النّسق Bimodal distribution: يكون فيه توزّع البيانات على شكل قمتين، يتمّ التّعامل مع كلّ واحدة منهما على حدة و تحليلها كتّوزيعات طبيعيّة. كما هو موضّح في الشّكل (12) أدناه.

3. التّوزّع المنحرف لليمين Right-skewed distribution: يسمّى أيضًا التوزّع المنحرف بشكل إيجابيّ، في التّوزّع المنحرف لليمين يكون عدد كبير من قيم البيانات على الجانب الأيسر، و عدد أقلّ من قيم البيانات على الجانب الأيمن، كما هو موضّح في الشّكل (13) أدناه.

4. التوزّع المنحرف لليسار left-skewed distribution: يسمّى أيضًا توزعًا منحرفًا سالبًا، في التوزّع المنحرف إلى اليسار يكون عدد كبير من قيم البيانات على الجانب الأيمن، و عدد أقلّ من قيم البيانات على الجانب الأيسر كما هو موضّح في الشّكل (14) أدناه.

5. التوزّع العشوائيّ Random Distribution: التوزّع العشوائيّ يفتقر إلى نمط واضح وله عدّة قمم، كما هو موضّح في الشّكل (15) أدناه.

لا توجد قواعد محدّدة لحجم وعدد الإبر، لذا من المهمّ التّفكير في عدد الخانات حيث سيؤثّر ذلك على وضوح المدرّج التّكراريّ، على الرّغم من أنّ أدوات التّصوّر تتضمّن معايير الاختيار الخاصّة بهم لهذه المعلمات، فمن الضّروري تجربة القيم الأخرى، فيمكن اقتراح عدد الفواصل الزّمنيّة حسب طبيعة مجموعة البيانات .
ضع في اعتبارك دائمًا أنّ: فترات قليلة لا تسمح لنا بتوضيح البنية الدّقيقة لتوزيع البيانات.
سنستخدم لرسم المخطّط الصّندوقيّ مكتبة الرَّسم الرِّياضيّ في بايثون (ماتبلوت)(matplotlib)، حيث يتمّ الرّسم من خلال استدعاء تابع هيست hist، وتمرير مجموعة البيانات مع تحديد اسم المتغيّر المُراد تمثيله[1].
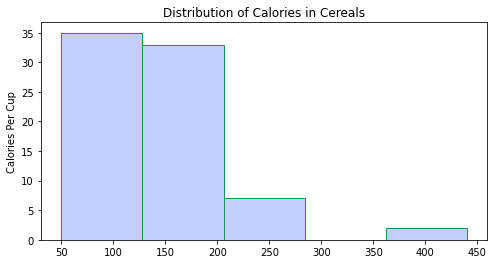
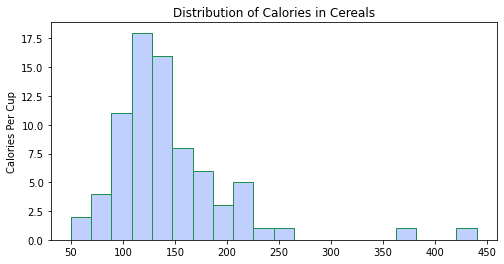
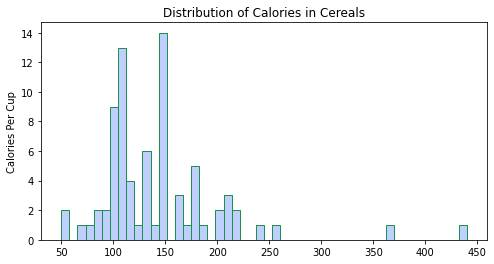
في الشّيفرة البرمجيّة أدناه، قمت بتعيين عدد الإبر bins على 5 كما هو موضّح في الشكل(16)، ثمّ 20 كما هو موضّح في الشكل(17)، ثمّ 50 كما هو موضّح في الشكل(18).
ملاحظة: بالنّسبة لمجموعة البيانات هذه، قامت 20 حاوية بتمثيل البيانات بشكل جيّد، ومع ذلك لا توجد قاعدة صارمة وسريعة لعدد الصّناديق التي يجب عليك استخدامها، وقد يكون 20 سيّئًا لمجموعة البيانات الخاصّة بك. يجب تجربة عدد مختلف من الحاويات وتحديد الرّقم الذي ينقل انتشار القيم بشكل أكثر وضوحًا[1].
plt.figure(figsize=(8, 4))
plt.hist(df.cal_per_cup, bins=20, color='#BFD0FE', edgecolor='#1F8F50')
plt.ylabel('Calories Per Cup')
plt.title('Distribution of Calories in Cereals');
مخطّط الانتشار (Scatterplot)
مخطّط الانتشار هو مخطّط ارتباط يُستخدم للبحث في العلاقة بين متغيّرين أو ثلاثة متغيرات، إحداهما مستقلّ والآخر تابع، وبعد تحديد هذه العلاقة يمكن التنبّؤ بسلوك المتغيّر التّابع استنادًا على تغيّرات المتغيّر المستقلّ.
يُرسم المتغيّر المستقلّ عادةً على المحور الأفقيّ (X-axis)، والمتغيّر التّابع على المحور الرأسي (Y-axis)، ثمّ تُحدّد القيم المختلفة للمتغيّر المستقلّ، ويُسجّل التّغيير الحاصل على المتغيّر التابع على مخطّط الانتشار.
قد تُظهر النّتائج عدم وجود ارتباط بين المتغيّرين، أو قد يظهر ارتباط معتدل أو قويّ بينهما، و إذا أظهر المخطّط وجود علاقة، فهذا لا يعني دومًا أنّ أحد المتغيّرات تسبّب في الآخر، من الممكن أن يكون تأثّر كلاهما بمتغيّر ثالث.
كلما كان مخطّط الانتشار مشابهًا لخطّ مستقيم، كانت العلاقة بين المتغيّرات أقوى، ،و تُعرف النّقاط التي تكون بعيدة عن المجموعة العامّة للنّقاط بالقيم المتطرّفة.
أنواع الارتباط correlation في مخطّط الانتشار:
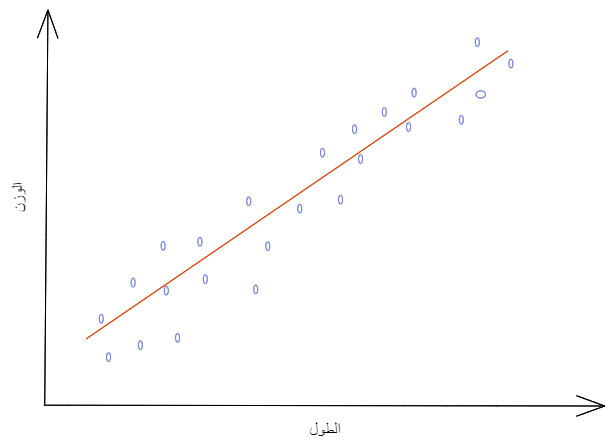
- الارتباط الإيجابيّ Positive Correlation: كلما تزداد قيمة المتغيّر المستقلّ تزداد قيمة المتغيّر التّابع.
كما هو موضّح في الشّكل (19) فكلما زاد طول الانسان زاد وزنه (علاقة طرديّة).
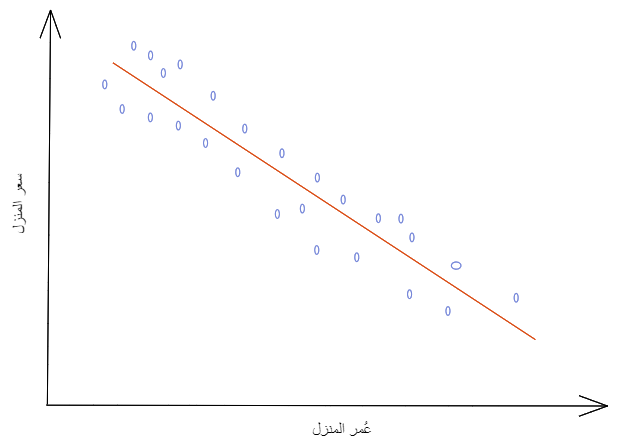
- الارتباط السّلبيّNegative Correlation: كلما تزداد قيمة المتغيّر المستقلّ تتناقص قيمة المتغيّر التّابع.
كما هو موضّح في الشّكل (20) فكلما زاد عمر المنزل انخفض سعره(علاقة عكسيّة).
- لا يوجد ارتباط No correlation: لا يوجد علاقة بين المتغيّرين كما هو موضّح في الشّكل (21).

يُساعد مخطّط الانتشار محلّل البيانات على فهم مجموعة البيانات بشكل أعمق، فيما يلي أهمّ أهداف استخدام مخطّط الانتشار :
- إيجاد الارتباطات بين البيانات وتحديد نوعها.
- إظهار كافّة نقاط البيانات بما في ذلك الحدّ الأدنى والحدّ الأقصى والقيم المتطرّفة.
سنستخدم لرسم المخطّط الصّندوقيّ مكتبة سيبورن (seaborn)، حيث يتمّ الرّسم من خلال استدعاء تابع رسم مخطط الانتشار scatterplot وتمرير مجموعة البيانات مع تحديد اسم المتغيّر المُراد تمثيله.
plt.figure(figsize=(8, 4))
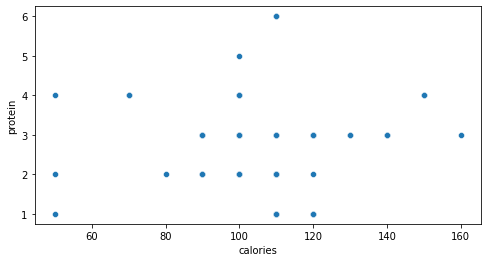
sns.scatterplot(data=df, x='calories', y='protein')
plt.xlabel('calories')
plt.ylabel('protein')
ويكون شكل الخرج كما هو موضّح في الشّكل (22):
مخطّط الكمان (Violin Plot)
هو نوع من الرّسم البيانيّ يشبه الكمان، يستخدم هذا النوع من الرّسم البيانيّ لعرض التوزّع والكثافة الاحتماليّة للبيانات، ويمكن اعتباره مزيجًا من مخطّط الصّندوق Box plot و مخطّط الكثافة (Kernel Density plot (KDE .
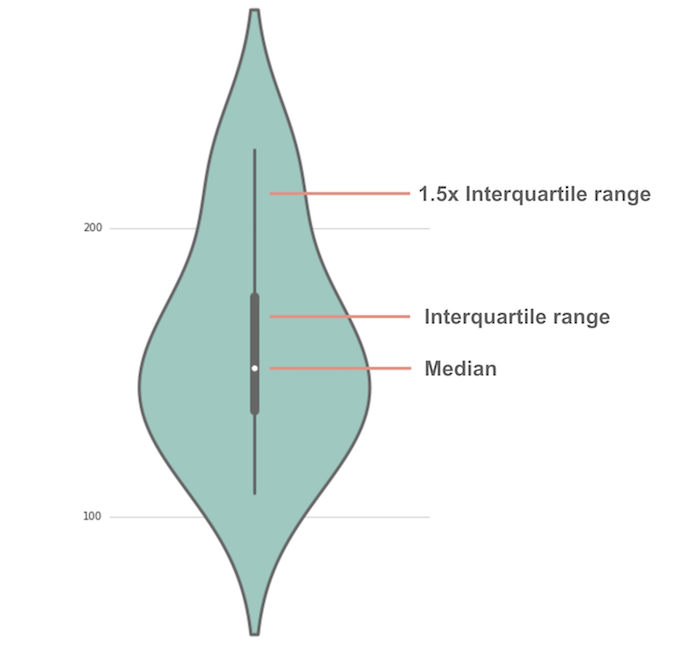
يوضّح الشّكل (23) مخطّط الكمان Violin plot، حيث تمثّل النّقطة البيضاء الوسيط و يمثّل الشّريط الرّماديّ السّميك في الوسط النّطاق الرّبيعيّ IQR، ويمثّل الخطّ الرّماديّ الرّفيع بقيّة التّوزيع باستثناء النّقاط التي تمّ تحديدها على أنّها قيم متطرّفة[5].
سنستخدم لرسم المخطّط الصّندوقيّ مكتبة سيبورن (seaborn)، حيث يتمّ الرّسم من خلال استدعاء تابع رسم مخطط الكمان violinplot وتمرير مجموعة البيانات مع تحديد اسم المتغيّر المُراد تمثيله[1].
plt.figure(figsize=(4, 8))
sns.violinplot(data=df.cal_per_cup, color='#BFD0FE', orient='v')
plt.ylabel('Calories Per Cup')
plt.title('Distribution of Calories in Cereals');
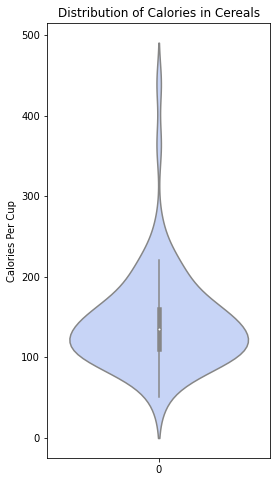
ويكون شكل الخرج كما هو موضّح في الشّكل (24):
- مثل مخطّطات الصّندوق تعدّ مخطّطات الكمان رائعة لعرض عدّة مجموعات من البيانات جنبًا إلى جنب لمقارنة مجموعتين من البيانات، شاهد البيانات مقسّمة حسب وضع الرّف مرّة أخرى أدناه:
plt.figure(figsize=(15, 8))
sns.violinplot(x=df.shelf, y=df.cal_per_cup, color='#BFD0FE')
plt.xticks([0,1,2], ['Bottom Shelf', 'Middle Shelf', 'Top Shelf'])
plt.xlabel('Cereal Placement', fontsize=16)
plt.ylabel('Calories Per Cup', fontsize=16)
plt.title('Distribution of Calories in Cereals by Shelf Placement', fontsize=20)
plt.tight_layout();
ويكون شكل الخرج كما هو موضّح في الشّكل (25):
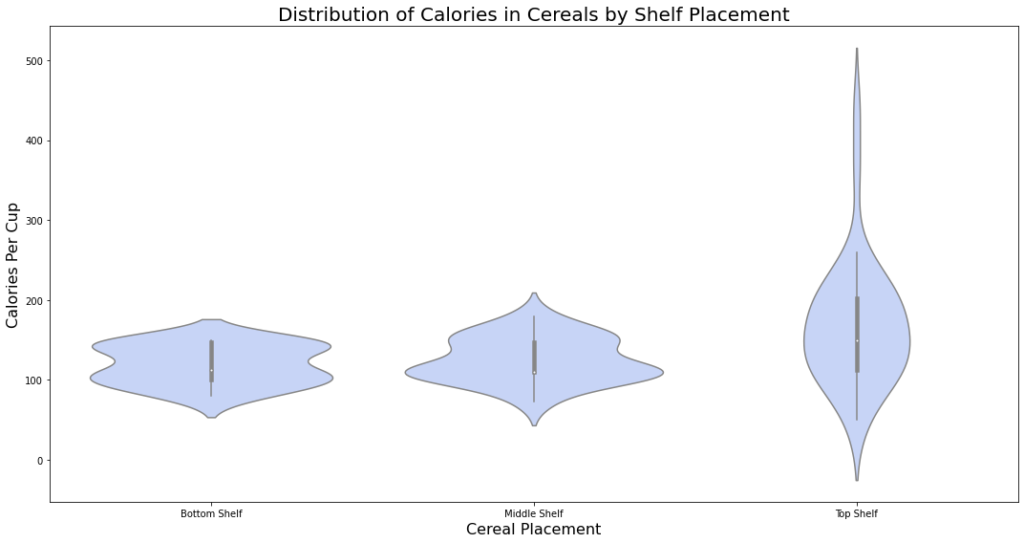
ميزة أخرى رائعة لمخطّطات الكمان؛ هي أنّه إذا كان لديك فئة ثنائيّة ترغب في عرض بياناتك بها، فيمكنك تقسيم مخطّط الكمان لإظهار مخطّط الكثافة لمجموعة واحدة من البيانات على اليسار، و مجموعة أخرى من البيانات على اليمين، يعرض القسم الأوسط الوسيط والقيم الأخرى للبيانات المجمّعة [1].
plt.figure(figsize=(15, 8))
plot = sns.violinplot(x=df[(df.mfr == 'K') |(df.mfr == 'G')].shelf,
y=df[(df.mfr == 'K') |(df.mfr == 'G')].cal_per_cup,
hue=df[(df.mfr == 'K') |(df.mfr == 'G')].mfr,
split=True, color='#BFD0FE')
handles, labels = plot.get_legend_handles_labels()
plt.xticks([0,1,2], ['Bottom Shelf', 'Middle Shelf', 'Top Shelf'])
plt.ylabel('Calories Per Cup', fontsize=16)
plt.xlabel('Cereal Placement', fontsize=16)
plt.legend([handles[0], handles[1]], ['Kelloggs', 'General Mills'], title='Manufacturer')
plt.title('Distribution of Calories in Cereals \nby Shelf Placement and Manufacturer', fontsize=20)
plt.tight_layout();
ويكون شكل الخرج كما هو موضّح في الشّكل (26):
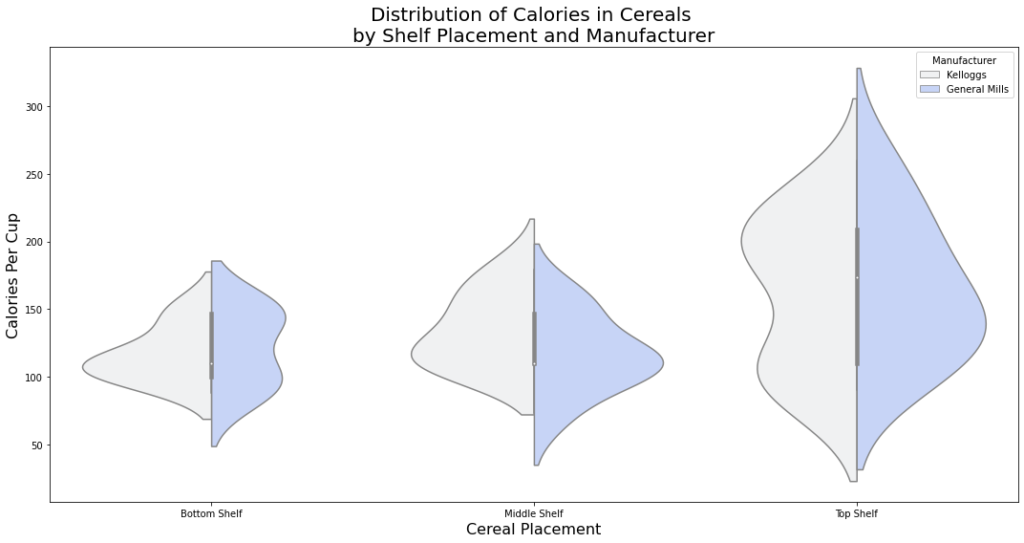
يوضّح الرّسم البيانيّ أعلاه السّعرات الحراريّة لكلّ كوب مع تقسيم البيانات إلى الحبوب التي تنتجها شركة جنرال ميلز General Mills، والحبوب التي تنتجها Kelloggs (الشّركات المصنّعة لغالبيّة الحبوب في مجموعة البيانات).
المخطّط الخطّيّ (Line Graph)
عبارة عن خطّ أو منحنى يربط سلسلة من نقاط البيانات الكمّيّة تسمى “علامات” على الرّسم البيانيّ، ويعتبر المخطّط الخطّيّ شبيهًا بمخطّط الانتشار(Scatter Diagram)، إلّا أنّ الاختلاف يكمن في طريقة ترتيب النّقاط البيانيّة والطّريقة التي يتمّ فيها وصل العلامات بخطوط مستقيمة.
ويستخدم هذا النّوع غالبًا لتصويرالاتّجاه أو التّغيّر الذي يطرأ على البيانات الكمّيّة خلال فترات زمنيّة قصيرة أو طويلة.
سنستخدم لرسم المخطّط الصّندوقيّ مكتبة سيبورن (seaborn)، حيث يتمّ الرّسم من خلال استدعاء تابع رسم المخطّط الخطّيّ lineplot، وتمرير مجموعة البيانات مع تحديد اسم المتغيّر المُراد تمثيله.
plt.figure(figsize=(15,10))
sns.lineplot(x='rating',y='calories', data=df, label='Calories')
plt.title("Calories-Rating line plot", fontsize = 20)
plt.xlabel('Rating', fontsize=20)
plt.ylabel('calories', fontsize=20)
plt.legend()
ويكون شكل الخرج كما هو موضّح في الشّكل (26):
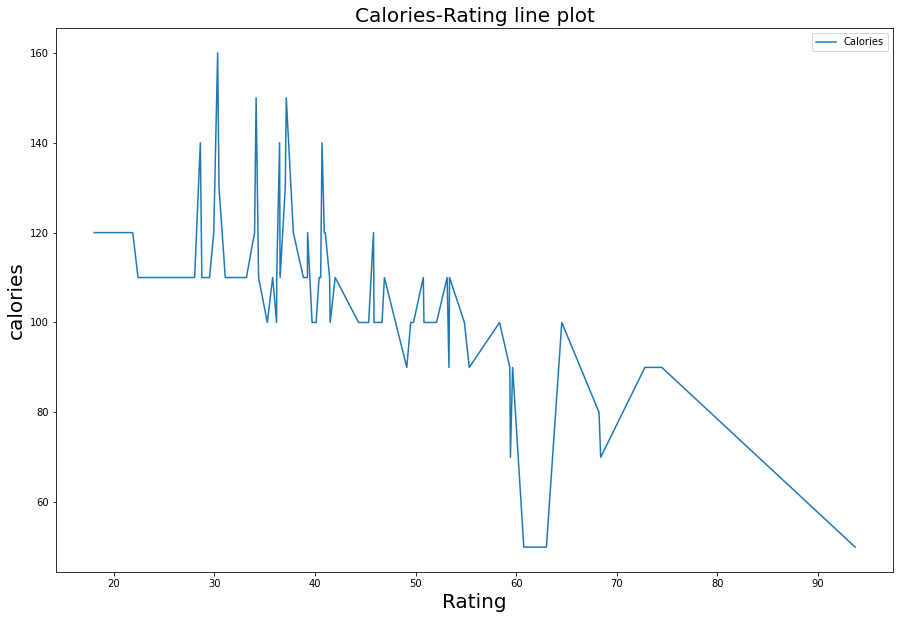
الخاتمة
تعرّفنا في هذا المقال على البيانات الكمّيّة وطرق تمثيلها باستخدام مكتبات البايثون، وهي مخطّط الصّندوق Box plot، مخطّط المدرّج التّكراريّ Histogram، مخطّط الانتشار Scatter plot، مخطّط الكمان Violin plot و أخيرًا المخطّط الأفقيّ Line plot.
إذا كنت ترغب في رؤية الشّيفرات البرمجيّة كاملة، يمكنك العثور عليه هنا.