طرق حساب التشابه بين المستندات النصية Methods for calculating similarity between text documents

المقدّمة Introduction

إنّ محرّكات البحث يتمّ تصميمها للبحث عن المستندات ذاتِ العلاقة فيما بينها، من خلال البحث عن كلماتٍ مشابهة أو مطابقة، ذلك أنّ المستخدم يقوم بإدخال كلماتٍ مفتاحية في الاستعلام المعين،  ثمّ يقوم النظام بالبحث عن كلّ المستندات التي تحتوي الكلمات المفتاحيّة ويتمّ عرضها على المستخدم، ومن أجل تحقيق هذا الهدف هناك العديد من الخوارزميّات المستخدَمة في محرّكات البحث لتحقيق أفضل النتائج

في هذا المقال سوف نتعرّف على اثنين من أفضل الطرق المستخدمة في البحث عن المستندات ذاتِ العلاقة و تُعرف الأولي بخوارزميّة تشابه-جيب التّمام والثانية بتقنية التردد العكسي (Inverted Index).

إنّ مقياس تشابه-جيب التّمام هو عبارة عن حساب جيب تمام الزّاوية بين متجهَين، ويُستخدم هذا المقياس في علم البيانات على سبيل المثال لا الحصر مع البيانات النصيّة  لمعرفة مدى تطابق النّصوص مع بعضها البعض في عمليات البحث، وهناك العديد من محرّكات البحث مثل غوغل (google) و بينغ (Bing) التي تستخدم هذا المقياس في إيجاد الكلمات المطابقة في النصوص، والتي تشابه الكلمات في الاستعلام على المواقع الإلكترونية، بالإضافة إلى استخدامه في عملياتِ استرجاعِ البيانات واكتشاف عمليات السّرقات الأدبيّة والعديد من الاستخدامات الأخرى.وفي ذات السياق تستخدم تقنية التردد العكسي لتحسين وزيادة سرعة عمليات البحث على وجه الخصوص مع البيانات الضخمة,وفي هذا المقال عزيزي القارئ سوف نتطرق بالشرح المفصل لكلا الطريقتين.

المحتويات Outline

1. المقدّمة
2. تعريف ماهو تشابه-جيب التّمام(cosine Similarity)
3. مكتبةُ الرَّسمِ الرِّياضيِّ في بايثون (matplotlib)
4. مكتبةُ تحليلِ البياناتِ في بايثون (pandas)
5. تطبيق عمليّ على بيانات رقميّة
6. تطبيق عمليّ على بيانات نصيّة
7. التردد العكسي
8. الخاتمة
9. المراجع

تعريف ماهو تشابه-جيب التّمام cosine Similarity

تشابه-جيب التّمام هو عبارةٌ عن مقياسٍ من خلاله نستطيع أن نحدّد مدى تطابق المستندات بغضّ النظر عن حجمها، ورياضيّاً هو عبارة عن مقياس جيب تمام الزّاوية cosine بين متجهَين في فضاءٍ ثنائيّ الأبعاد، ويمكن أن يكون هذان المتجهَان عبارةً عن بياناتٍ رقميّة أو نصيّة.

وسوف نقوم في هذا المقال بالتعرّف على هذه البيانات وكيفية تطبيق خوارزميّة تشابه -جيب التمام على كلا النوعَين من خلال أمثلة عمليّة.

ولكن في البداية سوف نتعرّف على بعض المكتبات التي من خلالها نستطيع القيام بالتطبيق العمليّ، فهي تحتوي على العديد من الأصناف(Classes) والدوال التي سوف يتمّ استخدامها في الأمثلة العمليّة.

مكتبةُ الرَّسمِ الرِّياضيِّ في بايثون matplotlib

هي عبارة عن مكتبةٍ مفتوحةِ المصدر في بايثون، تُستخدم لإنشاء أشكال(Figures) مختلفةِ لتصوير البيانات(Data Visualization)، وقد تكون هذه الأشكال ثابتة متحرّكة أو تفاعلية، وهي تعتمد على الدوال الموجودة في مكتبة بايثون العدديّة (Numpy) للتعاملِ مع البيانات الرّقمية المصفوفات متعدّدة الأبعاد.

مكتبةُ تحليلِ البياناتِ في بايثون pandas

هي عبارة عن مكتبةٍ مفتوحةِ المصدر مجانيّة، يتمّ استخدامها في معالجة وتحليل البيانات وتعلّم الآلة (Machine Learning)وتعتمد هذه المكتبة على مكتبةٍ أخرى هي مكتبة بايثون العدديّة، والتي تساعد في التعامل مع الأرقامِ المصفوفات ذاتِ البعد الواحد و المصفوفات متعدّدة الأبعاد.

في حال عدم توفر هذه المكتبة يجب تثبيتها أولاً ثمّ استيرادها:

pip install pandasa
import pandas as pd

المفهوم الرّياضي لتشابه-جيب التّمام Math Behind Cosine Similarity

الشّكل(1) يوضّح الزّاوية بين متجهَين في فضاءٍ ثنائيّ الأبعاد.و تكون الزّاوية مقياساً للتشابه بين متجهَين، إذا كانت قيمةُ جيب التّمام تساوي 1 ذلك يعني أنّ المتجهَين متطابقان وأنّ الزّاوية بينهما تساوي صفراً، وأمّا إذا كانت قيمةُ جيب التّمام أصغرَ من الواحد فهذا يحدّد مدى تقاطع هذَين المتجهَين، وبالتالي نسبياً مدى التشابه بين كلمة البحث والبيانات. 

الشّكل(1)الزّاوية بين متجهَين في فضاءٍ ثنائيّ الأبعاد

المعادلة الرّياضية لحساب تشابه-جيب التّمام هي:

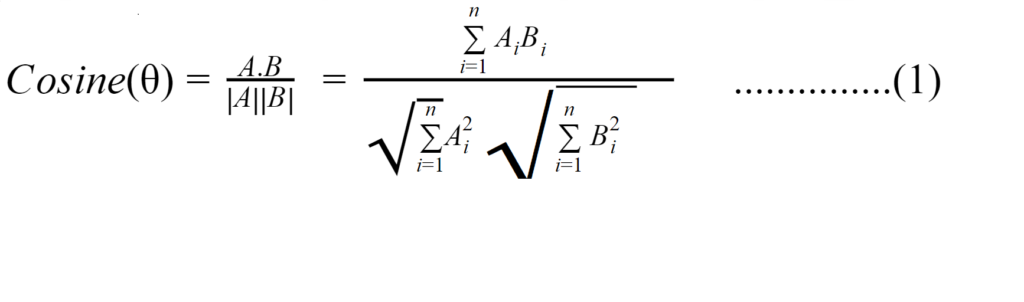
حيث أنّ A ,B هما عبارةٌ عن المتجهَين الذَين نبحث عن تشابهٍ بينهما، و n هي عبارةٌ عن عدد الكلمات في كلّ متجه.

تطبيق عمليّ على بيانات رقميّة Implementation

هنالك طريقتان لحساب جيب التّمام بين متجهَين، أوّلاً عن طريق استخدام المعادلة التي يمثل فيها البسط حاصلَ ضربِ متجهَين، والمقام هو حاصلُ ضرب الجذر التربيعيّ لمجموع مربعات عناصر المتّجهَين كما في المعادلة(1)،وثانياً عن طريق استخدام الدوال المبنيّة داخليّاً (Inbuilt Function)في مكتبة بايثون العدديّة.
التطبيق العمليّ 

سوف نستخدم في هذا المثال متجهاتٍ رقميّة في فضاءٍ ثنائيّ الأبعاد، سوف يكون المتّجه الأوّل (A) والمتّجه الثاني (B)، ومن ثم نحسب تشابه-جيب التمام كما في الشّيفرة البرمجيّة (code) التّالية: 

1.يتطلب العمل توافر مكتبةِ بايثون العدديّة ومكتبةِ الرَّسمِ الرِّياضيِّ في بايثون، في حال عدم توافرهما مُسبقًا على الجهاز يجب تثبيتهما ثمّ استيرادهما:

pip install numpy
pip install matplotlib
Import numpy as np
Import matplotlib.pyplot as plt

2. الآن نستخدم مصفوفاتٍ رقميّة ذاتِ بعدٍ واحد، الأوّل(A) والثاني (B)

A=np.array([7,3])
B=np.array([3,7])

.في هذه الخطوة يتمّ تحويل المصفوفات إلى متجهاتٍ في فضاءٍ ثنائيّ الأبعاد يسمی المتّجه الأوّل (A) والمتّجه الثّاني (B).وفي الشفرة البرمجيّة التالية تمثل: 

دالّة رسم المحاور(axes) هي عبارةٌ عن دالة موجودة في مكتبةُ الرَّسمِ الرِّياضيِّ في بايثون، تستخدم لرسم المحورين الرئيسين (X and Y)
دالّة الترميز (annotate) هي عبارةٌ عن دالة موجودة في مكتبةُ الرَّسمِ الرِّياضيِّ في بايثون، تستخدم لترميز النقاط (x,y) بالكلمات من المستند.
دالّة رسم السهم (arraw) هي عبارةٌ عن دالة موجودة في مكتبةُ الرَّسمِ الرِّياضيِّ في بايثون، تستخدم لرسم المتجة في الفضاء وتحديد نقطة البداية والنهاية.

ax = plt.axes()
ax.arrow(0.0, 0.0, A[0], A[1], head_width=0.4, head_length=0.5)
plt.annotate(f"A({A[0]},{A[1]})", xy=(A[0], A[1]),xytext=(A[0]+0.5, A[1]))
ax.arrow(0.0, 0.0, B[0], B[1], head_width=0.4, head_length=0.5)
plt.annotate(f"B({B[0]},{B[1]})", xy=(B[0], B[1]),xytext=(B[0]+0.5, B[1]))

4. في هذه الخطوة يتمّ رسم المحاور (X) و(Y)، ويكون الناتجُ النهائيّ للمخطط الرّسميّ للمتّجهَين كما في الشّكل(2)

plt.xlim(0,10)
plt.ylim(0,10)
plt.show()
plt.close()

5.حسابُ قيمة جيب التّمام كما في المعادلة أعلاه في المتغير(cos_sim)

cos_sim=np.dot(A,B)/(np.linalg.norm(A)*np.linalg.norm(B))
print (f"Cosine Similarity between A and B:{cos_sim}")

وتكون النّتيجة كما في التالي:

Cosine Similarity between A and B:0.7241379310344827

الشّكل(2) يوضح مخطّط الرّسم للمتّجهَين (A)و(B) باستخدام مكتبة الرسم البياني في بايثون

تطبيقٌ عمليّ على بيانات نصيّة Implementation

لتطبيق حساب تشابه-جيب التّمام على البيانات النصية، تستخدم الدوال المبنيّة داخليّاً (Inbuilt Function) في مكتبة اس-كي للتعلم، والتي تقوم بحساب  تشابه-جيب التّمام عن طريق استخدام المعادلة(1) الموضحة سابقاً أوالتي يتمّ تمثيلها مباشرةً عند استخدام الدالّة ( cosine_similarity).

تطبيقٌ عمليّ 

والآن عزيزي القارئ في هذا المثال سوف نستخدم ثلاث مستنداتٍ نصيّة (DQ,DA,DB)، يمثل (DQ) الاستعلام(query) الذي نبحث عن وجود متشابهٍ له في الدّيوان النّصيّ (corpus)، وفي هذا التطبيق يتكون الدّيوان النّصيّ من مستندَين يتمّ تمثيلها من خلال (DA,DB).

1.الدّيوان النصيّ

DQ="البرمجة بلغة بايثون"
DA="تستخدم البرمجة بلغة بايثون في معالجة اللغات الطبيعية" 
DB="مقدمة في استخدام بايثون"

2.وضع المستندات في شكلِ مصفوفةٍ من الكلمات

documents = [DQ,DA,DB]

3.نحتاج إلى استيراد كلٍّ من مكتبة اس-كي-للتعلّم(sklearn)ومكتبة تحليل البيانات في بايثون (بانداس)

from sklearn.feature_extraction.text import CountVectorizer
import pandas as pd

4.نقوم بتحويل المستندات إلى متّجهات رقميّة من خلال الصّنف (CountVectorizer)، ونضعها في مصفوفةٍ مستخدمين الدالّة (fit_transform)

count_vectorizer = CountVectorizer()
sparse_matrix = count_vectorizer.fit_transform(documents)

5.يتمّ تحويل المصفوفة من الكلمات إلی شكل عرضٍ توضيحيّ، نستطيع من خلاله رؤيةَ الكلمات وعددَ مرّات ظهور كلّ كلمة في كل مستند على حِدى  مستخدمين الداّة (DataFrame) من المكتبة بانداس، وتكون المصفوفةُ كما في الشّكل(3)

doc_term_matrix = sparse_matrix.todense()
df = pd.DataFrame(doc_term_matrix, 
                  columns=count_vectorizer.get_feature_names(), 
                  index=['DQ', 'DA', 'DB'])

الشّكل(3)عدد مرّات ظهور كلّ كلمةٍ في كلّ مستند

6.استخدام دالّة تشابه-جيب التّمام الموجودة في مكتبة اس-كي-للتعلّم لحساب نسبة التشابه بين المستندات الموجودة، وتظهر النّتيجة كما في الشّكل(4) والذي يوضّح أنّ نسبة التشابه بين المستندَين (DQ,DB) هي الأكبر قيمة والأكثر تطابقاً بنسبةٍ تصل إلى(0.61237244)، بالإضافة إلى ذلك يجب أن نلاحظ أنّ قطر المصفوفة هو تشابه-جيب التّمام لكلّ مستندٍ مع نفسه، لذلك تكون النتيجةُ 1 والتى تمّ تمثيلها بالدّوائر الحمراء في الشّكل(4) وهي دلالةٌ على التّطابق التام.

import pprint
from sklearn.metrics.pairwise import cosine_similarity
pprint.pprint(cosine_similarity(sparse_matrix))

الشّكل(4)القيم المختلفة لتشابه-جيب التّمام لكلّ المستندات

التردد العكسي Inverted Index

إن التردد العكسي هو مصطلح يستخدم لبناء هيكل بيانات مفهرسة تستخدم لتخزين الخرائط من محتوى معين,علي سبيل المثال لا الحصر مواقع الكلمات والارقام في مستند أو مستندات معينة.وبكلمات بسيطة ان التردد العكسي هو عبارة عن بناء قاموس يحتوي علي كل الكلمات في كل المستندات المعنية, مع تحديد رقم المستند الذي يحتوي على كل كلمة.ويعتبر التردد العكسي من أكثر الطرق المستخدمة فعالية وسرعة عند استخدامه في عمليات البحث.

سوف نوضح في هذا الجزء كيفية بناء التردد العكسي من مجموعة من المستندات وذلك باستخدام ملف يحتوي علي 3 اسطر سوف نعتبر كل سطر هو عبارة عن مستند وبذلك يكون لدينا ثلاثة مستندات سوف نستخدمها لبناء التردد العكسي كما في الخطوات التالية:

1. سوف نقوم بإنشاء ملف البيانات كما في الشفرة البرمجية التالية:

%%writefile Data.txt
We propose a matching algorithm 
the data for the retrieval process
Java programming language

2.فتح الملف للقراءة كما في الشفرة البرمجية التالية:

file = open('file.txt', encoding='utf8')
read = file.read()
file.seek(0)
read

3.قراءة وتحديد عدد السطور في الملف المعين

line = 1
for word in read:
    if word == '\n':
        line += 1
print("Number of lines in file is: ", line)

4.عمل مصفوفة بالمستندات وتخزين كل مستند كعنصر منفصل في هذه المصفوفة

array = []
for i in range(line):
    array.append(file.readline())
array

5.عملية التقسيم إلى وحدات لغوية ولمعرفة المزيد من التفاصيل عن هذه الطريقة يمكنك عزيزي القارئ مراجعة هذا المقال.

from nltk.tokenize import word_tokenize
for i in range(1):
     text_tokens = word_tokenize(read)

6.وفي هذة الخطوة سوف نقوم بازالة كلمات الوقف من المستندات ولمعرفة المزيد من التفاصيل عن هذة الطريقة يمكنك عزيزي القارئ الرجوع الي هذا المقال.

from nltk.corpus import stopwords
nltk.download('stopwords')
tokens_without_sw = [
    word for word in text_tokens if not word in stopwords.words()]
print(tokens_without_sw)

وتكون المخرجات كما في الشكل (5)

الشكل (5) توضيح الكلمات في شكل منفصل بعد استخراجها من المستندات وازالة كلمات الوقف

7.في هذه الخطوة الأخيرة يتم بناء التردد العكسي باستخدام طريقة بناء القاموس في بايثون ,وتكون المخرجات عبارة عن كل الكلمات الموجودة في المستندات الثلاث وبعد ازالة كلمات الربط يتبقى لدينا تسعة كلمات تتكون منها المستندات الثلاث كما موضح في الشكل (6).

dict = {}
for i in range(line):
    check = array[i].lower()
    for item in tokens_without_sw:
          if item in check:
            if item not in dict:
                dict[item] = []
  
            if item in dict:
                dict[item].append(i+1)
 dict

{'algorithm': [1],
 'data': [2],
 'language': [3],
 'matching': [1],
 'process': [2],
 'programming': [3],
 'propose': [1],
 'retrieval': [2]}

الشكل (6) توضيح التردد العكسي للمستندات

عزيزي القارئ يمكنك الاطلاع على كامل الشفرة البرمجية code في مستودع المدونة على الغيت هب

الخاتمة Conclusion

تعدّ خوارزميّة تشابه-جيب التّمام من أفضل الخوارزميّات المستخدمة في محرّكات البحث، ولذلك  تنتشرُ انتشاراً واسعاً لدى مطّوري النظم ومحلّلي البيانات في مختلف المجالات، ومهما كانت حجمُ البيانات فإنّ من أهمّ مميّزات هذه الخوارزميّة هي السّرعة والكفاءة العالية في الحصول على أفضل النّتائج.وعلى صعيد تحسين عمليات البحث وجعلها اكثر سرعة واكثر فعالية عندما تكون البيانات ضخمة يمكن استخدام طريقة بناء التردد العكسي الموضحة من خلال هذا المقال .

وبعد أن تعرفنا سوياً عزيزي القارئ على خوارزميّة تشابه-جيب التّمام، وطريقة عملها على البيانات الرقميّة والنصيّة في تطبيقاتٍ عمليّة واضحة ومفهومة، سوف نستمر في تقديمِ شروحاتٍ مفصّلة للعديد من الخوارزميّات التي تُستخدم في معالجة اللّغات الطبيعيّة (NLP).

المراجع References

1. https://towardsdatascience.com/cosine-similarity-how-does-it-measure-the-similarity-maths-behind-and-usage-in-python-50ad30aad7db
2. https://www.machinelearningplus.com/nlp/cosine-similarity/
3. Jbara, K., 2010. Knowledge discovery in Al-Hadith using text classification algorithm. Journal of American Science, 6(11), pp.409-19.
4. https://www.geeksforgeeks.org/create-inverted-index-for-file-using-python/
5. Büttcher, S., Clarke, C.L. and Cormack, G.V., 2016. Information retrieval: Implementing and evaluating search engines. Mit Press.
6. https://aiinarabic.com/glossary/