استخدام شبكات الطيّ العصبونيّة CNN في نقل النّمط وتصميم الصّور – إنشاء تأثيرات جميلة للصّور

تخيل أنك تستطيع مزج صورة لسماء مدينة بوسطن الأمريكيّة (الصّورة في اليسار)، مع لوحة فنيّة للرّسّام العالميّ المشهور فان كوخ (الصّورة في الوسط)،  ونتج عن ذلك صورة جديدة لسماء مدينة بوسطن ولكن بالنّمط الفنيّ لصورة فان كوخ (الصّورة على اليمين). تُسمّى هذه العملية بنقل النمط العصبوني.

سنقوم في هذا المقال بإنشاء تأثيرات نقل نمط style transfer مميّزة، وللقيام بذلك يتوجّب علينا فهم كيفيّة عمل شبكات الطّيّ العصبونيّة وطبقاتها بشكل أعمق. بعد الانتهاء من قراءة هذا المقال ستتمكن _عزيزي القارئ _ من إنشاء تطبيقات نقل نمط قادرة على تطبيق نمطٍ جديد على الصّورة، مع الحفاظ على محتواها الأصليّ كما في مثال صورة سماء مدينة بوسطن المذكور أعلاه والموضّح في الشكل (1).

نقل النّمط

دعونا في البداية نوضّح ما نسعى لتحقيقه في تطبيقات نقل النّمط.

لنقم بتعريف نقل النّمط كعمليّة تعديل لنمط صورةٍ ما مع الحفاظ على محتواها، وبالتالي في حال كان لدينا صورة ما (صورة الدّخل) وصورة أخرى (صورة النّمط)، فيمكننا حساب صورة الخرج والتي هي عبارة عن محتوى صورة الدّخل ولكن بنمطٍ جديد، و قد تمّت الإشارة إلى هذه العمليّة في الورقة البحثيّة للباحث ليون أ. غاتيس Leon A.Gatys [1].

صورة الدّخل + صورة النّمط –> صورة خرج (صورة الدّخل بنمط صورة النّمط)

كيف يعمل نقل النّمط؟

1. نأخذ صورة الدّخل وصور النّمط ونُغيّر أحجامها لتكون متساوية. 
2. نقوم بتحميل شبكة طيّ عصبونيّة مدرّبة مسبقًا، ولتكن على سبيل المثال شَبَكَةُ مجموعةِ الهندسةِ البصريَّة  في جي جي (VGG16) 
3. بمعرفتنا أنّه يمكننا تمييز الطّبقات الأولى المسؤولة عن النّمط (الأشكال الأساسيّة، الألوان، …) عن الطبقات المسؤولة عن المحتوى (المزايا الخاصّة بالصّورة)، نقوم بفصل تلك الطّبقات من أجل أن نستطيع العمل على كلٍّ من النّمط والمحتوى بشكلٍ مستقلّ.
4. أصبحت الآن مسألتنا هي مسألة تحسين حيث ستكون مهمّتنا تصغير ما يلي:

• خسارة المحتوى (المسافة بين صور الدّخل والخرج – حيث نسعى جاهدين للحفاظ على المحتوى).
• خسارة النّمط (المسافة بين صور النّمط وصور الخرج – حيث نسعى جاهدين لتطبيق نمطٍ جديد).
• خسارة الاختلاف الكليّ (التّنظيم – التّنعيم على مستوى البكسل لتقليل ضجيج صورة الخرج).

 الخطوة الأخيرة هي ضبط المشتقات gradients وتحسينها عن طريق استخدام خوارزميّة برويدن-فليتشر-غولدفراب-شانو محدودة الذاكرة Limited-Memory Broyden–Fletcher–Goldfarb–Shanno algorithm (L-BFGS). يمكنكم ملاحظة أنّ الخوارزميّة أخذت اسمها من أسماء العلماء الأربعة الذين قاموا بإيجادها.

خوارزميّة ب-ف-غ-ش محدودة الذاكرة L-BFGS

تمّ إنشاء هذه الخوارزميّة من قبل خورخي نوسيدال Jorge Nocedal، في مركز التّحسين كمشروعٍ مشترك بين مختبر أرغون الوطنيّ  Argonne National Laboratory وجامعة نورث ويسترن Northwestern، كُتبت شيفرة المصدر بلغة البرمجة فورتران FORTRAN ويُشار إليها على أنّها خوارزميّة تحسين غير محدود ذي  نطاق واسع، تعتبر هذه الخوارزميّة من عائلة خوارزمية ب-ف-غ-ش BFGS، ولكنّها تمتاز أنها تَستخدم ذاكرة أقلّ، لهذا تُعتبر مثاليّة من أجل مجموعات البيانات الكبيرة.

التّطبيق العمليّ

يمكنك -عزيزي القارئ- إيجاد الشّيفرة البرمجيّة لمشروع نقل النّمط العصبونيّ على مستودع الشّيفرة البرمجيّة الخاصّ بموقع الذّكاء الاصطناعيّ باللّغة العربيّة هنـــا.

المُعاملات الأساسيّة

فيما يلي نبيّن قيم المُعاملات الأساسيّة التي سيتمّ استخدامها في الشّيفرة البرمجيّة لاحقاً، وهي على  التّرتيب: عدد دورات  التّدريب، عدد قنوات الصّور، عرض وارتفاع الصّور، مصفوفة المتوسّط الحسابيّ لبكسلات كلّ من قنوات الألوان الأحمر R والأخضر G والأزرق B لكلّ صور قاعدة بيانات إيمج-نت، أوزان المحتوى و النّمط، وأخيراً وزن الاختلاف الكليّ.

ITERATIONS = 10
CHANNELS = 3
IMAGE_SIZE = 500
IMAGE_WIDTH = IMAGE_SIZE
IMAGE_HEIGHT = IMAGE_SIZE
IMAGENET_MEAN_RGB_VALUES = [123.68, 116.779, 103.939]
CONTENT_WEIGHT = 0.02
STYLE_WEIGHT = 4.5
TOTAL_VARIATION_WEIGHT = 0.995

الدّخل

في البداية، دعونا نُعرّف صورة الدّخل وهي صورة لسماء مدينة سان فرانسيسكو  كما هو مبيّن في الشّكل (2). تتمّ قراءة صورة الدّخل باستخدام مكتبة بيل PIL من مسار محدّد، بعد ذلك نقوم بتغيير حجمها إلى حجم محدّد مسبقاً كما هو مُبيّن في  الشّيفرة  البرمجيّة  التّالية:

input_image_path = "input.png"
san_francisco_image_path = r'images/' + input_image_path
input_image = Image.open(san_francisco_image_path)
input_image = input_image.resize((IMAGE_WIDTH, IMAGE_HEIGHT))
input_image

النّمط

بعد ذلك، دعونا نُعرّف صورة النّمط وهي لوحة فنيّة لتيتوس بروزوزوسكي Tytus Brzozowski يُعبّر فيها عن رؤيته لمدينة وارسو في بولّندا كما هو مبيّن في الشّكل (3).

style_image_path = "style.png"
tytus_image_path = r'images/' + style_image_path
style_image = Image.open(tytus_image_path)
style_image = style_image.resize((IMAGE_WIDTH, IMAGE_HEIGHT))
style_image

تحضير البيانات

خطوتنا التّالية هي إجراء عمليّة تغيير أبعاد Reshape وتقييس Normalization لصور الدّخل والنّمط، حيث تمّ تحويل تمثيل الصّور من التّرميز اللّونيّ  أحمر-أخضر-أزرق RGB إلى  التّرميز أزرق-أخضر-أحمر BGR  RGB إلى BGR كما تمّ تقييس مصفوفات الصّور، عن طريق طرح قيمة المتوسّط الحسابيّ من كل قناة من قنوات الصّور،  ويتمّ الحصول على مصفوفة المتوسّط الحسابيّ – مصفوفة ثلاثيّة الأبعاد – عن طريق حساب المتوسّط الحسابيّ لبكسلات كلّ من قنوات الألوان الأحمر R والأخضر G والأزرق B لكلّ صور قاعدة بيانات إيمج-نت، تمّ في هذا التّطبيق العمليّ إعطاء قيم مصفوفة المتوسّط الحسابيّ في المتحوّل IMAGENET_MEAN_RGB_VALUES.

input_image_array = np.asarray(input_image, dtype="float32")
input_image_array = np.expand_dims(input_image_array, axis=0)
input_image_array[:, :, :, 0] -= IMAGENET_MEAN_RGB_VALUES[2]
input_image_array[:, :, :, 1] -= IMAGENET_MEAN_RGB_VALUES[1]
input_image_array[:, :, :, 2] -= IMAGENET_MEAN_RGB_VALUES[0]
input_image_array = input_image_array[:, :, :, ::-1]
style_image_array = np.asarray(style_image, dtype="float32")
style_image_array = np.expand_dims(style_image_array, axis=0)
style_image_array[:, :, :, 0] -= IMAGENET_MEAN_RGB_VALUES[2]
style_image_array[:, :, :, 1] -= IMAGENET_MEAN_RGB_VALUES[1]
style_image_array[:, :, :, 2] -= IMAGENET_MEAN_RGB_VALUES[0]
style_image_array = style_image_array[:, :, :, ::-1]

نموذج شبكة الطيّ العصبونيّة CNN

بعد قيامنا بتطبيق عمليّة التقييس وحصولنا على مصفوفات الصّور، يمكننا تعريف نموذج الطّيّ العصبونيّ، حيث سنقوم في هذا المشروع باستخدام نموذج في جي جي 16 (VGG16) المُدرّب مسبقًا، والذي له البنية الموضّحة في الشّكل (4)

input_image = backend.variable(input_image_array)
style_image = backend.variable(style_image_array)
combination_image = backend.placeholder((1, IMAGE_HEIGHT, IMAGE_SIZE, 3))
input_tensor = backend.concatenate([input_image,style_image,combination_image], axis=0)
model = VGG16(input_tensor=input_tensor, include_top=False)

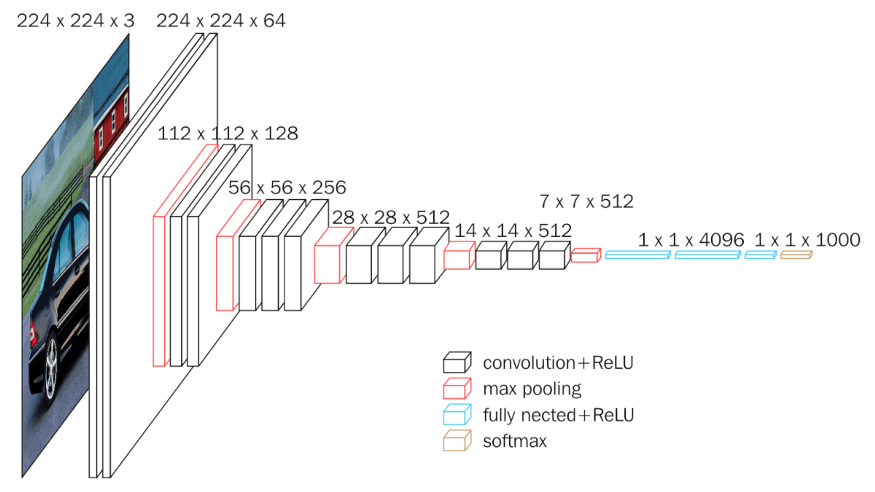
يُرجى الانتباه أنّنا لن نستخدم الطّبقة ذات الاتصال الكامل (اللّون الأزرق) و طبقة سوفت ماكس (اللّون الأصفر) و اللّتان تُعتبران طبقات تصنيف لا نحتاجها في هذا المشروع، فنحن نهتمّ بالطّبقات التي تعمل كمُستخرجات مزايا؛ أي طبقات الطّيّ (اللّون الأسود) و طبقات التّجميع وفق القيمة الكبرى (اللّون الأحمر).

 يبيّن الشّكل (5) كيف تبدو بعض المزايا عند طبقات محدّدة في نموذج في جي جي ،16 المُدرّب على مجموعة بيانات إيمج-نت ImageNet.

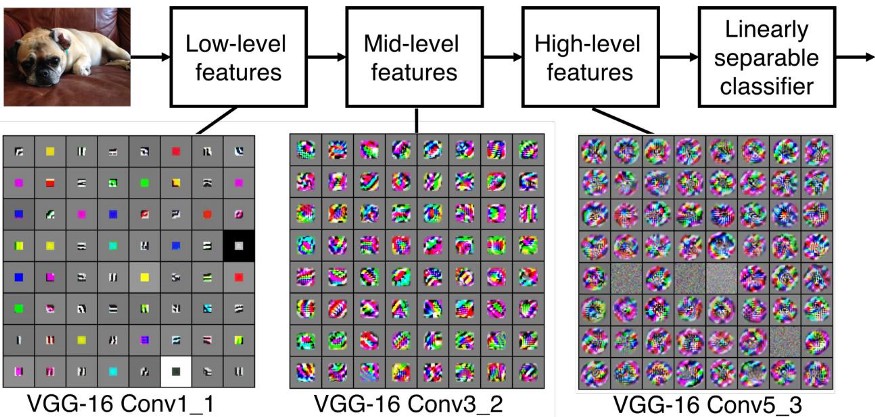
لن نقوم بعرض مزايا كلّ طبقة طيّ في النّموذج ولكن حسب جونسن Johnson et al. [2] يمكن اختيار الطّبقة ذات الاسم block2_conv2 كطبقة محتوى والطّبقات التّالية كطبقات النّمط.

[block1_conv2, block2_conv2, block3_conv3, block4_conv3, block5_conv3]

ملاحظة: لقد تمّ إثبات أنّ هذه المجموعة من الطّبقات تعمل بشكل جيد، ولكن لا ضير من تجريب  طبقات أخرى .

خسارة المحتوى

نّ خطوتنا التّالية بعد تعريف نموذج شبكة الطّيّ العصبونيّة، هي تعريف دالة خسارة المحتوى، فمن أجل الحفاظ على المحتوى الأصليّ لصورة الدّخل، سنقوم بتقليل المسافة بين صورة الدّخل وصورة الخرج. تُبيّن الأسطر  البرمجيّة  التّالية  كيفيّة حساب خسارة المحتوى، التي يلزمنا من أجل حسابها تحديد كلٍ من مزايا المحتوى ومزايا مصفوفة الدّمج (دمج مصفوفتي المحتوى و النّمط). كما رأينا سابقاً، يُمكننا اعتبار الطّبقة ذات الاسم block2_conv2 كطبقة محتوى، و بالتّالي يمكن إيجاد مزايا المحتوى بالاستفادة من هذه  الطّبقة التي تمّ تمثيلها بتينسور رباعيّ له  الشّكل  (3,250,250,128) والذي تمّ إنشاؤه من ثلاث مصفوفات (مصفوفة الدّخل في الموقع 0، مصفوفة  النّمط في الموقع 1 ومصفوفة الدّمج في الموقع 2)، كلّ مصفوفة منها لها الحجم  التّالي (250,250,128). الآن أصبح من  السّهل تحديد مصفوفتي مزايا الدّخل والدّمج  اللّتان لهما المواقع التّالية  0 و 2 على التّرتيب  باستخدام طريقة التّشريح Slicing.

أخيراً تمّ حساب الخسارة عن طريق استدعاء دالّة الخسارة، التي ستقوم بحساب مجموع مربّعات الفروقات بين بكسلات مصفوفة المحتوى و مصفوفة الدّمج.

def content_loss(content, combination):
return backend.sum(backend.square(combination - content))

layers = dict([(layer.name, layer.output) for layer in model.layers])

content_layer = "block2_conv2"
layer_features = layers[content_layer]
content_image_features = layer_features[0, :, :, :]
combination_features = layer_features[2, :, :, :]

loss = backend.variable(0.)
loss += CONTENT_WEIGHT * content_loss(content_image_features, combination_features)

خسارة النّمط

يتمّ تعريف خسارة النّمط أيضًا على أنّها المسافة بين صورتين بشكلٍ مشابهٍ لخسارة المحتوى، ولكن هذه المرّة المسافة ستكون بين صورة النّمط وصورة الخرج. تمّ تحديد مزايا النّمط ومزايا الدّمج بنفس الطّريقة السّابقة، عن طريق الاستفادة من الطّبقات التي تُخزّن مزايا النّمط كما رأينا سابقاً. ولكن هنا تمّت مقارنة مصفوفات الجرام Gram Matrices لمصفوفات النّمط والدّمج بدلاً من مقارنة قيم تلك المصفوفات بشكلٍ مباشر. يمكنكم الاطّلاع على مصفوفة الجرام وكيفية حسابها عن طريق الاطّلاع على المقالة التّالية “نقل النّمط العصبونيّ: إنشاء عملٍ فنيٍّ بالتّعلم العميق باستخدام كيراس tf.keras و منفّذ إيجر eager” المنشورة على موقع الذّكاء الاصطناعيّ باللّغة العربيّة.

def gram_matrix(x):
features = backend.batch_flatten(backend.permute_dimensions(x, (2, 0, 1)))

gram = backend.dot(features, backend.transpose(features))
return gram

def compute_style_loss(style, combination):
style = gram_matrix(style)
combination = gram_matrix(combination)
size = IMAGE_HEIGHT * IMAGE_WIDTH
return backend.sum(backend.square(style - combination)) / (4. * (CHANNELS ** 2) * (size ** 2))

style_layers = ["block1_conv2", "block2_conv2", "block3_conv3", "block4_conv3", "block5_conv3"]

for layer_name in style_layers:
layer_features = layers[layer_name]

style_features = layer_features[1, :, :, :]
combination_features = layer_features[2, :, :, :]
style_loss = compute_style_loss(style_features, combination_features)

loss += (STYLE_WEIGHT / len(style_layers)) * style_loss

خسارة الاختلاف الكليّ

أخيرًا سنقوم بتعريف الخسارة الكليّة والتي ستعمل كمُنعّم مكانيّ على مستوى البكسل من أجل منع الضّجيج في صورة الخرج.

def total_variation_loss(x):
a = backend.square(x[:, :IMAGE_HEIGHT-1, :IMAGE_WIDTH-1, :] - x[:, 1:, :IMAGE_WIDTH-1, :])
b = backend.square(x[:, :IMAGE_HEIGHT-1, :IMAGE_WIDTH-1, :] - x[:, :IMAGE_HEIGHT-1, 1:, :])
return backend.sum(backend.pow(a + b, TOTAL_VARIATION_LOSS_FACTOR))

loss += TOTAL_VARIATION_WEIGHT * total_variation_loss(combination_image)

التّحسين- الخسارة والمُشتقّات

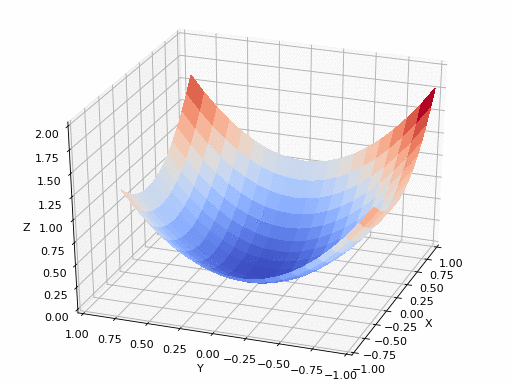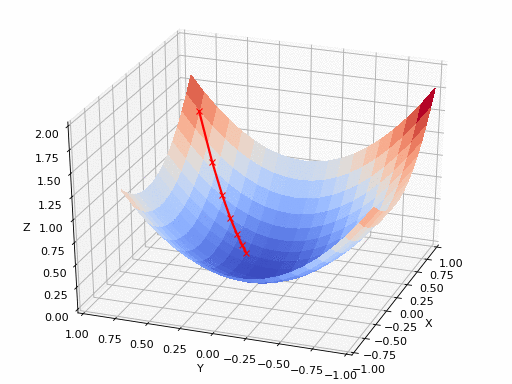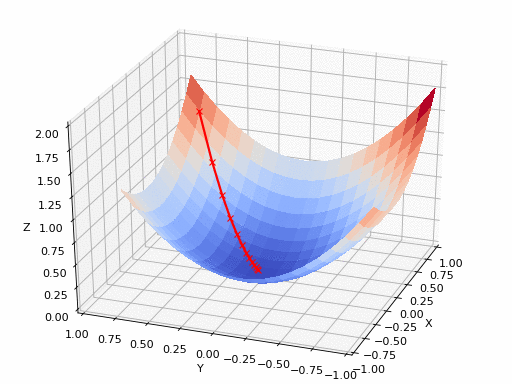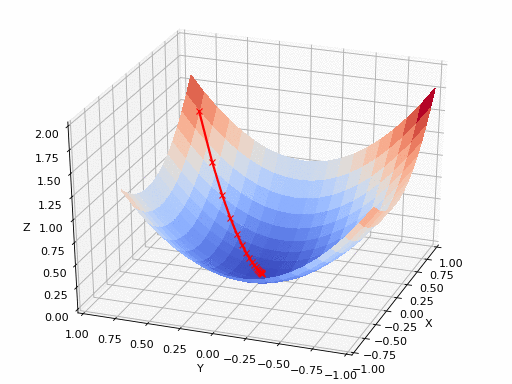
الآن بعد أن قمنا بتعريف خسارة المحتوى وخسارة النّمط والخسارة الكليّة، يمكننا تعريف عمليّة نقل النّمط العصبونيّ على أنّها مهمّة تحسين سيتمّ من خلالها تقليل الخسارة النّهائيّة (وهي مزيج من خسائر المحتوى والنّمط والاختلاف الكليّة) عن طريق تطبيق خوارزمية انحدر المُشتق Gradient Descent التي يبين الشكل (6) رسماً توضيحياً لآلية عملها.

دعونا نفكّر في عمليّة نقل النّمط على الشّكل التّالي: في كلّ دورة تدريب، سنقوم بإنشاء صورةِ خرج بحيث يتمّ تقليل المسافة بين الخرج وصور الدّخل والنّمط في طبقات المزايا الموافقة لكلٍّ من صورة الدّخل وصورة النّمط.

outputs = [loss]
outputs += backend.gradients(loss, combination_image)

def evaluate_loss_and_gradients(x):
x = x.reshape((1, IMAGE_HEIGHT, IMAGE_WIDTH, CHANNELS))
outs = backend.function([combination_image], outputs)([x])
loss = outs[0]
gradients = outs[1].flatten().astype("float64")
return loss, gradients

class Evaluator:
def loss(self, x):
loss, gradients = evaluate_loss_and_gradients(x)
self._gradients = gradients
return loss

def gradients(self, x):
return self._gradients

evaluator = Evaluator()

النّتائج

تمّ استخدام خوارزميّة التّحسين ب-ف-غ-ش محدودة الذاكرة L-BFGS،  و إنّ الشّيفرة البرمجيّة التّالية تبيّن عمليّة التّحسين وتقوم بعرض صورة الخرج في دورات التّدريب التّالية (1، 2، 5، 10) كما هو واضح في الشّكل (7).

x = np.random.uniform(0, 255, (1, IMAGE_HEIGHT, IMAGE_WIDTH, 3)) - 128.

for i in range(ITERATIONS):
x, loss, info = fmin_l_bfgs_b(evaluator.loss, x.flatten(), fprime=evaluator.gradients, maxfun=20)
print("Iteration %d completed with loss %d" % (i, loss))

x = x.reshape((IMAGE_HEIGHT, IMAGE_WIDTH, CHANNELS))

x = x[:, :, ::-1]
x[:, :, 0] += IMAGENET_MEAN_RGB_VALUES[2]
x[:, :, 1] += IMAGENET_MEAN_RGB_VALUES[1]
x[:, :, 2] += IMAGENET_MEAN_RGB_VALUES[0]
x = np.clip(x, 0, 255).astype("uint8")

output_image = Image.fromarray(x)
output_image.save(output_image_path)
output_image

الآن دعونا نرى في الشّكل (8) كيف ستبدو صور الدّخل والنّمط والخرج مجتمعة.

هذا يبدو مثيراً للإعجاب أليس كذلك؟

يمكننا بوضوح أن نلاحظ أنّه بينما تمّ الحفاظ على المحتوى الأصلي للصورة المُدخلة (أفق مدينة سان فرانسيسكو)، تمكنّا بنجاح من تطبيق نمطٍ جديدٍ  (لوحة مدينة وارسو لتيتوس برزوزوسكي) على صورة الخرج.

أمثلة أخرى

يبين الشّكل (9) مجموعة من الصّور التي تمّ تعديل نمطها عن طريق إضافة أنماط لأعمال فنيّة مختلفة.

والآن ماذا بعد ذلك؟

لقد أثبتنا إمكانيّة الاستفادة من شبكات الطّيّ العصبونيّة CNN وطبقاتها، التي تعمل كمُستخرجات للمزايا لإنشاء تأثيرات نقل نمط رائعة، أشجعك عزيزي القارئ أن تقوم بتغيير المُعاملات الأساسيّة Hyperparameters وأن تغيّر إعدادات طبقات الشّبكة العصبونيّة من أجل تحقيق نتائج أفضل، لا تتردّد في مشاركة نتائجك.

وأخيراً لا تنسَ أن تلقي نظرة على الشّيفرة البرمجيّة للمشروع على جيت هب هنـــا.

المراجع

1.  A Neural Algorithm of Artistic Style
2. Perceptual Losses for Real-Time Style Transfer and Super-Resolution
3. style-transfer-styling-images-with-convolutional-neural-network
4. neural-style-transfer-creating-art-with-deep-learning