سنتعلم في هذه المقالة كيفية توظيف التعلم العميق في تشكيل صور باستخدام نمط صورة أخرى أو ما يدعى بنقل النمط العصبوني وقد قام بشرح هذه التقنية ليون أ.جاتيس Leon A. Gatys في ورقته المسماة الخوارزمية العصبونية للأسلوب الفني وهي تعتبر ورقة رائعة يمكن الرجوع لها أيضًا للتعمق في فهم هذه التقنية. نقل النمط العصبوني هو تقنية تحسين تقوم بأخذ ثلاث صور وهي صورة المحتوى وصورة مرجعية للنمط (مثل عمل فني لرسام مشهور) وصورة الدخل التي نريد تطبيق النمط عليها ومن ثم مزجهم معًا لتصبح العملية وكأننا نحوّل صورة الدخل لتبدو كصورة المحتوى لكن مرسومة في نمط صورة النمط.
على سبيل المثال لنأخذ صورة سلحفاة البحر الأخضر المرسومة من قبل بير ليندغرين وصورة الموجة الكبيرة في كاناغاوا التي تم رسمها من قبل هوكوساي
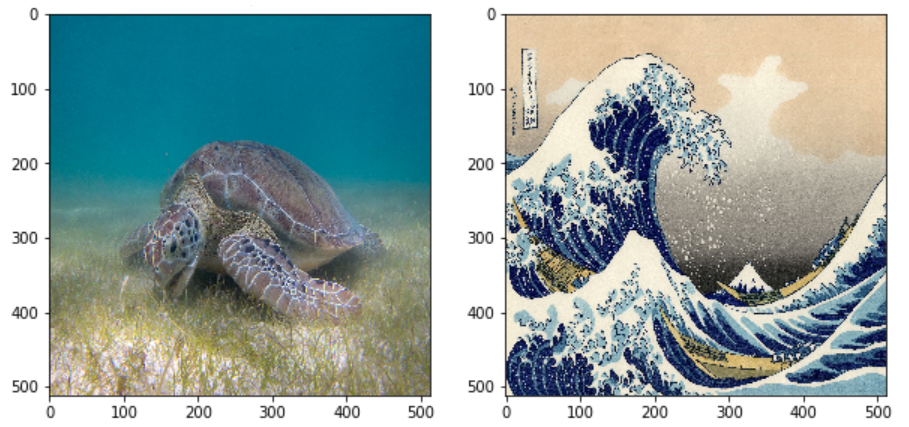
على فرض قرر هوكوساي إضافة نسيج أو نمط موجاته إلى صورة لسلحفاة ؟كيف سيكون الأمر؟ النتيجة ستكون كما في الشكل(2)

يعتبر نقل النمط تقنية رائعة تُظهر قدرات الشبكات العصبونية و تمثيلها الداخلي. ويعتمد مبدأ هذه التقنية على تحديد تابعي مسافة الأول لوصف اختلاف المحتوى بين صورتين يدعى Lcontent والآخر يصف اختلاف نمطي الصورتين ويدعى Lstyle. تقوم هذه العملية بتعديل نمط صورة الدخل مع الحفاظ على محتواها بعدة خطوات:
1- أخذ كل من صورة الدخل والنمط وجعل حجمها متساوي
2- تحميل شبكة الطيّ العصبونية المسماة مجموعة الهندسة البصرية VGG16
مع العلم أنه يمكننا التمييز بين الطبقات المسؤولة عن النمط (الأشكال الأساسية والألوان وما إلى ذلك) والطبقات المسؤولة عن المحتوى (مزايا الصورة الخاصة) ويمكن فصلهم للعمل بشكل مستقل على المحتوى والنمط
3- ثم تحديد المهمة كمشكلة تحسين حيث سنقوم بتقليل خسارة المحتوى (المسافة بين صورة الدخل والخرج والمحاولة قدر الإمكان المحافظة على المحتوى) وتقليل خسارة النمط (المسافة بين صورة النمط ونمط صورة الخرج والمحاولة قدر الإمكان لتطبيق نمط جديد) وذلك من خلال تطبيق الانتشار العكسي.
4- وأخيرًأ تعيين المشتق والقيام بالتحسين باستخدام محسن آدم.
بعض المفاهيم التي سيتم التطرق لها
– منفّذ إيجر Eager Execution: تستخدمه البيئة البرمجية الأساسية لتنسرفلو TensorFlow لتقييم العمليات بشكل فوري.من أجل تعلم المزيد عن منفذ إيجر يمكنكم الاطلاع على الرابط التالي منفذ إيجر
2– استخدام واجهة برمجة التطبيقات الوظيفية في كيراس في بناء النموذج: سنقوم باستخدام واجهة برمجة التطبيقات كيراس لتعريف نموذجنا من أجل الوصول إلى الطبقات المتوسطة المقابلة لخرائط مزايا النمط والمحتوى.
3- الاستفادة من خرائط المزايا لنموذج مدرب مسبقًا : سنتعلم كيفية استخدام النماذج المدربة مسبقًأ مع خرائط مزاياها.
4- إنشاء حلقات تدريب مخصصة: سنقوم بفحص كيفية ضبط المحسّن لتقليل الخسارة مع أخذ معاملات الدخل بعين الاعتبار.
خطوات نقل النمط العصبوني
ستتم مرحلة نقل النمط من خلال الخطوات التالية:
- رسم الصور المدخلة
- المعالجة الأساسية (تحضير البيانات)
- ضبط توابع الخسارة
- إنشاء النموذج
- تحسين تابع الخسارة
هذه المقالة موجهة لأصحاب الخبرة المتوسطة بمفاهيم تعلم الآلة و لفهم المقالة بشكل جيد يجب قراءة ورقة جاتيس ويجب وجود معرفة سابقة عن انحدار المشتق gradient descent.
يمكن تحميل الشيفرة البرمجية الكاملة لهذه المقالة من الجيت هوب . كما يمكن تتبع الخطوات مع الشرح من هنا.
مرحلة التنفيذ
سنبدأ بتفعيل منفذ إيجر الذي سيسمح لنا العمل خلال هذه التقنية في أوضح وأبسط طريقة.
tf.enable_eager_execution()
print("Eager execution: {}".format(tf.executing_eagerly()))
# Set up some global values here
content_path = '/tmp/nst/Green_Sea_Turtle_grazing_seagrass.jpg'
style_path = '/tmp/nst/The_Great_Wave_off_Kanagawa.jpg'
plt.figure(figsize=(10,10))
content = load_img(content_path).astype('uint8')
style = load_img(style_path).astype('uint8')
plt.subplot(1, 2, 1)
imshow(content, 'Content Image')
plt.subplot(1, 2, 2)
imshow(style, 'Style Image')
plt.show()
تنفيذ الشيفرة السابقة سيعطي رسم لصورتي المحتوى والنمط كما في الشكل (1).
1- تحديد المحتوى وتمثيلات النمط
تُمثل الطبقات القليلة الأولى ابتداء من طبقة الدخل المزايا قليلة المستوى مثل الحواف والملمس بينما تمثل الطبقات الأخيرة المزايا عالية المستوى لاجزاء الغرض مثل العجلات أو العيون، أمّا الطبقات المتوسطة في الشبكة المدربة مسبقًا لتصنيف الصور VGG19 فهي تعتبر الضرورية لتحديد تمثيلات المحتوى والنمط من الصور. ومن خلال أخذ صورة الدخل ومطابقة تمثيلات المحتوى والنمط على هذه الطبقات سنحصل على صورة الخرج المطلوبة.
لماذا الطبقات المتوسطة؟
ربما تتساءلون لماذا خرج الطبقات المتوسطة في شبكة التصنيف المدربة مسبقًا تسمح لنا في تحديد تمثيلات النمط والمحتوى. يمكن تفسير ذلك على أنه لكي تستطيع الشبكة القيام بتصنيف الصور يجب عليها فهم الصورة وذلك من خلال أخذ الصورة كبكسلات دخل وبناء التمثيلات الداخلية من خلال التحويلات التي تحول هذه البيكسلات إلى فهم معقد للمزايا الموجودة داخل الصورة. هذا أيضًا يعتبر السبب في أن شبكات الطيّ العصبونية قادرة على التعميم الجيد فهي قادرة على التقاط الثوابت وتحديد المزايا داخل الأصناف( قطط، كلاب،….) والتي لا تتعلق بضجيج الخلفية وغيرها من الإزعاجات لذلك في مكان ما حيث يتم إدخال الصورة وإعطاء تسمية الصنف كخرج يعمل النموذج كمستخرج للمزايا المعقدة. وبالتالي من خلال الوصول إلى الطبقات المتوسطة يمكننا وصف المحتوى ونمط الصورة المدخلة. لذلك سنقوم الآن بسحب هذه الطبقات المتوسطة من شبكتنا.
# Content layer where will pull our feature maps
content_layers = ['block5_conv2']
# Style layer we are interested in
style_layers = ['block1_conv1',
'block2_conv1',
'block3_conv1',
'block4_conv1',
'block5_conv1'
]
num_content_layers = len(content_layers)
num_style_layers = len(style_layers)
2- بناء النموذج
عملية البناء ستتم بكتابة التابع ()get_model الذي سيقوم بتحميل نموذج تصنيف الصور المدرب مسبقًا (مجموعة الهندسة البصرية) VGG19 على مجموعة بيانات إيمج نت ImageNet ومن ثم استخدام واجهة برمجة التطبيقات كيراس للوصول إلى الطبقات المتوسطة المقابلة لخرائط ميزات النمط والمحتوى لدينا لاستخدامها في بناء نموذجنا الجديد بالتالي استخراج خرائط المزايا للمحتوى والنمط والصور التي تم إنشاؤها. ونظرًا لكون VGG19 نموذجًأ بسيطًا بالمقارنة مع شبكة الرواسب ResNet وإينسبشن Inception فإن خرائط المزايا تعمل بشكل أفضل في نقل النمط.
def get_model():
vgg = tf.keras.applications.vgg19.VGG19(include_top=False, weights='imagenet')
vgg.trainable = False
# Get output layers corresponding to style and content layers
style_outputs = [vgg.get_layer(name).output for name in style_layers]
content_outputs = [vgg.get_layer(name).output for name in content_layers]
model_outputs = style_outputs + content_outputs
# Build model
return models.Model(vgg.input, model_outputs)
ستعيد الشيفرة البرمجية السابقة النموذج ذو الدخل المحدد بالصورة والخرج المحدد بالطبقات المتوسطة لصورة المحتوى والنمط .
3- تحديد وإنشاء توابع الخسارة (تابعي المسافة) لكلا من المحتوى والنمط
أولاً: خسارة المحتوى.
إن تعريف خسارة المحتوى بسيط للغاية حيث سنقوم بتمرير كلا من صورة المحتوى مع صورة الدخل الأساسية للشبكة ليعيد خرج الطبقات المتوسطة من نموذجنا.ثم ببساطة سنأخذ المسافة الإقليدية بين التمثيليين المتوسطين لتلك الصور.
أي أن خسارة المحتوى هي عبارة عن تابع يصف مسافة المحتوى من صورة الدخل x و صورة المحتوى p.
- على فرض أن Cₙₙ هي شبكة الطيّ العصبونية المدربة مسبقًأ وهنا أيضًا سنستخدم VGG19.
- على فرض أن X هي أي صورة عندها ستكون(Cₙₙ(x هي الشبكة التي تُغذا بالصورة X.
- وكذلك كلا من (Fˡᵢⱼ(x)∈ Cₙₙ(x و (Pˡᵢⱼ(x) ∈ Cₙₙ(x يصفان تمثيل المزايا المتوسطة للشبكة مع الدخل x و p في الطبقة i.
بهذا يمكن وصف تابع مسافة المحتوى على الشكل التالي.
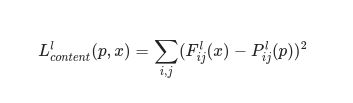
قمنا بتطبيق الانتشار العكسي لتقليل خسارة المحتوى حيث يتم في كل مرة تغيير صورة التهيئة إلى حين الحصول على استجابة مماثلة في طبقة معينة وهي الطبقة المحددة بطيقة المحتوى كما في صورة المحتوى الأساسية سيتم تنفيذ التابع بسرعة وسيكون دخله خرائط المزايا في الطبقة L في الشبكة التي دخلها صورة الدخل x وصورة المحتوى p وسيعيد مسافة المحتوى.
def get_content_loss(base_content, target):
return tf.reduce_mean(tf.square(base_content - target))
ثانياً: خسارة النمط
سيتم حساب خسارة النمط بنفس المبدأ لكن هنا سيكون دخل الشبكة صورة الدخل الأساسية مع صورة النمط و بدلًا من مقارنة خرج الطبقات المتوسطة للصورة الأساسية وصورة النمط ستقارن مصفوفات الجرام Gram matrices لكلا الخرجين.
قبل شرح الشكل الرياضي سنوضح بعض المصطلحات وذلك لتسهيل الفهم:
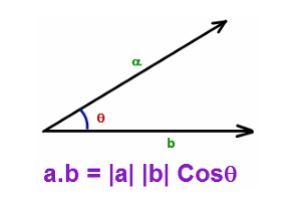
1– الجداء الداخلي (الجداء النقطي): يعبر عن الجداء النقطي لشعاعين بالشكل (3) ,هو عبارة عن مجموع ناتج جداء احداثياتها الخاصة أو يمكن القول أنه يعبر عن مدى تشابه شعاعين وكلما كان هذان الشعاعين أكثر تشابهًا كلما قلت الزاوية و كلما تشابهوا كلما زاد ناتج الجداء النقطي.

– مصفوفة الجرام:
على فرض لدينا شعاعين من المزايا المسطحة يمثلان مزايا الدخل من خريطة المزايا ذات العمق C، الجداء النقطي لهم في هذه الحالة سيعطينا العلاقة بينهم. فكلما كان ناتج الجداء أقل كل ما كانت المزايا المكتسبة أكثر اختلافًأ وبالعكس كل ما الناتج أكبر كل ما كانت المزايا أكثر ارتباطًا بمعنى آخر كلما كان الجداء أقل كلما قل تضافر المزايا وكلما كان أكبر كلما زاد حدوثهما معًا . بهذا نكون عرفنا معلومات حول نمط الصورة.
ومن خلال المرور على كل شعاع ميزة (سطر) من خريطة المزايا ذات العمق C وحساب الجداء النقطي له مع نفسه ومع بقية الأشعة الأخرى سيكون الناتج مصفوفة الجرام ذات الحجم CxC والمعبر عنها بالعلاقة.
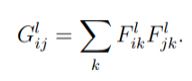
– استجابات المرشح: .يمكن فهم كل طبقة من طبقات شبكات الطيّ العصبونية على أنها مجموعة من المرشحات والتي يقوم كل منها باستخراج مزايا محددة من صورة الدخل بالتالي خرج الطبقة سيكون مجموعة من ما يسمى خرائط المزايا.
استخدمت مصفوفة الجرام لتمثيل نمط الصورة وهي تعبر عن العلاقة بين استجابات المرشح المختلفة (المزايا) التي تعكس معلومات مختلفة عن البنية. الطبقة ذات Nl مرشح مختلف لها Nl خريطة مزايا.
اذًا ولحساب خسارة النمط بالشكل رياضي سيتم وصف خسارة النمط لصورة الدخل الأساسي x وصورة النمط a كمسافة بين تمثيل النمط (مصفوفات الجرام) لهذه الصور. نحن نصف تمثيل النمط للصورة كعلاقة بين استجابات المرشح المختلفة المعطاة بمصفوفة الجرام Gˡ بينما Gˡᵢⱼ هو الجداء الداخلي بين خريطة المزايا الموجهة i و j في الطبقة I.
نستطيع أن نرى بأن Gˡᵢⱼ التي تم إنشاؤها على خريطة المزايا للصورة المعطاة تمثل العلاقة بين خرائط المزايا i و j.
لإنشاء النمط لصورة الدخل الأساسية سنقوم بإجراء انحدار المشتق من صورة المحتوى لتحويله إلى صورة تتطابق مع تمثيل النمط للصورة الأصلية. سنقوم بذلك من خلال تقليل متوسط المسافة المربعة بين خريطة علاقة المزايا لصورة النمط والدخل. مساهمة كل طبقة في خسارة النمط الكلي تصف بالشكل:
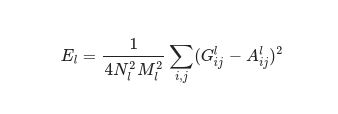
حيث أن Gˡᵢⱼ و Aˡᵢⱼ يعبران عن تمثيلات النمط في الطبقة I من صورة الدخل x وصورة النمط a و Nl تصف عدد خرائط المزايا كل منها بحجم Ml والذي يساوي جداء الارتفاع مضروبًا بعرض خريطة المزايا. بالتالي خسارة النمط الكلية عبر كل الطبقات هو:
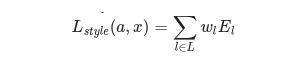
بينما مساهمة كل طبقة تتعلق ببعض العوامل ونقيسها بالعلاقة التالية:
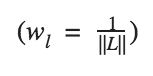
و الشيفرة البرمجية المقابلة لما سبق بالشكل التالي:
def gram_matrix(input_tensor):
# We make the image channels first
channels = int(input_tensor.shape[-1])
a = tf.reshape(input_tensor, [-1, channels])
n = tf.shape(a)[0]
gram = tf.matmul(a, a, transpose_a=True)
return gram / tf.cast(n, tf.float32)
def get_style_loss(base_style, gram_target):
"""Expects two images of dimension h, w, c"""
# height, width, num filters of each layer
# We scale the loss at a given layer by the size of the feature map and the number of filters
height, width, channels = base_style.get_shape().as_list()
gram_style = gram_matrix(base_style)
return tf.reduce_mean(tf.square(gram_style - gram_target))# / (4. * (channels ** 2) * (width * height) ** 2)
4- تفعيل انحدار المشتق Gradient Descent
في حال لم يكن هناك معلومات كافية عن انحدار المشتق أو الانتشار العكسي أو في حال الرغبة بمراجعة بعض المعلومات عنهم يمكن مراجعة الرابط .
سنقوم باستخدام محسنّ آدم Adam لإنقاص الخسارة. وسنقوم بالتحديث المتكرر لصورة الخرج بالشكل الذي يقلل من الخسارة. لا نقوم بتحديث الأوزان المرتبطة بشبكتنا لكن بدلًا من ذلك ندرب صورة الدخل لإنقاص الخسارة وللقيام بذلك يجب أن نعرف كيفية حساب الخسارة وانحدار المشتق. كان من الممكن استخدام المحسنّ L-BFGS لكن في هذه المقالة كان الدافع الأساسي توضيح أفضل تطبيق لمنفذ إيجر ومع استخدام محسنّ آدم نستطيع شرح وظيفة شريط لانحدار مع حلقات تدريب خاصة.
حساب الخسارة والانحدار.
سنقوم بتعريف تابع مساعد بسيط ليقوم بتحميل صورة المحتوى والنمط ومن ثم إدخالهم بالانتشار الأمامي لشبكتنا لتعطي الخرج والذي يمثل تمثيلات المزايا لكلا من النمط والمحتوى من نموذجنا.
def get_feature_representations(model, content_path, style_path):
# Load our images in
content_image = load_and_process_img(content_path)
style_image = load_and_process_img(style_path)
# batch compute content and style features
style_outputs = model(style_image)
content_outputs = model(content_image)
# Get the style and content feature representations from our model
style_features = [style_layer[0] for style_layer in style_outputs[:num_style_layers]]
content_features = [content_layer[0] for content_layer in content_outputs[num_style_layers:]]
return style_features, content_features
هنا سنستخدم الواجهة التي توفرها تنسرفلو tf.GradientTape من أجل حساب الاشتقاق الآلي حيث تقوم تنسرفلو بتسجيل جميع العمليات التي تنفذ ضمن tf.GradientTape خلال عملية الانتشار الأمامي على شريط “tape”. ثم تستخدم Tensorflow هذا الشريط والانحدارات المرتبطة بكل عملية مسجلة لحساب الانحدارات لتوابع الخسارة مع مراعاة صورة الدخل في عملية الانتشار الخلفي.
سنقوم الآن ببناء التابع compute_loss ليقوم بحساب الخسارة الكلية وسنمرر له عدة معاملات وهي:
1- النموذج model: الذي من خلاله سنصل إلى الطبقات المتوسطة.
2- أوزان الخسارة loss_weights: أوزان جميع توابع الخسارة (وزن النمط، وزن المحتوى. ووزن الاختلاف الكلي).
3- صورة التهيئة init_image: صورتنا الأساسية وهي ما سنقوم بتحديثه أثناء عملية التحسين. سنقوم بحساب الانحدارات مع الأخذ بعين الاعتبار الخسارات التي سنقوم بحسابها لهذه الصورة
صورة التهيئة و هي ناتج عملية التحسين
4- مصفوفة الجرام لمزايا النمط gram_style_features: مصفوفات الجرام التي تم حسابها سابقًا والمطابقة لطبقات النمط المحددة.
5- مزايا المحتوى content_features: الخرج المحسوب مسبقًا من طبقات المحتوى المحددة.
ليعيد الخسارة الكلية وخسارة النمط وخسارة المحتوى.
def compute_loss(model, loss_weights, init_image, gram_style_features, content_features):
style_weight, content_weight, total_variation_weight = loss_weights
نقوم بتمرير صورة التهيئة للنموذج ليعطينا بدوره تمثيلات النمط والمحتوى في الطبقات المرغوبة وباعتبار أننا نستخدم إيجر سيتم استدعاء هذا النموذج كأي تابع آخر
model_outputs = model(init_image)
style_output_features = model_outputs[:num_style_layers]
content_output_features = model_outputs[num_style_layers:]
style_score = 0
content_score = 0
وبعدها حساب تراكم خسارات النمط من جميع الطبقات وهنا يتم حساب الوزن عند كل طبقة داخلة في حساب الخسارة
weight_per_style_layer = 1.0 / float(num_style_layers)
for target_style, comb_style in zip(gram_style_features, style_output_features):
style_score += weight_per_style_layer * get_style_loss(comb_style[0], target_style)
تراكم خسارات المحتوى من جميع الطبقات
weight_per_content_layer = 1.0 / float(num_content_layers)
for target_content, comb_content in zip(content_features, content_output_features):
content_score += weight_per_content_layer* get_content_loss(comb_content[0], target_content)
style_score *= style_weight
content_score *= content_weight
حساب الخسارة الكلية
loss = style_score + content_score
return loss, style_score, content_score
والشيفرة البرمجية للتابع compute_loss بشكل كامل:
def compute_loss(model, loss_weights, init_image, gram_style_features, content_features):
style_weight, content_weight = loss_weights
model_outputs = model(init_image)
style_output_features = model_outputs[:num_style_layers]
content_output_features = model_outputs[num_style_layers:]
style_score = 0
content_score = 0
weight_per_style_layer = 1.0 / float(num_style_layers)
for target_style, comb_style in zip(gram_style_features, style_output_features):
style_score += weight_per_style_layer * get_style_loss(comb_style[0], target_style)
weight_per_content_layer = 1.0 / float(num_content_layers)
for target_content, comb_content in zip(content_features, content_output_features):
content_score += weight_per_content_layer* get_content_loss(comb_content[0], target_content)
style_score *= style_weight
content_score *= content_weight
loss = style_score + content_score
return loss, style_score, content_score
وبهذا أصبح حساب الانحدار بسيط من خلال تعريف التابع compute_grads.
def compute_grads(cfg):
with tf.GradientTape() as tape:
all_loss = compute_loss(**cfg)
total_loss = all_loss[0]
return tape.gradient(total_loss, cfg['init_image']), all_loss
5- تطبيق وتشغيل عملية نقل النمط
سيتم ذلك من خلال كتابة التابع run_style_transfer وسنمرر له عدة معاملات وهي مسار كل من صورة المحتوى content_path وصورة النمط style_path وعدد مرات التكرار سنحددها ب1000 وأخيرًأ وزن خسارة المحتوى بقيمة افتراضية 1000 و وزن خسارة النمط بقيمة افتراضية 0.01 بهذا الضبط لمعاملات الوزن يمكن تحقيق التوازن بين صورة المحتوى والنمط بالتالي تقليل الضجيج في الصورة الناتجة.
لسنا بحاجة أو لا نريد تدريب أي من طبقات النموذج لذلك سنبدأ بضبط خاصية قابلية التدريب من أجل جميع الطبقات إلى القيمة False.
import IPython.display
def run_style_transfer(content_path,
style_path,
num_iterations=1000,
content_weight=1e3,
style_weight=1e-2):
model = get_model()
for layer in model.layers:
layer.trainable = False
ثم سنقوم بعملية الحصول على تمثيلات مزايا المحتوى والنمط من الطبقات المتوسطة المحددة
style_features, content_features = get_feature_representations(model, content_path, style_path)
gram_style_features = [gram_matrix(style_feature) for style_feature in style_features]
بعدها سيتم ضبط صورة التهيئة وفي البداية ستكون نفسها صورة المحتوى ونطيق عملية التحسين باستخدام محسنّ آدم لتقليل الخسارات.
init_image = load_and_process_img(content_path)
init_image = tf.Variable(init_image, dtype=tf.float32)
opt = tf.train.AdamOptimizer(learning_rate=5, beta1=0.99, epsilon=1e-1)
وبعدها سنقوم بتعريف متحولات لتخزين أفضل قيمة للخسارة وأفضل صورة كنتيجة وضبط مصفوفة معاملات التابع compute_grads التي ذكرناها سابقًا (ذاتها الخاصة بالتابع compute_loss)وذلك لتمريرها عند استدعائه.
iter_count = 1
best_loss, best_img = float('inf'), None
loss_weights = (style_weight, content_weight)
cfg = {
'model': model,
'loss_weights': loss_weights,
'init_image': init_image,
'gram_style_features': gram_style_features,
'content_features': content_features
}
الخطوات الاخيرة تتضمن العرض مع عملية التحديث في كل تكرار لكل من الخسارة (اختيار أفضل خسارة من مجمل الخسارات) مع الصورة (افضل صورة ذات خسارة كلية أقل) مع تحويل صورة الدخل من الصيغة المحملة بها إلى صيغة مكتبة بايثون العددية Numpy ليعيد التابع بالنهاية أقل خسارة وأفضل صورة.
num_rows = 2
num_cols = 5
display_interval = num_iterations/(num_rows*num_cols)
start_time = time.time()
global_start = time.time()
norm_means = np.array([103.939, 116.779, 123.68])
min_vals = -norm_means
max_vals = 255 - norm_means
imgs = []
for i in range(num_iterations):
grads, all_loss = compute_grads(cfg)
loss, style_score, content_score = all_loss
opt.apply_gradients([(grads, init_image)])
clipped = tf.clip_by_value(init_image, min_vals, max_vals)
init_image.assign(clipped)
end_time = time.time()
if loss < best_loss:
best_loss = loss
best_img = deprocess_img(init_image.numpy())
if i % display_interval== 0:
start_time = time.time()
plot_img = init_image.numpy()
plot_img = deprocess_img(plot_img)
imgs.append(plot_img)
IPython.display.clear_output(wait=True)
IPython.display.display_png(Image.fromarray(plot_img))
print('Iteration: {}'.format(i))
print('Total loss: {:.4e}, '
'style loss: {:.4e}, '
'content loss: {:.4e}, '
'time: {:.4f}s'.format(loss, style_score, content_score, time.time() - start_time))
print('Total time: {:.4f}s'.format(time.time() - global_start))
IPython.display.clear_output(wait=True)
plt.figure(figsize=(14,4))
for i,img in enumerate(imgs):
plt.subplot(num_rows,num_cols,i+1)
plt.imshow(img)
plt.xticks([])
plt.yticks([])
return best_img, best_loss
والشيفرة البرمجية للتابع run_style_transfer بشكل كامل:
import IPython.display
def run_style_transfer(content_path,
style_path,
num_iterations=1000,
content_weight=1e3,
style_weight=1e-2):
model = get_model()
for layer in model.layers:
layer.trainable = False
style_features, content_features = get_feature_representations(model, content_path, style_path)
gram_style_features = [gram_matrix(style_feature) for style_feature in style_features]
init_image = load_and_process_img(content_path)
init_image = tf.Variable(init_image, dtype=tf.float32)
opt = tf.train.AdamOptimizer(learning_rate=5, beta1=0.99, epsilon=1e-1)
iter_count = 1
best_loss, best_img = float('inf'), None
loss_weights = (style_weight, content_weight)
cfg = {
'model': model,
'loss_weights': loss_weights,
'init_image': init_image,
'gram_style_features': gram_style_features,
'content_features': content_features
}
num_rows = 2
num_cols = 5
display_interval = num_iterations/(num_rows*num_cols)
start_time = time.time()
global_start = time.time()
norm_means = np.array([103.939, 116.779, 123.68])
min_vals = -norm_means
max_vals = 255 - norm_means
imgs = []
for i in range(num_iterations):
grads, all_loss = compute_grads(cfg)
loss, style_score, content_score = all_loss
opt.apply_gradients([(grads, init_image)])
clipped = tf.clip_by_value(init_image, min_vals, max_vals)
init_image.assign(clipped)
end_time = time.time()
if loss < best_loss:
best_loss = loss
best_img = deprocess_img(init_image.numpy())
if i % display_interval== 0:
start_time = time.time()
plot_img = init_image.numpy()
plot_img = deprocess_img(plot_img)
imgs.append(plot_img)
IPython.display.clear_output(wait=True)
IPython.display.display_png(Image.fromarray(plot_img))
print('Iteration: {}'.format(i))
print('Total loss: {:.4e}, '
'style loss: {:.4e}, '
'content loss: {:.4e}, '
'time: {:.4f}s'.format(loss, style_score, content_score, time.time() - start_time))
print('Total time: {:.4f}s'.format(time.time() - global_start))
IPython.display.clear_output(wait=True)
plt.figure(figsize=(14,4))
for i,img in enumerate(imgs):
plt.subplot(num_rows,num_cols,i+1)
plt.imshow(img)
plt.xticks([])
plt.yticks([])
return best_img, best_loss
سنقوم بآخر خطوة بعملية الاستدعاء للتابع على صورتا السلحفاة والموجة الكبرى لهوكوساي:
best, best_loss = run_style_transfer(content_path,
style_path, num_iterations=1000)
النتيجة النهائية لتنفيذ الشيفرة البرمجية بشكل كامل في مراحل تكرار مختلفة ستكون على الشكل التالي:



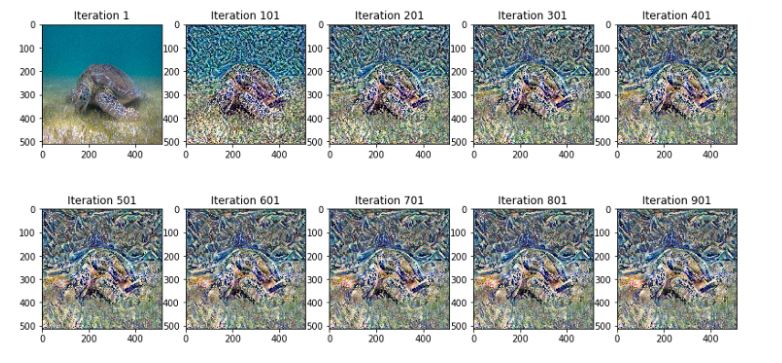
يمكن التجريب على صور أخرى مختلفة وهذه بعض الأمثلة:
1- صورة لمدينة توبينغن الألمانية من قبل أندرياس بريفكي مع صورة لليلة النجوم بواسطة فنسنت فان جوخ.
2- صورة لمدينة توبينغن الألمانية من قبل أندرياس بريفكي مع صورة التكوين 7 بواسطة فاسيلي كاندينسكي
3- صورة لمدينة توبينغن الألمانية من قبل أندرياس بريفكي مع .صورة أركان الابداع من قبل وكالة ناسا وفريق هابل للتراث.
يمكن تجريب أي صور أخرى.
الخاتمة
قمنا في هذه المقالة بتطبيق تقنية النقل العصبوني لتحويل صورة الدخل لتبدو كصورة المحتوى لكن مرسومة في نمط صورة النمط وذلك باستخدام كيراس مع منفّذ إيجر وقمنا بضبط توابع الخسارة باستخدام الانتشار العكسي لتقليل الخسارات. والعمل كان بعدة خطوات حيث بدأنا بتحميل نموذج مدرب مسبقا واستخدمنا خرائط المزايا المدربة له لوصف المحتوى وتمثيل النمط للصور. يحسب تابع الخسارة بشكل أساسي المسافة بين تعابير هذه التمثيلات المختلفة. ثم نفذنا ذلك على نموذج مخصص بنيناه باستخدام واجهة برمجة التطبيقات مع منفذ إيجر الذي سمح لنا بالعمل الديناميكي مع المصفوفة متعددة الأبعاد باستخدام تدفق تحكم بايثون الطبيعي.
أخيراً حدثنا صورتنا بشكل متكرر من خلال تطبيق قواعد المحسنّ باستخدام tf.gradient وقد قام المحسنّ بتقليل الخسارة المعطاة مع الأخذ بعين الاعتبار صورة الدخل.





