هل فكرتَ يوماً بمعرفة الإجابة الصحيحة لألعاب المنطق باستخدام الرؤية الحاسوبيّة، ألم تفكر يوماً بأنّك ربّما تقوم بحلّ ألعاب المنطق بشكل خاطئ؟
أو كيف لك معرفة الإجابة الصحيحة أو المكان الذي قد أخطأت به؟
إنّ ألعاب المنطق تأخذ الكثيرَ من الجهد والوقت لمعرفة الإجابة النّهائيّة والتي ربّما قد تكون خاطئة، تابع المقالة لمعرفة أشهر 3 ألعاب (سودوكو، ستار باتل، سكايسكرايبر) بالإضافة لمعرفة الإجابة الصّحيحة بأجزاء من الثّانية فقط.
كيفيّة حلّ ألعاب المنطق باستخدام الرؤية الحاسوبيّة والذّكاء الاصطناعيّ
سنستخدم أدوات بايثون لحلّ ألعاب المنطق في الزّمن الحقيقيّ (مثل سودوكو sudoku) باستخدام مكتبة الرؤية الحاسوبيّة مفتوحة المصدر OpenCV، وخوارزميّات التّراجع backtracking algorithm والقليل من التّعلّم العميق Deep Learning.

نتيجة للتّوجه الحاليّ إلى الرؤية الحاسوبيّة وخوارزميات الذّكاء الصنعيّ، والاهتمام الكبير بألعاب المنطق، كان لابدّ من توظيف تقانات الذّكاء لحلّ ألعاب المنطق، لذلك قمنا ببناء برنامجٍ يقوم بدمجهم معاً، برنامج يقوم بعمليّة الاكتشاف والتّحليل كما يقوم بحلّ بعض ألغاز المنطق مثل السّودوكو والسّكايسكرايبر Skyscrapers.
سنقدّم لكم في هذا المقال شرحاً لحلّ ألعاب المنطق. يحتوي الموضوع علی ثلاثة مجالاتٍ للدّراسة:
- الرؤية الحاسوبيّة لاكتشاف الألغاز في الصّورة المدخلة.
- التعلّم العميق لتصنيف أيّ رقم في اللّغز.
- الذّكاء الاصطناعيّ لحلّ اللّعبة.
البرنامج مكتوب بلغة البايثون باستخدام OpenCV وتنسور فلو tensorflow وهو قادر على حلّ ثلاثة أنواعٍ من الألعاب : سودوكو، ستار باتل star Battle، سكايسكرايبر.
1- لعبة السّودوكو: تتكون لعبة السّودوكو من تسعة أعمدةٍ طوليّة، وتسعة صفوفٍ أفقية، وتسع مناطق صغيرة، ويطلق على الواحدة منها خليّة، بحيث يصبح المجموع النّهائي واحداً وثمانين خليّة مقسمةً على الأعمدة والصفوف التسعة، وتوضع الأرقام في الخلايا الفارغة وتُرتّب من واحد إلى تسعة.
قواعد اللعبة: يجب أن يستخدم الرّقم مرةً واحدة لا غير في كلّ سطر، وكلّ صف، وكلّ رقعة فرعيّة، وبشكلٍ عام تحتوي لعبة السّودوكو على سبعة عشر رقماً فارغاً على الأقل، وفي أنماط أخرى أكثر صعوبةً قد يتراوح العدد من 22 إلى 30 مربعاً فارغاً.
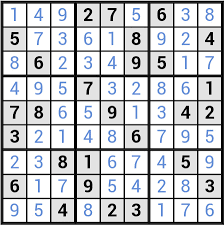
2- لعبة ستار باتل: تتكوّن لعبة ستار باتل من رقعةٍ مربّعة، الهدف منها استخدام المنطق لتحديدِ مكان النّجوم في رقعة اللّعب المتوفرة.
قواعد اللّعبة: ظهورعددٍ معين من النّجوم في كلّ صفٍّ وعمود ومنطقة، لايمكن أن يكون هناك نجمان متجاوران، ولا حتى بشكلٍ مائل. من هذا الافتراض البسيط يأتي لغز معقّد، حيث أنه في الأمثلة الأكبر يجب وضع نجمتين في كلّ منطقة، في حين أنّ المثال الصغير يحتوي على نجمةٍ واحدة فقط لكلّ منطقة (يحتوي كلّ صفٍ وعمود ومنطقة على نفس عددِ النجوم، نجمةٍ واحدة للمستوى الأول مثلاً أو نجمتين للمستوى الثاني وهكذا).

3- لعبة سكايسكرايبر: تتكون لعبة سكايسكرايبر من أربعة أعمدةٍ طولية وأربعة صفوفٍ أفقية، فكر في رقعة اللعبة على أنها مدينة مليئة بناطحاتِ السحاب المختلفة. الهدف من اللعبة هو ملء اللوحة بأبراجٍ ذات ارتفاعاتٍ مختلفة، لذلك سميت سكايسكرايبر: أي ناطحات سحاب
قواعدُ اللعبة: نظرًا لأنها لعبة 4×4، فستحتاج إلى بناء أربعة أبراج مكوّنة من أربع كتل وأربعة أبراج مكوّنة من ثلاث كتل وأربعة أبراج مكوّنة من مبنيين وأربعة أبراج أحادية الكتلة، يمكنك صنع هذه الأبراج باستخدام الألوان لترميزها بحيث يكون لكلّ ارتفاع لونه الخاصّ لملء الرّقعة، يمكنك استخدام القواعد النموذجيّة من سودوكو أي يجب أن يحتوي كل صف وكل عمود على جميع الارتفاعات الأربعة.

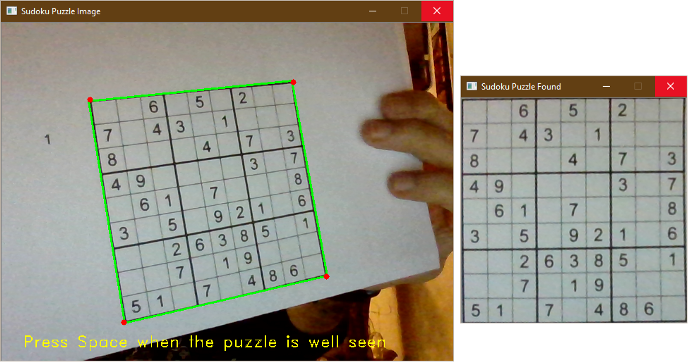
الخطوة الأولى: اكتشاف اللّغز:
تتمثّل الخطوة الأولى باكتشاف اللّغز في الصّورة المدخلة.
الفكرة هي العثور على أكبر محيط في الصّورة بمعنى آخر أكبر مضلّع، ولتصبح هذه الخطوة هي أسهل للبرنامج يفضّل بأن يكون المشهد واضحاً، مع أقلّ قدرٍ ممكن من الضّوضاء والأشياء التي قد تؤدّي إلى سوء فهم عناصرالصّورة.
def findPolygon(self, img):
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
blurred = cv2.GaussianBlur(gray, (7, 7), 3)
thresh = cv2.adaptiveThreshold(blurred, 255,cv2.ADAPTIVE_THRESH_GAUSSIAN_C, cv2.THRESH_BINARY, 11, 2)
thresh = cv2.bitwise_not(thresh, thresh)
cnts = cv2.findContours(thresh.copy(), cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)[0]
contours = sorted(cnts, key=cv2.contourArea, reverse=True)
polygon = contours[0]
return polygon
تمّ إيجاد المحيط باستخدام التّابع findCountours وذلك باستخدام المعامل cv2.RETR_EXTERNAL للنّظر فقط في المحيط الخارجيّ، ثم نقوم بفرز الخطوط العريضة حسب مساحتها ونأخذ العنصر الأوّل.
src_polygon = np.array([top_left, top_right, bottom_right, bottom_left], dtype='float32')
dst_polygon = np.array([[0, 0], [size - 1, 0], [size - 1, size - 1], [0, size - 1]],dtype='float32')
m = cv2.getPerspectiveTransform(src_polygon, dst_polygon)
img = cv2.warpPerspective(img, m, (int(size), int(size)))
بمجرّد معرفة نوع اللّغز، نأخذ الرّؤوس الأربعة لحساب تحويل المنظور وتشويه صورة المضلّع باستخدام WarpPerspective
قبل المتابعة يجب علينا استخراج صور الخلايا (أي استخراج الارقام الموجودة في المربعات) من رقعة اللّعبة لتحليل الأرقام المكتوبة فيها.
squares = []
grid_len = self.game_info['GRID_LEN'] # Ex. 9
side = img.shape[:1][0] / (grid_len)
for j in range(grid_len):
for i in range(grid_len):
p1 = (int(i * side), int(j * side))
p2 = (int((i + 1) * side), int((j + 1) * side))
squares.append((p1, p2))
digits = []
for idx, square in enumerate(squares):
square_roi = img[square[0][1]:square[1][1], square[0][0]:square[1][0]]
extracted_digit = self.get_digit(square_roi)
if extracted_digit is not None:
digits.append(extracted_digit)
لاحظ أنّ طول رقعة اللعبة مُعطی من قِبل المستخدم. يحلّل التّابع get_digit صورة الخليّة للتّحقق ممّا إذا كانت تحتوي على رقم (وإلّا فلن تُرجع شيئاً) ثمّ يقوم بمعالجتها لجعلها متناسبةً مع دخل مصنّف الأرقام.
الخطوة الثّانية: تحليل اللّغز
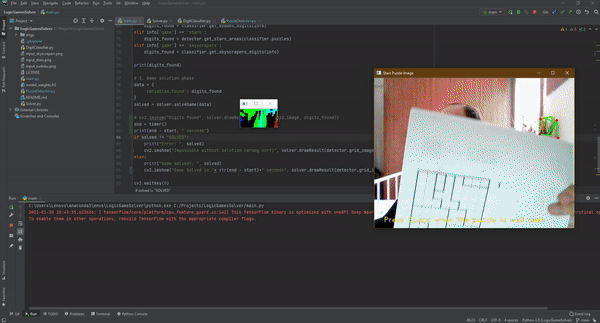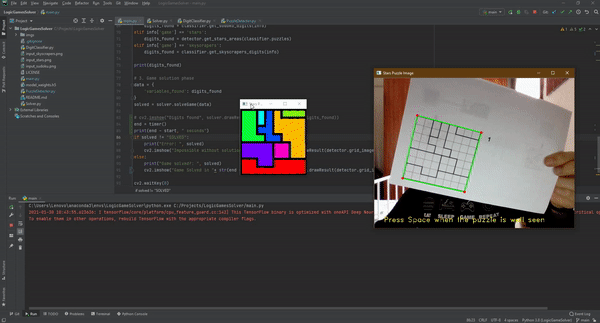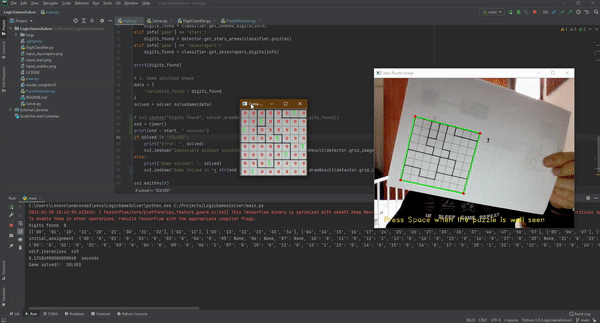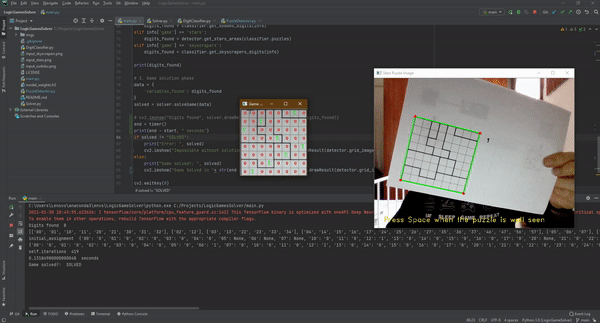
بمجرّد أن نحصل على الصّورة المستوية للغز، نبدأ بتحليل الصّورة للحصول على المعلومات المقدّمة مسبقاً لحلّ اللّعبة.
هناك بعض الأرقام التي يجب أن تُؤخذ بعين الاعتبار لكلٍّ من لغزي السّودوكو والسّكايسكرايبر، أمّا لعبة ستار باتل نحتاج لفهم الهيكل الدّاخليّ لتحدي المناطق الموجودة في المخطّط.
مصنّف الأرقام
لفهم ما هي الأرقام الموجودة في اللّغز، يستفيد النّظام من شبكة الطيّ العصبونيّة المصمّمة للأرقام المكتوبة بخطّ اليد، والتي تمّ تصنيفها وتدريبها بواسطة مجموعة البيانات الشّهيرة إم نيست
MNIST dataset²: 60,000 تتألف من 60000 عينة كلّ عينة عبارة عن صورةٍ مربّعة صغيرة بأبعاد 28×28 بالتّدرج الرّماديّ، تشكل العينات أرقام مُفردة مكتوبة بخطّ اليد بين 0 و9
لا نريد التّحدث عن مصنّف الأرقام بشكل مفصّل كونه من أساسيّات CNN، أما dataset فيمكن معرفة المزيد عنه من خلال متابعة مقالاتنا على المدوّنة، أما الآن فسنتابع فقط الهندسة البنائيّة للشّبكة العصبونية.
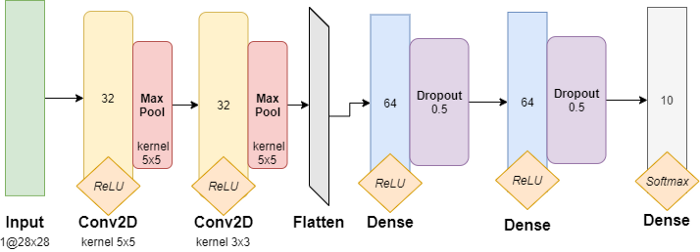
نلاحظ في الشكل (7) بنية CNN المستخدمة كما تحدّثنا فإنّ الدّخل عبارة عن صورة ذات الأبعاد 28×28 وهي رمادية، كما يحتوي النموذج على طبقتي طيّ مطبّق عليهم تابع التفعيل وحدة التصحيح الخطي Relu Rectified Linear Unit، وتجميع وفق القيمة الكبرى max pooling وطبقة تسطيح flatten وطبقتين كاملتي الاتصال Dense، كلّ طبقة تحوي 64 عصبون مطبّق عليهم تابع التفعيل وحدة التصحيح الخطي وطبقة الخرج كاملة الاتصال مطبّق عليها تابع التفعيل سوفت ماكس softmax فيها عشرة عصبونات وذلك لأنه لدينا عشرة أصناف.
ملاحظة: يمكنك رؤية التّنفيذ في ملفّ DigitClassifier.py في الشفرة البرمجية الخاصّة بالمشروع.
يقوم البرنامج بتدريب النّموذج فقط في التّنفيذ الأوّل، ثمّ يستخدم أوزان النّموذج المدرب والمحفوظة في ملفّ للتنبّؤ بالأرقام.
roi = cv2.resize(digit_image, (28, 28))
roi = roi.astype("float") / 255.0
roi = img_to_array(roi)
roi = np.expand_dims(roi, axis=0)
preds = self.model.predict(roi)
for c in self.exclude_classes:
preds[0][c] = 0
return preds.argmax(axis=1)[0]
يتمّ تحويل الصّورة إلى مصفوفة مناسبة لـشبكة الطيّ العصبونيّة CNN عن طريق التّابع (الصورة إلى مصفوفة) img_to_array بواسطة مكتبة تنسور فلو.
يحتوي البرنامج على مجموعة من المصفوفات المستبعدة، وهي التي لا تُؤخذ بعين الاعتبار في تلك اللعبة (مثلاً الرّقم “0” للعبة السّودوكو غير موجود لأن الأرقام تكون في نطاق [1,9] فقط).
باستخدام [preds.argmax(axis=1)[0 يتمّ أخذ القيمة ذات الاحتماليّة الأعلى لتكون الرّقم الصّحيح.
لاحظ أنّ مجموعة البيانات MINIT هي عبارة عن مجموعة صور تمثل الأرقام المكتوبة بخطّ اليد، بعد تدريبها باستخدام شبكات الطيّ العصبونية CNN فإنها تعطي نتائج بدقّة تصل إلى %99، ولكننا قد واجهنا بعض الأخطاء والمشاكل أثناء استخدامها وذلك بسبب اختلاف الخطّوط، حيث أنّ الأرقام المطبوعة يمكن أن تكون مختلفة كثيراً عن الأرقام المكتوبة بخطّ اليد. على سبيل المثال الرّقم “4” قد ي9″، والرّقم “3” قد يبدو وكأنّه الرّقم “8”.

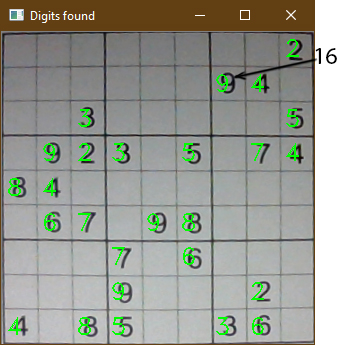
لتسوية هذه المشكلة قرّرنا عدم التّعامل مع الصّورة فقط وإنّما استخدام التنبّؤات أيضاً، تقوم الخوارزميّة بمعرفة أعلى نسبة لكلّ رقم، أي الاكثر تشابهاً له، مثلاً: لاحظ الرّقم 9 في الخلية 16 من الشكل (9)، من المحتمل أن يكون 8 أو 5 أو 3 بنسبة صغيرة وباقي الارقام نسب صغيرة جداً (شبه مستحيل)، ولكن بالنسبة للرّقم 9 نفسه النسبة هي أكبر ماتكون من البقية فعندها نكون متأكدين بأنّ الرّقم هو 9 وليس رقم اخر.. وهكذا لجميع الأرقام.
0:1.7535687e-05, 1:6.7900544e-08, 2:7.2314634e-08, 3:7.1534036e-05, 4:0.0014702848, 5:0.00030473914, 6:1.0657828e-06, 7:2.1889873e-06, 8:0.0014946316, 9:0.9966378
تحليل المكوّنات المتّصلة
بالنسبة للّعبة ستار باتل، لا يوجد أرقام للعثور عليها، إنّما توجد مناطق من الشّبكيّة لتحديدها. يقوم البرنامج بإزالة خطوط الشّبكيّة الداخليّة أوّلاً، ثمّ استخراج المكوّنات المتّصلة.
img = cv2.cvtColor(img.copy(), cv2.COLOR_BGR2GRAY)
kernel = np.ones((6, 6), np.uint8)
img = cv2.erode(img, kernel, iterations=1)
_, img = cv2.threshold(img, 100, 255, cv2.THRESH_BINARY)
num_labels, labels = cv2.connectedComponents(img)
if num_labels == 0:
Return
label_hue = np.uint8(179 * labels / np.max(labels))
blank_ch = 255 * np.ones_like(label_hue)
labeled_img = cv2.merge([label_hue, blank_ch, blank_ch])
labeled_img = cv2.cvtColor(labeled_img, cv2.COLOR_HSV2BGR)
labeled_img[label_hue == 0] = 0
cv2.imshow("Stars Puzzle - Area detection", labeled_img)
في الأسطر الأربعة الأولى نطبّق مرشح (erosion) وذلك لإزالة الخطوط الفاتحة، ثمّ لإبراز حوافّ المناطق نطبّق (threshold). أخيراً نبحث عن المكوّنات المتّصلة، ونلوّن المنطقة بألوان مختلفة.
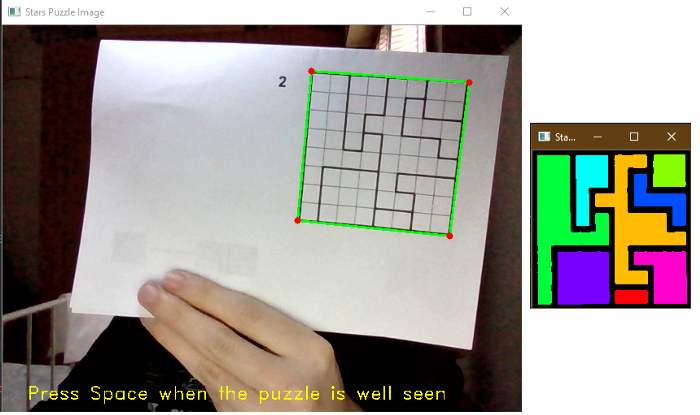
يتمّ تنفيذ البرنامج في الزّمن الحقيقيّ حيث يمكن للمستخدم تأكيد العمليّة (بالضّغط على المسطرة)، عند تأكيد العمليّة يتمّ تجميع خلايا الشّبكية حسب لون البكسل المركزيّ، وتحديد مناطق الألغاز.
الخطوة الثّالثة: حلّ اللغز
نحن الآن نملك جميع العناصر لحلّ اللّعبة، كما في كثيرٍ من ألعاب الألغاز المنطقيّة الأخرى، فإنّ سودوكو وستار باتل والسّكايسكرايبر يمكن وصفها على أنّها مشاكل القيود المرضية (Constraints (Satisfaction Problems. تتكوّن CSP من مجموعة من المتغيرات ومجال من القيم لكل متغير ومجموعة من القيود، الهدف هو تعيين قيمة لكلّ متغير بحيث يتمّ استيفاء جميع القيود.
يتكوّن ال CSP من ثلاثة عناصر:
- مجموعة من المتغيّرات التي نريد إيجاد القيمة الصّحيحة لها.
- مجال للقيم الممكنة لكلّ متغيّر.
- مجموعة من القيود التي تحدّد المشكلة.
على سبيل المثال للعبة السّودوكو نملك:
- المتغيّرات: 81 خليّة من رقعة اللعب (9*9).
- المجالات : المجال {1,9} (باستثناء الخلايا المملوءة بالفعل).
- القيود: قواعد اللّعبة.
يمكن استخدام تمثيلٍ مشابه للعديد من المشكلات والألعاب، بالإضافة الى السّكايسكرايبر وستار باتل، ومع ذلك هناك خصوصيّة: مجال الخلايا هو {0,1} حيث أنّ (1) يمثّل وجود النّجم والـ (0) يمثّل غيابه، الحلّ هو تخصيص معيّن للمتغيّرات بحيث يكون لكلّ قيد قيمة محقّقة.
إنّ الشّفرة البرمجيّة الخاصّة بهذه العمليّة طويلة بعض الشيء (لاحظ الصّف Solver المدرج في المشروع) ولكنّنا الآن سنقوم بشرح فكرة البحث المتكرّر العكسيّ المستخدم في حلّ CSPs في البرنامج، مع إظهار الجزء الأساسيّ من الخوارزميّة.
def recursive_backtracking(self, assignment, csp):
if self.is_complete(assignment):
if not self.there_are_enough_values(assignment):
return "FAILURE"
return assignment
var = self.select_unassigned_variable(csp["VARIABLES"], assignment)
domains_copy = {}
for v in self.CSP['VARIABLES']:
domains_copy[v] = csp["DOMAINS"][v]
domain = self.neighbors_heuristic(assignment, domains_copy, var)
for value in domain:
assignment[var] = value
if self.is_consistent(assignment, csp["CONSTRAINTS"]):
result = self.recursive_backtracking(assignment, csp)
if result != "FAILURE":
return result
assignment[var] = None
return "FAILURE"
قد يبدومعقداً لكنّ فكرته بسيطة للغاية: تقوم الخوارزميّة بالبحث عن الحلّ عن طريق تحديد assignment وهو متغيّر فرديّ (single-variable)، وتبدأ عملية البحث (تقنيّاً هو البحث في العمق أوّلاً depth-first-search) حتى يجد assignment مكتملة (يتحکّم بها باستخدام الطّريقة is-complete) .
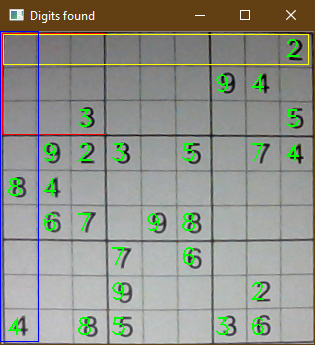
في كلّ خطوة تأخذ الخوارزميّة متغيّراً دون تهيئته بقيمة معينة (select_unassigned_variable) وتختار قيمةً غير مُثبتة ضمن مجالها، مثلاً: لاحظ الشكل (11) تبدأ الخوارزميّة باختيار الرّقم 1 من أجل الخلية الأولى في الرّقعة، ثم تبدأ البحث هل هناك أيّة خلايا بنفس الرّقعة الصغيرة (المربع في اللون الأحمر) قد اختارت هذا الرقم مسبقاً، إذا نعم تختار الرقم التالي ضمن المجال {1,9} أي الرقم 2 في مثالنا هنا، وإلا تبدأ البحث بكامل الرقعة لنفس السطر(المستطيل باللون الأصفر) هل هناك أية خلايا قد اختارت هذا الرّقم مسبقاً نفس المناقشة تختار الرقم التالي مثلاً 3، وإلا تبدأ البحث بكامل الرّقعة لنفس العمود (المستطيل باللون الأزرق)، في مثالنا فإن الرقم 1 لايحوي أي مشاكل حيث أنه بنفس الرقعة الصغيرة لاتوجد خلية أخرى قد اختارت الرقم 1 مسبقاً، كما أن تقاطع السطر والعمود لايحوي أي خلايا قد اختار الرقم 1 مسبقاً، عندها يعتمده ويكمل الحل، أي ستتابع ماذا سوف يحدث، إذا كان الأمر يتعلّق بإحدى الخلايا الأخرى، فإنّ الحالة الحاليّة تحترم جميع القيود (التابع is_consistent) ونستدعي الخوارزميّة مرةً أخرى للتّحقق ممّا إذا كانت المهمّة قد اكتملت، وإلّا فإنّنا نزيل المتغيّر ونعود للحالة السّابقة لمحاولة استخدام قيمٍ مختلفة.
ملاحظة: عندما نقول اكتملت أي لم يكن هناك أيّة تعارضاتٍ كما ناقشنا مسبقاً، في المثال إن الحلّ الأمثل للخلية الأولى هو الرّقم 1 إلى الآن، أي هذا لا يعني بأنه الحلّ النهائي بعد، ولكنه الحل الأمثل ، إنّ الخوارزمية تراجعيّة وبالتالي سوف تعيد عمليات البحث وتغير القيم ربما آلاف المرّات، إلى أن تصل لإيجاد الحلّ المناسب لكامل الرّقعة، عندها فقط نستطيع القول بأنه الحلّ الأمثل لهذه الخلية.
عزيزي القارئ، قم بقراءة كامل الكود وستلاحظ بأنّنا استخدمنا بعض الأساليب الاستدلاليّة لتسريع عمليّة الحل، إحداها الاستدلال السهل easy_inference عند محاولة تعيين بعض المتغيّرات عن طريق التّحقق ممّا إذا كان يمكن إجراء بعض الاستدلالات السّهلة، على سبيل المثال بالنسبة للعبة سودوكو إذا كان هناك صفّ أو عامود أو مربّع يحتوي على ثمانیة قيم واضحة وهي القيمة المفقودة، يتمّ استخدام طريقة أخرى لتحديد القيمة لمتغيّر معيّن.
التّابع Neighbors_heuristic يقوم بحذف بعض القيم من مجالٍ متغيّر معيّن، إذا كان اختيار هذه القيمة يكسر بعض قواعد اللّعبة.
من وجهة نظرٍ حسابيّة، تقلّل الخوارزميّة مساحة البحث من (O(d^n!) إلی O(d^n وهو ليس سيئاً، ولكن من المهمّ الانتباه إلى أنّ الخوارزميّة يمكن أن تكون بطيئةً جداً بدون الاستدلال.
والآن عزيزي بإمكانك أن تطلع على كامل الشفرة البرمجية في مستودع الجت هب الخاص بمدونة الذكاء الاصطناعي باللغة العربية.
الخلاصة :
نعيش في زمنٍ لا يوجد فيه شيء قادر على إدهاشنا، إذ يؤثّر الذّكاء الاصطناعيّ على المجتمع الذي نعيش فيه حتی أصبحنا غير مبالين بالتّكنولوجيا الجديدة، ويجب علينا في بعض الأحيان أن نتوقّف ونفکّر كم نحن محظوظون للعيش في عصر التكنولوجيا المتسارعة.
لنأخذ هذا المشروع البسيط كمثالٍ لنهاية هذه المقالة.
يستخدم البرنامج (حوالي 50 كيلوبايت من الذّاكرة الموزّعة على 4 ملفات) خوارزميّات الرؤية الحاسوبيّة لتحليل الصّور وتحويل المنظور، وشبكة طيّ عصبونية لتصنيف الأرقام، وخوارزميّة لحلّ مشكلة منطقيّة في بضع ثوانٍ قد تستغرق بضعَ دقائق على الأقلّ.
كلّ واحدةٍ من هذه الخوارزميّات هي ثمرةُ عقود من الدّراسة والتّجريب حول العالم، وذلك هو الإرث لأجيال كاملة من العلماء، کما أنّه يتيح لنا امتلاك الأدوات العلميّة والنّظريّة لحلّ المشكلات التي لم نتخيّل حتى وقت قريب القدرة على حلّها.
وبهذه الطّريقة، فإنّ هذا المشروع والآلاف من مشاريع الرؤية الحاسوبيّة والذّكاء الاصطناعيّ الأخرى التي يمكن العثور عليها على مواقع الويب، لاتبدو وكأنّها مجرّد حسابات أو أكواد أو صيغ رياضيّة، وإنّما تبدو وكأنّها أقرب إلى السّحر.