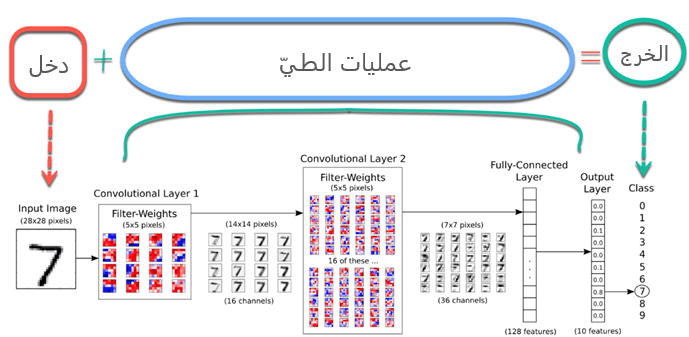
عمل الباحثون على سد الفجوة بين قدرات البشر والآلة ضمن عدة مجالات منها مجال الرؤية الحاسوبية حيث قاموا باستخدام المعرفة في العديد من المهام كالتعرف على الصور وتحليلها وتصنيفها ومجالات أخرى مثل معالجة اللغات الطبيعية، محققين بذلك العديد من التطورات منها إيجاد أقوى تقنيات التعلم العميق الخاضعة للإشراف وهي شبكات الطي العصبونية. البنية النهائية لهذه الشبكات قريبة جدًا من الشبكات العصبونية الاعتيادية RegularNets فهي تحوي عصبونات ذات أوزان و انحيازات و تستخدم تابع خسارة كالانتروبية المتقطعة crossentropy أوسوفت ماكس softmax وكذلك محسًن مثل آدم adam. لكن في شبكات الطيّ العصبونية هناك طبقات إضافية هي طبقات الطي Convolutional Layers و التجميع Pooling Layers و المسطحة Flatten Layers.
المحتويات
لماذا شبكات الطي العصبونية؟
في البنية الأساسية للشبكات الاعتيادية جميع العصبونات متصلة مع بعضها البعض. مثلًأ في حال كان لدينا صور بأبعاد 28×28 بيكسل وبتدرج رمادي فقط سيكون لدينا بالمقابل 784(28x28x1) عصبون في الطبقة التي سيكون من الممكن ضبطها. لكن معظم الصور ليست بتدرج رمادي وتحوي بكسلات أكثر بكثير لذلك وعلى فرض لدينا مجموعة من الصور الملونة عالية الجودة 4K Ultra HD سيكون لدينا بالمقابل 26,542,080 (4096X 2160×2) عصبون مختلف متصلين جميعا ببعضها البعض في الطبقة الأولى والتي لن يكون من الممكن ضبطها في هذه الحالة. بهذا يمكننا القول بأن الشبكات الاعتيادية لا يمكن تطبيقها في تصنيف الصور لأنه وخاصة عندما يتعلق الأمر بالصور سيكون هناك ترابط وصلة قليلة بين بكسلين فرديين مالم يكونوا قريبين من بعضهما البعض. هذا ما أدى إلى فكرة طبقات الطي والتجميع.
الطبقات في شبكات الطيّ العصبونية
في شبكات الطيّ العصبونية نستطيع استخدام العديد من الطبقات المختلفة لكن طبقات الطي والتجميع والطبقات كاملة الاتصال هم الطبقات الأكثر أهمية لذلك سنتحدث عنهم بشكل سريع قبل استخدامهم.
1- طبقات الطيّ
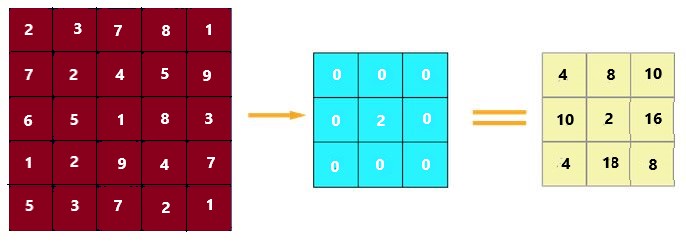
تعتبر هذه الطبقة هي أول طبقة يتم فيها استخراج المزايا من الصور في مجموعة البيانات ونظرًا لحقيقة أن البيكسلات ترتبط فقط بالبيكسلات المجاورة القريبة، يسمح الطيّ بالحفاظ على العلاقة بين أجزاء مختلفة من الصورة. حيث يعمل على ترشيح الصورة باستخدام مرشح بيكسل مصغّر لانقاص حجم الصورة دون فقد العلاقة بين البيكسلات.
عند تطبيق الطيّ على صورة بأبعاد 5×5 باستخدام مرشح 3×3 بخطوة تحريك 1×1 (إزاحة بيكسل واحد في كل خطوة). سنحصل على خرج بأبعاد 3×3 أي إنقاص نسبة التعقيد بمقدار 64%.
2- طبقة التجميع
من الشائع عند بناء شبكات الطيّ العصبونية إدراج طبقات التجميع بعد كل طبقة طيّ وذلك لتقليل حجم فضاء التمثيل بالتالي تقليل عدد المعاملات والذي يقلل من التعقيد الحسابي. كما أن طبقات التجميع تساعد أيضًا في حل مشكلة الملاءمة الزائدة overfitting.
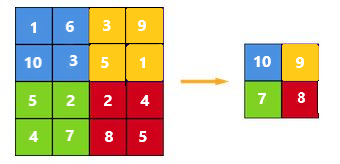
يتم بشكل أساسي اختيار حجم التجميع لتقليل حجم المعاملات باختيار أعظم أو متوسط أو مجموع القيم داخل هذه البيكسلات. يعتبر التجميع باستخدام القيمة العظمى Max Pooling أحد أكثر تقنيات التجميع شيوعَأ. وهي موضحة في الشكل(2)
3- الطبقات كاملة الاتصال
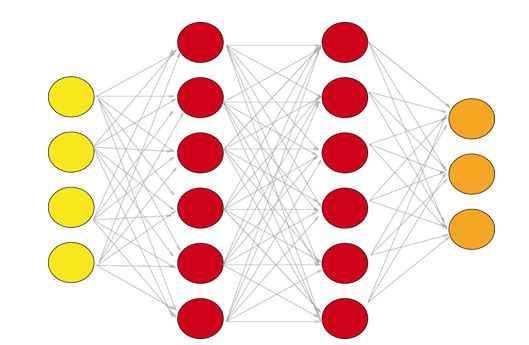
إن الشبكة كاملة الاتصال هي شبكة اعتيادية حيث كل معامل متصل بمعامل آخر لتحديد العلاقة الحقيقية وتأثير كل معامل على التصنيف. ونظرًا لانخفاض تعقيد المساحة الزمنية بشكل كبير بفضل طبقات الطي والتجميع يمكن إنشاء شبكة كاملة الاتصال لتصنيف الصور. مجموعة الطبقات كاملة الاتصال تظهر كما في الشكل(3).
بعد أن أصبح لدينا فكرة عن كافة الطبقات التي سيتم استخدامها سنلقي نظرة على شبكة طيّ عصبونية كاملة كما في الشكل (4)
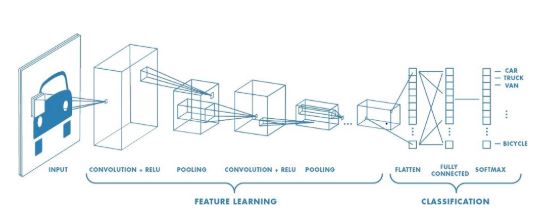
وبعد التعرف على شبكة الطيّ العصبونية التي يمكن إنشاؤها لتصنيف الصور. سنبدأ بتحميل مجموعة البيانات الأكثر استخدامًا للتصنيف وهي إم. نيست والتي تمثل قاعدة بيانات المعهد الوطني للمعايير والتكنولوجيا المعدّلة. وهي قاعدة بيانات كبيرة من الأرقام المكتوبة بخط اليد والتي تستخدم عادة لتدريب أنظمة معالجة الصور المختلفة.
تحميل مجموعة البيانات إم. نيست
تعد مجموعة البيانات إم. نيست واحدة من مجموعات البيانات الأكثر شيوعًا المستخدمة لتصنيف الصور ويمكن الوصول إليها من العديد من المصادر المختلفة. حتى تنسرفلو Tensorflow و كيراس Keras يسمحان لنا باستيرادها وتنزيلها مباشرة من واجهة برمجة التطبيقات. لذلك، سنبدأ بالسطرين التاليين لاستيراد تينسرفلو و إم. نيست ضمن واجهة برمجة تطبيقات.
import tensorflow as tf
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
تحتوي مجموعة بيانات إم. نيست على ستين ألف صورة تدريب وعشر آلاف صورة اختبار مأخوذة من موظفي مكتب الإحصاء الأمريكي وطلاب مدارس الثانوية الأمريكية. لذلك في السطر الثاني قمنا بفصل هذه المجموعتين كمجموعة تدريب وأخرى اختبار وأيضًا فصل الأصناف عن الصور. تحوي x_train و x_test على رموز أر جي بي RGB باللون الرمادي من الـ 0 إلى 255.بينما تحتوي y_train و y_test على التصنيفات من الـ 0 إلى 9 والتي تمثل العدد الفعلي. لرسم هذه الأرقام سنستخدم مكتبة ماتبلوت matplotlib.
import matplotlib.pyplot as plt
%matplotlib inline # Only use this if using iPython
image_index = 7777 # You may select anything up to 60,000
print(y_train[image_index]) # The label is 8
plt.imshow(x_train[image_index], cmap='Greys')
عند تنفيذ الشيفرة البرمجية السابقة سنحصل على الرسم باللون الرمادي لرموز أر جي بي كما في الشكل التالي.
يجب معرفة شكل مجموعة البيانات لتوجيهها إلى شبكة الطيّ العصبونية. لذلك سنستخدم الخاصية “Shape” من مصفوفة بايثون العددية numpy من خلال سطر الشيفرة البرمجية التالي.
x_train.shape
بتنفيذ ما سبق ستكون النتيجة (60000, 28, 28). الرقم 6000 يمثل عدد الصور في مجموعة التدريب بينما (28×28) تمثل أبعاد الصورة وهي 28×28 بيكلسل
إعادة تشكيل وتقييس الصور Normalizing
لنستطيع استخدام مجموعة البيانات في واجهة تطبيقات كيراس Keras API سنحتاج إلى مصفوفة بأربع أبعاد. لكن كما رأينا أعلى أن مصفوفتنا ثلاثية الأبعاد. بالإضافة يتوجب علينا تقييس البيانات كما هو مطلوب دائمًا في نماذج الشبكات العصبونية. يمكن القيام بذلك من خلال تقسيم رموز أر جي بي على 255 (وهي الحد الأقصى ناقص الحد الأدنى لرموز آر جي بي). يتم تنفيذ ذلك في الأسطر التالي.
# Reshaping the array to 4-dims so that it can work with the Keras API
x_train = x_train.reshape(x_train.shape[0], 28, 28, 1)
x_test = x_test.reshape(x_test.shape[0], 28, 28, 1)
input_shape = (28, 28, 1)
# Making sure that the values are float so that we can get decimal points after division
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
# Normalizing the RGB codes by dividing it to the max RGB value.
x_train /= 255
x_test /= 255
print('x_train shape:', x_train.shape)
print('Number of images in x_train', x_train.shape[0])
print('Number of images in x_test', x_test.shape[0])
والخرج سيكون:
بناء شبكة الطيّ العصبونية
سنقوم ببناء النموذج باستخدام واجهة برمجة تطبيقات كيراس عالية المستوى والتي تستخدم في الخلفية إما تنسرفلو أو ثيانو Theano. من الجدير بالذكر أن هناك العديد من واجهات برمجة التطبيقات لتنسرفلو مثل الطبقات Layers، كيراس، والمقدّر Estimators الذي يساعد على إنشاء شبكات العصبونية ذات معرفة عالية المستوى. و باعتبار أن لكل منهم بنية تطبيق مختلفة لهذا سنرى شيفرات برمجية مختلفة لنفس الشبكة العصبونية على الرغم من أن جميعهم يستخدمون تنسرفلو.
في هذه المدونة سنعتمد على أكثر هذه الواجهات سهولة وهي كيراس. سنبدأ باستيراد النموذج بالشكل التسلسلي (طبقة تلو الأخرى) من كيراس ومن ثم سنضيف كافة الطبقات على الشكل التالي:
- طبقتي طيّ Conv2D
- طبقة تجميع باستخدام القيمة العظمى
- طبقة مسطحة لتسطيح المصفوفات ثنائية البعد إلى مصفوفة ذات بعد وحيد قبل بناء طبقات كاملة الاتصال.
- طبقات تعطيل عمل العصبونات Dropout والتي تقوم بالوقوف ضد الملاءمة الزائدة من خلال تجاهل بعض العصبونات في مرحلة التدريب.
- طبقات كاملة الاتصال Dense layers.
# Importing the required Keras modules containing model and layers
from keras.models import Sequential
from keras.layers import Dense, Conv2D, Dropout, Flatten, MaxPooling2D
# Creating a Sequential Model and adding the layers
model = Sequential()
model.add(Conv2D(28, kernel_size=(3,3), input_shape=input_shape))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Flatten()) # Flattening the 2D arrays for fully connected layers
model.add(Dense(128, activation=tf.nn.relu))
model.add(Dropout(0.2))
model.add(Dense(10,activation=tf.nn.softmax))
سنجرب أي عدد من العصبونات في الطبقة كاملة الاتصال الأولى. أما بالنسبة للطبقة كاملة الإتصال الأخيرة فيجب أن تحتوي عشر عصبونات باعتبار أنه لدينا عشر أرقام للتصنيفات من 0 إلى 9. ربما علينا تجريب أحجام مختلفة لمصفوفة الطيّ kernel size و وكذلك لحجم التجميع pool size وتوابع تفعيل ومعدل تعطيل عمل العصبونات وعدد عصبونات في الطبقة كاملة الاتصال الأولى مختلفة للحصول على أفضل النتائج.
تفسير وملاءمة النموذج
باستخدام الشيفرة البرمجية السابقة قمنا بإنشاء شبكة طيّ عصبونية فارغة غير محسّنة. لذا سنقوم الآن بضبط المحسّن و تابع الخسارة ومن ثم ملاءمة النموذج باستخدام بيانات التدريب وذلك على الشكل التالي.
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
model.fit(x=x_train,y=y_train, epochs=10)
يمكن تجريب تغيير أي من المعاملات السابقة (المحسنّ، تابع الخسارة، الدورة التدريبية،…) لكن يمكن القول أن المجسنّ آدم Adam يتفوق على بقية المحسنات. وقد تبدو دورة التدريب صغيرة نوعًا ما لكننا حصلنا فيها على دقة اختبار 98-99ّ %. وباعتبار أن مجموعة بيانات إم. نيست لا تتطلب طاقة حوسبة ثقيلة يمكن بسهولة تجربة دورة تدريبية مختلفة.
نتيجة تنفيذ الشيفرة البرمجية السابقة هي

تقييم النموذج
أخيرًا يمكن تقييم النموذج المدرب باستخدام مجموعات الاختبار x_test و y_test وذلك كما يلي.
والنتيجة قد تبدو جيدة من أجل عشر دورات تدريبية لهذا النموذج البسيط
بهذا النموذج الأساسي حصلنا على دقة تصل إلى 98.5%. لكن في العديد من حالات تصنيف الصور مثل السيارات ذاتية القيادة لا يمكن تحمل حدوث خطأ بنسبة 0.1 % لأن هذا يعني حدوث حادث واحد في الألف حالة. ومع ذلك بالنسبة لنموذجنا الأولي النتيجة لا تزال جيدة. يمكن إجراء تنبؤات فردية باستخدام الشيفرة البرمجية التالية.
image_index = 4444
plt.imshow(x_test[image_index].reshape(28, 28),cmap='Greys')
pred = model.predict(x_test[image_index].reshape(1, 28, 28, 1))
print(pred.argmax())
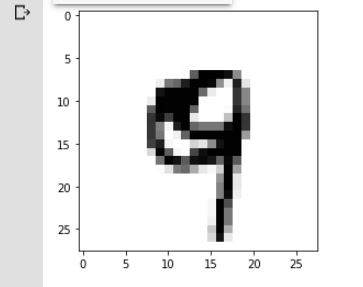
نموذجنا سيصنف الصورة كرقم 9 ويرسم الصورة لها كما في الشكل

على الرغم من أن كتابة اليد ليست بالشكل الجيد للرقم 9، إلا أن النموذج كان قادرًا على تصنيفه على أنه 9.
الخاتمة
قمنا في هذه المدونة بإنشاء شبكة طي عصبونية لتصنيف الأرقام المكتوبة بخط اليد بعد أن بيّنا سبب اختيار هذا النوع من الشبكات وبنيتها الأساسية، تم تصنيف الأرقام باستخدام برمجة تطبيقات كيراس مع تينسرفلو وذلك بعدة خطوات أولًا إنشاء النموذج ثم القيام بعملية تفسيره وملاءمته وأخيرًا مرحلة تقييمه وفيها حصلنا على دقة تفوق 98% وتعتبر هذه القيمة نتيجة جيدة بالنسبة لنموذجنا الأوليّ. يمكن الآن حفظ هذا النموذج وكذلك إنشاء تطبيق لتصنيف الأرقام و لمعرفة كيفية استخدام واجهة برمجة التطبيقات بكفاءة وحفظ النموذج، يجب تعلم كيفية قراءة وثائق كيراس Keras Documentation واستخدامها.
المراجع
[1] KataKoda
[2] CS231n Convolutional Neural Networks for Visual Recognition





