المحتويات
- مجال الرؤية الحاسوبيّة Computer vision وأهميّته
- الرؤية عند الإنسان وعند الحاسوب
- معلومات أساسية
- مبدأ عمليَّة الطيّ convolution
- تنفيذ عمليّة الطيّ في لغة البرمجة بايثون و مكتبة أوبن سيفي OpenCv
- أمثلة على عمليّة الطيّ في بايثون وأوبن سيفي OpenCv
- دور عمليّة الطيّ في التعلُّم العميق Deep Learning
- الخلاصة
- المصادر
مجال الرؤية الحاسوبيّة Computer vision وأهميّته
ربما سمعت عزيزي القارئ في السنوات الأخيرة بـ computer vision والذي يترجم في العربية إلى الرؤية الحاسوبية. وإذا لم تسمع بالمصطلح فإنني أؤكد لك أنك استخدمته وربما حتى أنك تستخدمه يومياً بدون أن تدري من خلال برامج معالجة الصور مثل فوتوشوب Photoshop أو عن طريق العديد من تطبيقات الهواتف الذكيّة مثل فلاتر سناب شات وإنستغرام.
في هذا المقال سوف نتحدّث عن إحدى أهم العمليّات الرياضيّة التي تقف وراء علم معالجة الصور image processing وهي عملية الطّيّ convolution وكيفية تطبيقها على الصور واستخدامها في الرؤية الحاسوبية. كذلك سنرى أمثلة عمليَّة لعمليَّة الطيّ وتطبيقاتها باستخدام لغة البرمجة بايثون Python و استخدام مكتبة تطبيقات الرؤية الحاسوبية أوبن سيفي OpenCv لإجراء عمليّات مختلفة على الصور.
الرؤية عند الإنسان وعند الحاسوب
يتم الإبصار عند الإنسان بطريقة معقدة لم تكشف كل جوانبها إلى الآن. تقوم العين بعكس صورة الوسط المحيط والتي هي عبارة عن ضوء مرئي على الشبكية، حيث تستشعر خلاياها للضوء بتراكيز وألوان مختلفة، وتقوم بدورها بتحويل ذلك إلى سيّالة عصبيّة تنتقل عن طريق العصب البصَريّ إلى الفص الخلفي للمخ ومراكز مخية أخرى. هناك يتم معالجة المعلومات البصريّة عن طريق التعاون بين ملايين من العصبونات في أقسام مختلفة من الدماغ، لمساعدتنا في عمليات حياتيّة يوميّة مألوفة مثل القراءة والتعرّف على الوجوه وإدراك أن سيارة تقترب منّا أثناء القيادة مثلاً أو تبتعد، والكثير الكثير من الأشياء تمنحنا إيّاها القدرة على الأبصار.
ما نفعله اليوم في الرؤية الحاسوبية هو شيء مشابه لعملية الإبصار عند الإنسان، يتفوق ذلك في بعض الحالات على قدرة الإنسان الإبصاريّة بفضل القدرة الحاسوبيّة الضخمة وأحياناً أخرى لا يصل إلى الدقة المطلوبة بسبب القدرة المحدودة للخوارزميّات المستخدمة حاليّاً.
معلومات أساسية
لتبسيط مبدأ عملية الطيّ نحتاج أولا للتعرُّف على مفهومين هما تمثيل الصور رقمياً و مصفوفة الطيّ kernel.
الصورة الرقميّة digital image
الصورة الملوّنة RGB image عبارة عن مصفوفة متعددة الأبعاد تحتوي على ارتفاع وعرض وعمق. كل مربع من مربعات المصفوفة يمثل بكسل pixel. يحتوي كل بكسل على ثلاث قيم لونية (أحمر وأخضر وأزرق) وتأخذ قيم بين 0-256. يمكن لكل بكسل أن يمثل 16777216 لون مختلف.
مصفوفة الطيّ kernel
لو اعتبرنا مصفوفة الطيّ كمصفوفة صغيرة والصورة كمصفوفة كبيرة كما يتبين لنا من الصورة هنا، المصفوفة الصغيرة ذات اللون الأحمر تُمثِّل مصفوفة الطّي kernel، المصفوفة الكبيرة تُمثِّل الصورة. معظم الأحيان تكون نواة الطيّ مصفوفة مربّعة ولكن يمكن أن تكون مختلفة الأبعاد بشرط أن يكون البعدين عددين فرديين لكي نحصل على مصفوفة لها إحداثيات في المنتصف تمثل المركز. الشكل رقم 2 يوضح ذلك.

الشكل (1): عملية الطّي. مصفوفة الطّي موضحة باللون الأحمر [1]
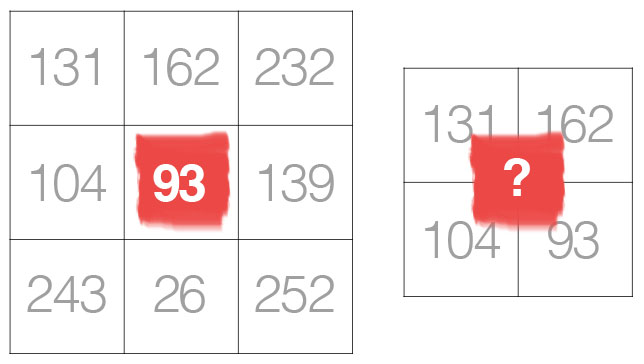
الشكل (٢): مقارنة بين مصفوفتي طيّ، المصفوفة على اليمين ذات أبعاد زوجية مقارنة بالمصفوفة على اليسار ذات الأبعاد الفردية
مبدأ عمليَّة الطيّ convolution
في مجال معالجة الصور تحتاج عمليّة الطيّ إلى ثلاث عناصر رئيسية وهي:
- صورة الدخل input image
- مصفوفة الطيّ kernel
- صورة الخرج output image لتخزين مخرج صورة الدخل التي أُجريت عليها عملية الطّي مع مصفوفة الطّي
الآن ربما تتساءل عزيزي القارئ أنّنا ذكرنا حتى الآن عملية الطيّ بشكل متكرر ولم نعرف بالضّبط ما هي وكيف يتم تطبيقها على الصورة. الطيّ في الحقيقة عمليّة أسهل مما تتوقع بكثير. هي مجرد عملية رياضيَّة يتم من خلالها ضرب مصفوفة الطيّ بجزء من الصورة مقابل لها بنفس الحجم. بعد وضع مصفوفة الطيّ على الصورة يتم ضرب كل حد من حدود مصفوفة الطيّ بالحد المقابل له من الصورة وهكذا تُضرب جميع الحدود ثم تُجمع. نتيجة العملية تُدعى خرج مصفوفة الطيّ، تُوضع في مركز مصفوفة الطيّ وهذه تمثل القيمة التي توضع في صورة الخرج. تُزاح بعد ذلك مصفوفة الطيّ خطوة إلى اليمين وتُعاد عملية الضرب وجمع الحدود على هذا القسم من الصّورة. يُعاد تطبيق هذه العملية على جميع أجزاء صورة الدخل عن طريق إزاحة مصفوفة الطيّ خطوة تليها خطوة من اليسار إلى اليمين ومن الأعلى إلى الأسفل حتى نصل إلى أقصى أسفل اليمين من الصورة.

الشكل (٣): مثال توضيحي يبين كيفية تطبيقة مصفوفة الطي على صورة الدخل [2]
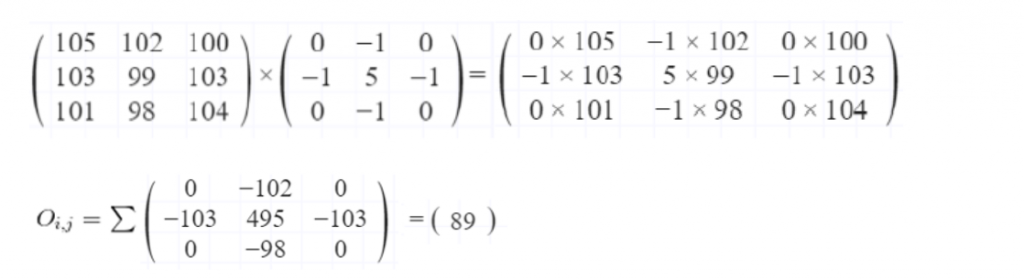
الشكل (٤): في الصورة العلويّة نضرب مصفوفة الطيّ بجزء الصورة المقابل له (كل عدد بمقابله). المصفوفة السفليّة تمثل نتائج الضرب حيث تجمع هذه النتائج لتعطي ناتج الطيّ kernel output وهو 89 في هذا الجزء من الصورة
تنفيذ عمليّة الطيّ في لغة البرمجة بايثون و مكتبة أوبن سيفي OpenCv
بعد أن تعرّفنا على أهم الأسس النظريّة لعمليّة الطيّ سوف نبدأ الآن بالعمل الجدّي لنطبِّق ما تعلّمناه في كود حقيقي يمكِنك أيضاً تنفيذه بنفسك. في البداية نستورد مكتبة بايثون العددية numby و مكتبة أوبن سيفي OpenCv.
# import the necessary packages
from skimage.exposure import rescale_intensity
import numpy as np
import cv2
def convolve(image, kernel):
# grab the spatial dimensions of the image, along with
# the spatial dimensions of the kernel
(iH, iW) = image.shape[:2]
(kH, kW) = kernel.shape[:2]
# allocate memory for the output image, taking care to
# "pad" the borders of the input image so the spatial
# size (i.e., width and height) are not reduced
pad = (kW - 1) // 2
image = cv2.copyMakeBorder(image, pad, pad, pad, pad,
cv2.BORDER_REPLICATE)
output = np.zeros((iH, iW), dtype="float32")
بعد ذلك نبدأ بكتابة دالّة لعمليّة الطيّ convolve function. في السطر 9 و 10 نقوم بتعريف الصورة image و مصفوفة الطيّ kernel على شكل مصفوفة لها بعدين عرض وارتفاع. قبل أن نكمل في ذلك يجب أن ننوه على نقطة وهي أنه خلال عمليّة الطيّ يتم فقد جزء من أبعاد الصورة الأصليّة. يكون هذا الاختزال أحياناً مرغوب به، لكن نحتاج معظم الأحيان لصورة الخرج أن تكون لها نفس أبعاد صوره الدخل. تُطلق على عملية ملئ الأبعاد المختزلة بالحشو padding. في السطر 15 نقوم بتعريف متغير pad بحيث يعطينا الأبعاد المختزلة من كل جانب من جوانب الصورة اعتماداً على عرض مصفوفة الطيّ. يمكن أن يتم الحشو بملئ هذه الفراغات بأصفار أو كما سنقوم نحن في المثال بنسخ القيم الموجودة في المربعات المجاورة ووضعها في المربعات الفارغة في السطر 16 و 17. في السطر 18 نُعرِّف صورة الخرج output على شكل مصفوفة أصفار ثنائيّة الأبعاد باستخدام مكتبة بايثون العددية numby. سوف تُملأ هذه المصفوفة لاحقاً بقيم خرج مصفوفة الطّي.
# loop over the input image, "sliding" the kernel across
# each (x, y)-coordinate from left-to-right and top to
# bottom
for y in np.arange(pad, iH + pad):
for x in np.arange(pad, iW + pad):
# extract the ROI of the image by extracting the
# *center* region of the current (x, y)-coordinates
# dimensions
roi = image[y - pad:y + pad + 1, x - pad:x + pad + 1]
# perform the actual convolution by taking the
# element-wise multiplicate between the ROI and
# the kernel, then summing the matrix
k = (roi * kernel).sum()
# store the convolved value in the output (x,y)-
# coordinate of the output image
output[y - pad, x - pad] = k
نحن الآن مستمرون بكتابة دالّة لعمليَّة الطيّ. دعونا نرجع قليلاً لنتذكر ماقلناه سابقاً بخصوص عمليَّة الطَّيّ. نحتاج عمليَّاً لكود يُمكِّننا من إزاحة نواة الطيّ على الصورة من الأعلى إلى الأسفل ومن اليسار إلى اليمين وفي كل إزاحة نضرب عناصر نواة الطَي بالعناصر المقابلة لها من الصورة. هذه العمليَّة التي تبدو معقّدة تُنفَّذ في الواقع ببضعة أسطر في بايثون. يُستخرج في كل دورة من الحلقة loop جزء من الصورة بحجم مصفوفة الطّي يُمثِّلها المتغيِّر roi. بعد ذلك يُضرب هذا الجزء من الصورة بنواة الطيّ والتي تمثِّل عمليَّاً مصفوفة. تُجمع هذه الحدود سوياً وتُخزَّن في المتغيِّر k. سوف نُعرِّف قيم مصفوفة الطيّ لاحقاً ضمن الكود. توضع قيمة k في صورة الخرج بالمكان المُمثِّل لمركز مصفوفة الطيّ. يظهر ذلك بعملية الطرح ( y – pad).
# rescale the output image to be in the range [0, 255]
output = rescale_intensity(output, in_range=(0, 255))
output = (output * 255).astype("uint8")
# return the output image
return output
هل تتذكرون قبل قليل في حديثنا عن الصور الملوّنة وتمثيلها رقمياً. يحتوي كل بكسل في الصور غير الملوّنة فقط على رقم بين 0-256 يمثِّل التركيز من الأبيض إلى الأسود. عند ضرب مصفوفة الطيّ بجزء الصورة المقابل لها يُمكن أن نحصل على أرقام أكبر من 256. للحصول فقط على أرقام في المجال المسموح به، نقوم بإعادة قياس rescale عن طريق الدالّة rescale_intensity في السطر 40. في السطر الذي يليه نُحوِّل نمط متغيِّر صورة الخرج من أرقام الفاصلة العائمة الحقيقية float point إلى الأرقام الصحيحة الغير مؤشَّرة unsigned integer.
# construct average blurring kernels used to smooth an image
smallBlur = np.ones((7, 7), dtype="float") * (1.0 / (7 * 7))
largeBlur = np.ones((21, 21), dtype="float") * (1.0 / (21 * 21))
# construct a sharpening filter
sharpen = np.array((
[0, -1, 0],
[-1, 5, -1],
[0, -1, 0]), dtype="int")
# construct the Laplacian kernel used to detect edge-like
# regions of an image
laplacian = np.array((
[0, 1, 0],
[1, -4, 1],
[0, 1, 0]), dtype="int")
# construct the Sobel x-axis kernel
sobelX = np.array((
[-1, 0, 1],
[-2, 0, 2],
[-1, 0, 1]), dtype="int")
# construct the Sobel y-axis kernel
sobelY = np.array((
[-1, -2, -1],
[0, 0, 0],
[1, 2, 1]), dtype="int")
# construct the kernel bank, a list of kernels we're going
# to apply using both our custom `convole` function and
# OpenCV's `filter2D` function
kernelBank = (
("small_blur", smallBlur),
("large_blur", largeBlur),
("sharpen", sharpen),
("laplacian", laplacian),
("sobel_x", sobelX),
("sobel_y", sobelY)
)
في هذا القسم من الكود نبدأ بتعريف مصفوفات الطيّ التي نريد تطبيقها على الصور. في البداية نُعرِّف مصفوفتين للتغبيش blurring واحدة صغيرة وواحدة كبيرة. سيظهر لنا لاحقاً عند تطبيق الكود أن تأثير التغبيش من مصفوفة الطيّ الكبيرة أكبر من المصفوفة الصغيرة. يلي ذلك تعريف مصفوفة لابلاس laplacian kernel التي تفيدنا بكشف الحواف edge detection. ثم لدينا مصفوفة sobelX ومصفوفة sobelY التي تستخدم أيضاً في كشف الحواف العمودية والعرضية. سوف لن نتحدث بالتفصيل في هذه المقال عن كيفيَّة تشكيل مصفوفات الطّي وعلاقة الأرقام بالوظائف التي تقوم بها، نحتاج لهذا الغرض لمقال خاص. إذا أردتم التوسع في ذلك يمكِنكم في هذا الرابط التّجريب واللّعب بمصفوفات الطّي كيفما شئتم ورؤية نتائج ذلك مباشرة على الصور http://setosa.io/ev/image-kernels/. أخيراً في السطر 78 نُعرِّف متغيّر kernel Bank يحتوي جميع مصفوفات الطّي المُعرَّفة سابقاً.
# load the input image and convert it to grayscale
image = cv2.imread("flowers.jpg",1)
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
from google.colab.patches import cv2_imshow
# loop over the kernels
for (kernelName, kernel) in kernelBank:
# apply the kernel to the grayscale image using both
# our custom `convole` function and OpenCV's `filter2D`
# function
print("[INFO] applying {} kernel".format(kernelName))
convoleOutput = convolve(gray, kernel)
opencvOutput = cv2.filter2D(gray, -1, kernel)
# show the output images
cv2_imshow(gray)
cv2_imshow(convoleOutput)
cv2_imshow(opencvOutput)
cv2.waitKey(0)
cv2.destroyAllWindows()
في الجزء الأخير من الكود نستورد الصورة التي نريد. تُقرأ الصورة في السطر 87 بعد رفعها على CoLab. نُطبِّق على الصورة عمليّة الطّي بدءاً من السطر 92 حتى 98، أوّلاً من خلال الدالّة التي عرّفناها سابقاً ()convolve ثمّ من خلال الدالّة الجاهزة filter2D في مكتبة أوبن سيفي OpenCv. تُطبَّق هاتين الدالّتين من خلال حلقة loop على جميع مصفوفات الطيّ المعرّفة مسبقاً ضِمن KernelBank. في السطر 101 نعرض الصورة الأصليّة غير الملوّنة ثم نعرض النتائج على الشاشة ونقارن بينهما. فقط عليك عزيزي القارئ أن ترفع الصورة على CoLab. إذا نسخت الكود أعلاه و غيَّرت إسم الصورة في السطر 87 ونفَّذت الكود run ستظهر لك جميع النتائج التي عملنا عليها وترى أنَّه لا فرق بين دالّة الطيّ التي عرّفناها بأنفسنا وبين الدالّة الجاهزة filter2D في OpenCv.
أمثلة على عمليّة الطيّ في بايثون وأوبن سيفي OpenCv
بعد تنفيذي للكود الذي في الأعلى على صورة قد وجدتُّها على شبكة الإنترنت كما يظهر أدناه، سنرى النتائج المرجوّة مطبَّقة على هذه الصورة وتأثير مصفوفات الطّي عليها.

الشكل (٥): الصورة الأصليَّة في اليسار. ستُقرأ من خلال الكود وتُحوَّل إلى صورة غير ملوَّنة كما في اليمين. سوف نُطبق على الصورة في اليمين مصفوفات الطيّ التي عرّفناها سابقاُ.


الشكل (٧): تطبيق مصفوفة تغبيش كبيرة large blurring على الصورة

الشكل (٨): تطبيق مصفوفة تنعيم sharpening kernel على الصورة

الشكل (٩): تطبيق مصفوفة طيّ لابلاس laplacian kernel على الصورة لكشف الحواف edge detection

الشكل (١٠): تطبيق مصفوفة الطيّ sobel_x على الصورة لكشف الحدود العموديّة

الشكل (١١): تطبيق مصفوفة الطيّ sobel_y على الصورة لكشف الحدود الأفقية
دور عمليّة الطيّ في التعلُّم العميق Deep Learning
كما رأينا في المقال إلى الآن يجب علينا لتنفيذ عمليات على الصورة مثل التغبيش والتنعيم وكشف الحواف أن نُحدِّد القيم التي بداخل مصفوفة الطيّ بأنفسنا.
السؤال الذي يطرح نفسه هنا، هل يمكننا أن نُعرِّف خوارزميَّة في مجال التعلم الآلي machine learning يُمكن لها أن تتعلَّم بنفسها بناء مرشحات لعمليّات مختلفة بدلاً من تحديد كل القيم بشكل يدوي.
في الحقيقة الجواب على هذا السؤال هو نعم. يوجد خوارزميّات في مجال الشبكات العصبونيَّة neural networks يطلق عليها شبكات الطّي العصبونيّة convolutional neural networks. يمكن لهذه الشبكات عن طريق استخدام تقنيّات متعددة مثل التجميع pooling، مرشحات الطّي convolutional filters و توابع التفعيل غير الخطيّة nonlinear activation function يمكن لها أن تتعلّم تشكيل مرشحات قادرة على كشف الحواف في الطبقات الدنيا من الشبكة واستخدام هذه الحواف لكشف بنى أكثر تعقيداً في الطبقات العميقة من الشبكة مثل وجه أو قطة أو كلب.
الخلاصة
في مقال اليوم بدأنا بالتحدّث عن الصور الرقميَّة وطريقة تمثيلها في الحاسوب. تحدّثَنا أيضاً عن موضوعنا الأساسيّ وهو عمليّة الطيّ التي تبيّن لنا أنَها عمليّة رياضيّة بين الصورة ومصفوفة الطّي. حيث تُمثَّل عمليّة الطّي من خلال إزاحة وضرب عناصر مصفوفة الطيّ مع صورة الدخل. ثمّ توضع نتائج هذه العمليّة في صورة الخرج. حدود مصفوفة الطيّ هي التي تحدّد نوع العملية التي نريد إجرائها على الصورة. مررنا بالحشو وتعلّمنا كيفيّة تنفيذه في بايثون. كذلك قمنا بكتابة كود كامل في بايثون لتنفيذ عمليّة الطيّ. بعد ذلك رأينا بعض الأمثلة العمليَّة لعمليَّة الطيّ والفرق بين الكود الذي كتبناه والدالّة الجاهزة function في مكتبة أوبن سيفي OpenCv. تطرّقنا أخيراً إلى بعض التطبيقات الممكنة لعمليّة الـطيّ في التعلّم العميق. في النّهاية يمكن أن أقول إن ما تعلّمناها اليوم هو أحد اللَّبِنات الأساسيّة لفهم علم من أكثر المجالات التقنية تطوّراً حالياً و مليء بالتطبيقات المختلفة في مجالات عديدة.






تعليق واحد