المقدمة Introduction
شاهدنا جميعاً الأشجار منذُ طفولتنا، لها جذر وفوقه الفروع فالأوراق، وفي حال تَتَبُّعِنا كلُّ ورقةٍَ من الأوراقِ حتى الجذر نجد أنَّ لها مساراً وحيداً، لكن أن نرَ الجذر في الأعلى والأوراق في الأسفل فإمَّا أنَّنا نحن من نقف بشكلٍ مقلوب أو أنَّنا نُشاهد الأشجار ضمن علوم الحاسب حيث أنَّ الخوارزمياتِ الحاسوبيَّة استَخدَمت البُنيَة الشجريّة لعمليَّات البحث والفرز، وفي مجالِ تعلُّم الآلة كان استخدامها لتصنيف البيانات وإيجاد القرار فسُمِّيت بأشجار القرار.
شجرةُ القرارِ هي أحد طرقِ تعلُّم الآلة من نوع التعلُّم بإشراف “Supervised” تُستخدم في مشاكلِ التصنيف “Classification” والانحدار “Regression”، تُنتِج خوارزميَّات أشجارِ القرار مجموعةً من قواعد القرار “Decision Rules” الَّتي من خلالها يتمّ إيجاد الصنف(نتيجة الاختبار)، تُبنى على مبدأ التقسيم إلى عقدٍ من الأعلى إلى الأسفل فتُقسَّم مجموعة البيانات إلى مجموعاتٍ فرعيَّة أصغر وأصغر حتَّى الوصول إلى عقد الهدف(الصنف)، حيثُ تبدأ من عقدةِ الجذر الّتي تحوي جميع السِّجلَّات، ثمَّ تقوم بالتَّقسيم بحسب عمود التَّصنيف “Class Label”(هو العمود الذي يُبنى عليه التَّصنيف)، أمَّا بالنِّسبة لخوارزميَّاتها فلها الكثير من الأنواع بحسب مجموعة البيانات، فعلى سبيل المثال: إذا كانت البيانات ذاتُ طابعٍ اسميٍّ يمكنك استخدام خوارزميَّة ID3، أمَّا البيانات ذاتُ القيم العدديَّة المستمرَّة فخوارزميَّة C4.5 تُناسبها أكثر، وطرق أشجار القرار لا تحتاج إلى معاملات(أي أنَّ خوارزميَّاتها لا تملك مُعاملات خاصَّة وإنَّما فقط خطواتٌ لعمليَّة التَّقسيم وفق مبدأ النَّقاء “Purity” للعقدة).[3]
تُعرَف العقدة العلويَّة في شجرةِ القرار بعقدةِ الجذر “Root Node”.
وتُعرَف العقدة الفرعيَّة الَّتي تَنقَسم إلى عقدٍ فرعيَّةٍ أُخرى بعقدةِ القرار “Decision Node”.
أمَّا العقد الَّتي لا تنقسم تُسمّى عقدة الورقة “Leaf Node” وهي تُعتبر نهاية هذا الفرع من الشَّجرة.[3]
المَحتويَات
مبدأ عمل اشجار القرار
تأخُذ البيانات على شكل عقدة ثمَّ تقوم بتقسيمها إلى عقدٍ أُخرى أصغر بحسب سمة(عمود) التقسيم، تبدأ من عقدة الجذر ثمَّ تنقسم البيانات إلى العقد الفرعيَّة وتُعاود الانقسام إلى عقدٍ فرعيَّةٍ أخرى وصولاً إلى العقدة الورقة الَّتي تعطينا التَّصنيف هذا شجريَّاً أمَّا بيانيَّاً يكون التَّصنيف عبارة عن إضافة لخطٍ مستقيمٍ مراراً وتكراراً للحصول على حدود القرار وهذه العمليَّة تدعى الانقسام “Splitting”، قد ندخل في حالة المُلاءمة الزَّائِدة “Overfitting” لأنَّنا نأخذ بعين الاعتبار جميع السِّجلات، وقد تحوي البيانات ضجيجاً(قيم شاذَّة) لذا نستخدم مبدأ التَّقليم “Pruning” لتخفيض تلك المُلاءمة غير المرغوبة.
1_الانقسام Splitting
هي عمليَّة تقسيم لمجموعة البيانات في كلِّ عقدةٍ إلى عقدتين(مجموعتين) أو أكثر بحسب واصفات السِّمة(العمود) في المستوى التَّالي[1]، وعمليَّة التَّقسيم تُبنى على مقياسين:
1_1_مقياس العشوائيَّة “الانتروبيَّة” Entropy
ابتكر هذا المفهوم أحد روَّاد المعلومات النَّظريَّة كلود شانون[4] والمفهوم الأساسي للانتروبيَّة هو قياس لمقدار الفوضى الموجودة في نظامٍ ما، وهنا يدُل المقياس على مقدار(احتمال) التَّبايُن في العقدة “أي هل العقدة تحوي أكثر من صنف؟” وبما أنَّه احتمال فهو يتراوح بين [0,1]، فإذا كانت الانتروبيّة تساوي 0 فإنَّ مجموعة البيانات الفرعيَّة في هذه العقدة نقيَّة “أي أنَّها من صنفٍ واحدٍ فقط”، أمَّا في حال كانت تساوي 1 أو قريبةً منه فهذا يعني أنَّ العشوائيَّة عاليةٌ “أي أنَّها تحوي بياناتٍ من أكثر من صنف ومازالت بحاجة لتقسيم”، معادلتها:
En=∑0→n((s1+..+sm)/S)*I(s1..sm)
حيث: n عدد القيم المميِّزة للعمود(واصفات)، s1..sm القيم الخاصَّة بالقيمة المميِّزة(بالواصفات)، S عدد أسطر الجدول، I كميّة المعلومات للقيمة المميِّزة.
وتُحسب كميَّة المعلومات من العلاقة:
I(s1…sm)=-∑0→n((si/S)*log2(si/S))
إضاءة علميَّة
تَستَخدِم الانتروبيَّة اللُّوغاريتم في حال كان النِّظام الَّذي يُدرس ذو احتماليَّة متساوية أي الاحتمالات ضمنه متجانسة ويكمن سر استخدام اللوغاريتم باعطاء أقل عدد مرَّات للوصول إلى النَّتيجة، كمثال علميّ: في حال طُلب اختيار رقم من 1 إلى 30 ثمَّ أردنا الكشف عن ذلك الرقم بطرح عدّة أسئلة فإنَّ أكبر عدد للأسئلة هو السُّؤال عن كل رقم أي لدينا 30 سؤال في أسوأ الأحوال، بينما في حال قمنا بالسؤال _هل العدد أقل من 15 ؟_، أيَّا كانت الإجابة نعم أو لا نكون قد اختصرنا نصف عدد الأسئِلة أي سرّعنا من احتماليَّة الوصول للرقم وخفَّضنا 15 سؤالاً بسؤالٍ واحد فقط وعند تكرار ذلك نستطيع معرفة الرَّقم المُختار بخمسة أسئلة فقط في أسوأ الأحوال بدلاً من 30 سؤال .. هذا ما يّدعى بتخفيض التعقيد وهذا تماماً ما يحدث في خوارزميَّات البحث الثنائي😉.
1_2_كسب المعلومات Information Gain
يتمّ حساب هذا المقياس لتحديد أفضل سمة(عمود) لتقسيم البيانات في عقدةٍ ما لتكون هذه السِّمَة الأكثر نقاءً لذا يجب أن يكون مقياس كسب المعلومات لهذه السِّمة(العمود) أكبر من باقي السّمات(الأعمدة) ليتم اختيارها لتقسيم العقدة “أي أنَّ هذه السّمة تعطي أفضل تقسيم للبيانات من غيرها لهذا الفرع”، معادلتها:
Gain(A)=I(s1..sm)-En(A)
حيث: I كميَّة المعلومات الأساسيَّة، (A)E انتروبيَّة السِّمة(العمود)، A السّمة(العمود).
2_التَّقليم Pruning
كما أسلفنا القول بأنَّ طريقة شجرة القرار تأخذ بعين الاعتبار جميع السِّجلات أثناء المُلاءمة، ولهذا السبب فهي عُرضَة للملاءمة الزَّائدة “Overfitting” كون البيانات قد تحتوي ضجيجاً _أي بسبب معالجتها لجميع السّجلات تُصبح دقَّة التَّدريب مرتفعة جداً ولكن عند الاختبار نحصل على خطأ كبير وذلك بسبب أنَّ النَّموذج أصبح مدرَّباً وملاءماً على بيانات التَّدريب فقط_[1]، حيث أنَّ الشَّجرة الأفضل هي ذاتُ الدِّقَّة العالية مع تركيبٍ أبسط وعمقٍ أقل “باختصار عدد عقدٍ أقل مع دقةٍ عالية”، لذا نقوم بعمليَّةِ التَّقليم لتجذيب الشَّجرة وإنقاص العمق، ولها نمطان:
2_1_التَّقليم المسبق Pre_Pruning
يكون مع عمليَّة إنشاء الشَّجرة فيكون إمَّا بتحديد مستوى العمق أي على سبيل المثال نحديد الوصول لأربع مستويات بعد الجَّذر فيتوقَّف بناء الشَّجرة بمجرّد الوصول لذلك العمق لكنَّ هذه الطريقة لا تستخدم كثيراً في التّقليم المسبق لأنَّنا في أغلب الأحيان لا نستطيع تحديد العمق الأنسب للشَّجرة، أمّا الطريقة الأخرى الأكثر استخداماً وهي بتحديد العدد الأعظميّ من السِّجلات في العقدة فيتم تحديد عدد السِّجلات المختلفة في العقدة لإيقاف عمليَّة التَّقسيم، على سبيل المثال لدينا جدول يحوي عدد عيِّنات مقداره 1000 لصنفين A,B من البيانات فيمكننا تحديد سماحٍ لوجود 10 عيِّنات في عقدة الورقة تكون مختلفة عن باقي العيِّنات الموجودة وعندها يتوفق التَّقسيم في هذا الفرع وتصبح هذه العقدة عقدة ورقة للصنف الأكبر الذي تحتويه.
2_2_التَّقليم اللَّاحق Post_Pruning
ويكون بعد عمليَّة إنشاء الشّجرة في حال كانت الشَّجرة ذات عمقٍ كبير أو غير منتهية أو أنَّها دخلت في حالة الملاءمة الزَّائدة، لذا نقوم بتقليل حجمها عن طريق تحويل بعض العقد الفرعيَّة إلى عقد ورقة في حال كانت نسبة الخطأ الَّتي تملكها قليلة ومقبولة ويتم إزالة العقدة الورقيَّة الموجودة أسفل الفرع الأصليِّ وضم سجلاتها مع العقدة الورقة الجديدة.
خطوات الخوارزميَّة
_نحسب كميَّة المعلومات لكاملِ البياناتِ الّتي لدينا بحسب عمود القرار(التَّصنيف).
_نحسب الانتروبيَّة وكسب المعلومات لكل سمة(عمود).
_نأخذ السّمة التي لها أعلى كسبٍ من المعلومات لنقسِّم بحسب واصفاتها ونعتبرها عقدة وواصفاتها هي شروط الانتقال التي تتفرع من العقدة لعقدة أخرى.
_نستمر بما سبق إلى الوصول لعقدةٍ لها انتروبيَّة صفر “جميع سجلاتها من نفس الصِّنف” عندها نتوقف في هذا الفرع عن التَّقسيم.
_تتوقَّف الخوارزميّة عند الوصول إلى شجرة تستطيع تصنيف جميع سجلات البيانات المُعالَجة.
مثال عددي Example
ليكن لدينا البيانات الموضّحة في الجدول في الشَّكل(1):
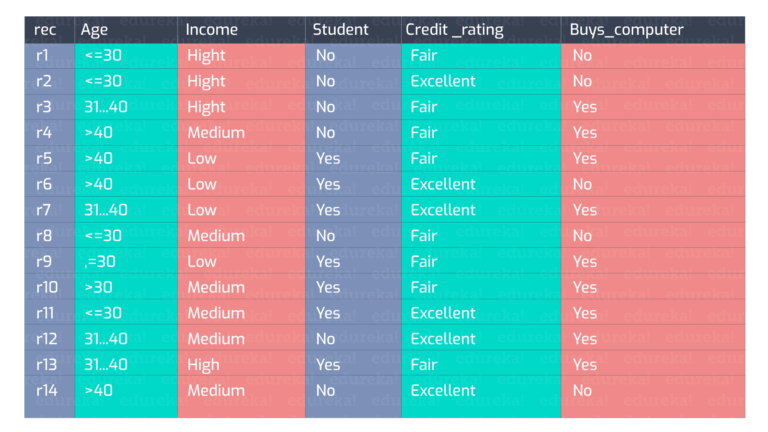
أوَّلاً نقوم بحساب كميَّة المعلومات الأساسيَّة لكامل البيانات حيث لدينا 9 تصنيفات yes من أصل 14 عنصر في الجدول، نوجد احتمال yes:
p(“yes”)=9/14
ولدينا 5 تصنيفات no من أصل 14 عنصر في الجدول،نوجد احتمال no:
p(“no”)=5/14
نحسب كميَّة المعلومات الكليَّة للجدول:
I(9,5)=-(9/14*log2(9/14)+5/14*log2(5/14))=0.94
الآن نحسب مقدار الانتروبيَّة لكل عمود(سمة) من الأعمدة، نبدأ بالعمود age ولدينا ثلاث قيم مميزة(واصفات) لهذا العمود وهي “أصغر من 30، بين 31 و 40، أكبر من 40” وتصنيفاتها في الجدول على الترتيب “2نعم 3لا، 4نعم 0لا، 3نعم 2لا”، فتكون قيمة الانتروبيَّة الخاصَّة بها:
En(“age”)=5/14*I(2,3)+4/14*I(4,0)+5/14*I(3,2)=0.7
ويكون مقدار كسب المعلومات لهذا العمود:
Gain(“age”)=I(9,5)-En(“age”)=0.24
بتكرار تلك العمليَّة على جميع الأعمدة نجد مقدار كسب المعلومات على النَّحو التَّالي:
Gain(“age”)=0.24
Gain(“income”)=0.029
Gain(“student”)=0.151
Gain(“credit_rating”)=0.048
نلاحظ أنَّ مقدار كسب المعلومات للعمود age أكبر من باقي الأعمدة وهذا يدل على أنَّ العمود age هو الأكثر نقاءً بين الأعمدة ويعطي أفضل تقسيم للبيانات ويكون هذا العمود هو العقدة الجَّذر كونه أوَّل عقدة في الشَّجرة كما يظهر بالشَّكل(2):
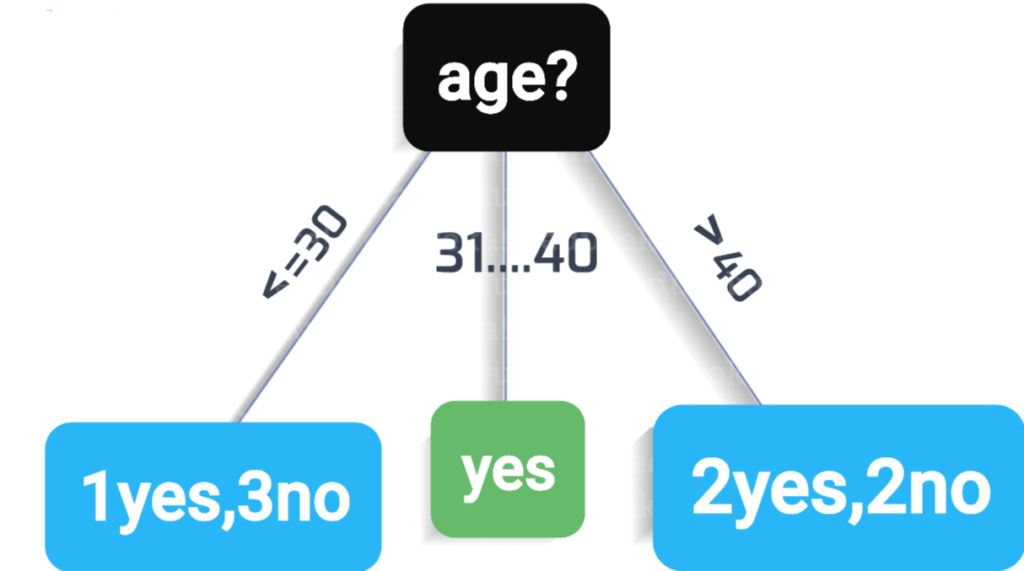
الآن وبعد تجزئة الجدول بحسب واصفات العمود age نلاحظ أنَّ الفرع “بين 30 و 40” يعطينا عقدة تحتوي على سجلات من الصنف yes فقط فتكون هذه القعدة عقدة ورقة ولا يتم تقسيمها بينما في الفرعين الآخرين نلاحظ وجود أكثر من صنف لذا نحتاج إلى تقسيم فنقوم بتكرار الخطوات السابقة على الأعمدة المتبقِّية بعد تجزئة الجدول للحصول على عقد ورقة تعطي تصنيف واحد فقط إمَّا نعم أو لا، كما في الشَّكل(3):
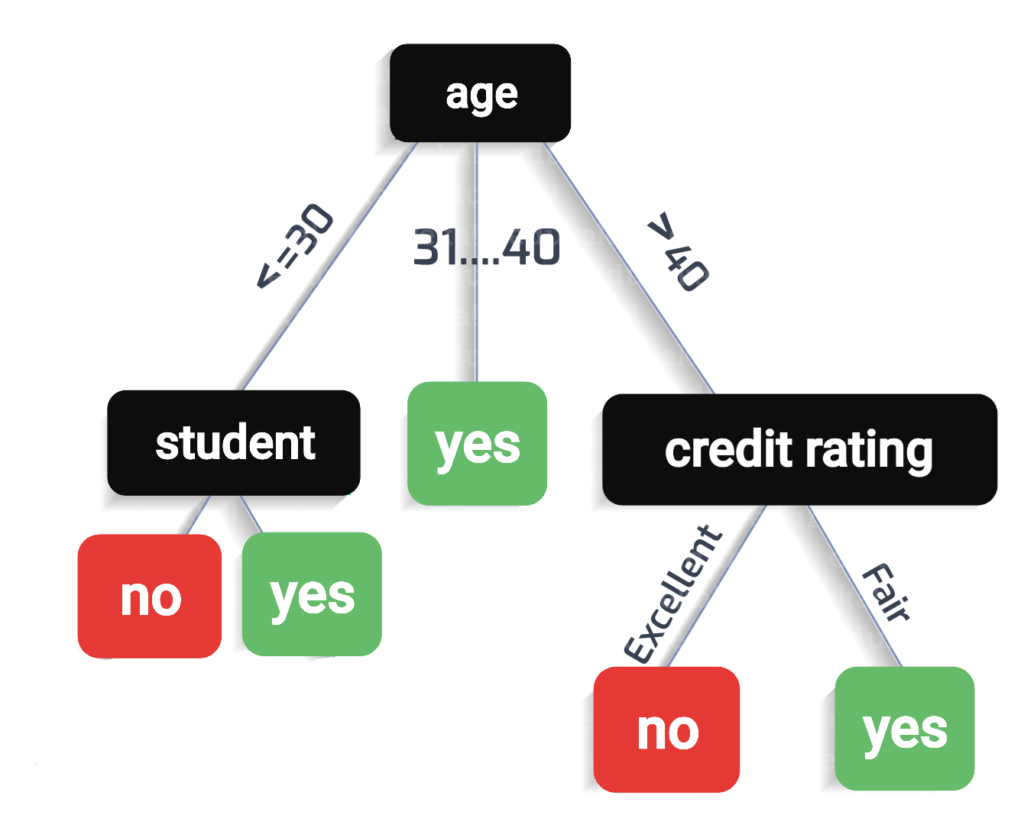
تذكِرة: تتم الحسابات في فروع الشّجرة بحسب الجدول الموجود في العقدة أي بعد تجزئته.
مثال باستخدام لغة البايثون Implementation using Python
سنستخدم ملف بياناتٍ لتصنيف أنواع الزهور تدعى آيريس “IRIS” (هي قاعدة بيانات لثلاث أنواع من الزهور تحوي ميزات يمكن استخلاصها من البيانات لعمليَّة التَّدريب وهي أعمدة لوصف طول السَّبلة وعرضها وأيضاً طول البتلة وعرضها والعمود الأخير للصنف ويحوي اسم الزَّهرة، عدد الأسطر(سجلَّات التَّدريب) 150 سطر وحجم ملف البيانات 3.89 كيلوبايت، وهذه البيانات مشهورة وتطبَّق كثيراً لإختبار خوارزميَّات التَّصنيف)[2]:
_بدايةً نقوم بتضمين المكتبات الأساسيَّة كمكتبة التَّعامل مع المصفوفات نام باي ومكتبة التعامل مع الملفَّات بانداز ومكتبة الرَّسم البياني ماتبلوت ومكتبة اس كي للتَّعلُّم لبناء النموذج.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import sklearn as sk
نقوم بقراءة ملف قاعدة البيانات آيريس باستخدام تابع القراءة raed_csv من مكتبة بانداز.
data = pd.read_csv("iris.csv")
نقوم بعزل البيانات (الأعمدة الأربعة الأولى) عن عمود القرار (العمود الخامس) لتكون بيانات دخلٍ لعمليَّة التَّدريب.
x = data.iloc[:,:4]
نقوم بعزل عمود القرار ليتم مقارنته مع نتيجة التَّدريب.
y = data.iloc[:,4:]
نستخدم المكتبة اس كي للتَّعلُّم ونستدعي التابع train_test_split لتقسيم البيانات بنسبة ثمانون بالمئة للتدريب وعشرون بالمئة للاختبار.
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x,y,test_size = 0.2,random_state = 42)
نقوم ببناء قالب النّموذج من خلال تضمين النَّموذج DecisionTreeClaSsifier من مكتبة اس كي للتَّعلُّم قسم الشَّجرة وإنشاء كائن منها وسيحتوي على توابع وعمليَّات التَّصنيف.
from sklearn.tree import DecisionTreeClassifier
dec_tree = DecisionTreeClassifier()
نستخدم التَّابع fit لملاءمة النَّموذج.
dec_tree.fit(x_train,y_train)
نستخدم التَّابع score لحساب دقِّة النَّموذج ومن ثمَّ نقوم بإظهارها.
print("Decision Tree Classification Score: ",dec_tree.score(x_test,y_test))
نستخدم التّابع plot_tree لرسم الشّجرة النِّهائيَّة للنَّموذج وثمّ نقوم بإظهارها.
sk.tree.plot_tree(dec_tree)
plt.show()
ناتج الدِّقَّة:
Decision Tree Classification Score: 1.0
نلاحظ أنَّ الدِّقَّة كاملة بسبب أنَّ البيانات الَّتي اختبرنا عليها بسيطة وصغيرة بعض الشَّيء.
الشّجرة النِّهائيَّة ممثَّلة بالشَّكل(4):
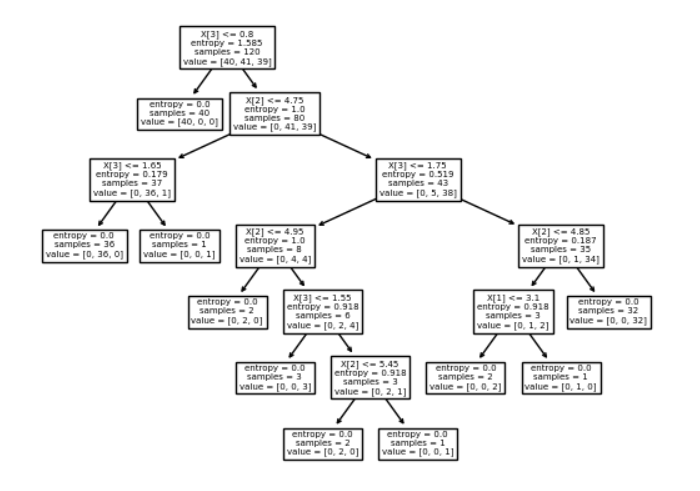
تمثيل ما سبق بشكلٍ بيانيٍّ لإظهار التّقسيم في كل مستوى يظهر في الأشكال التَّالية:
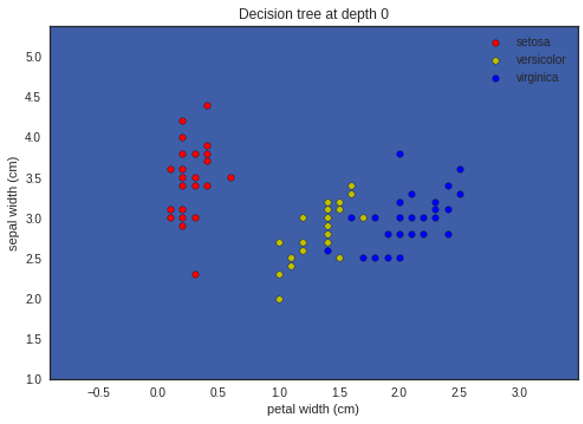
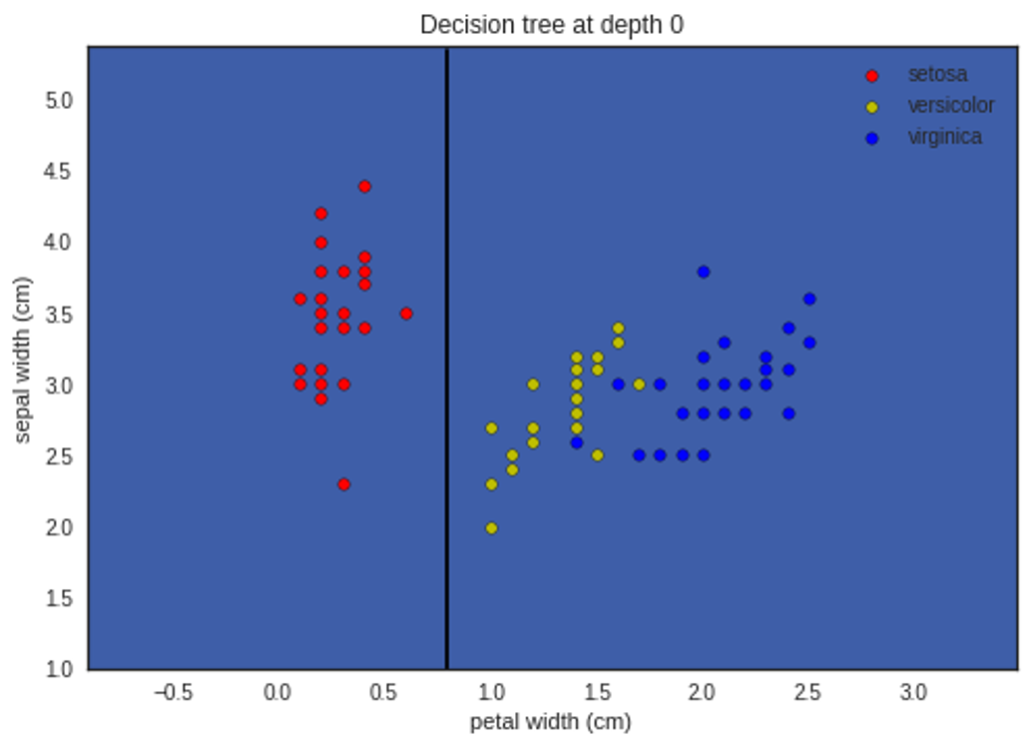
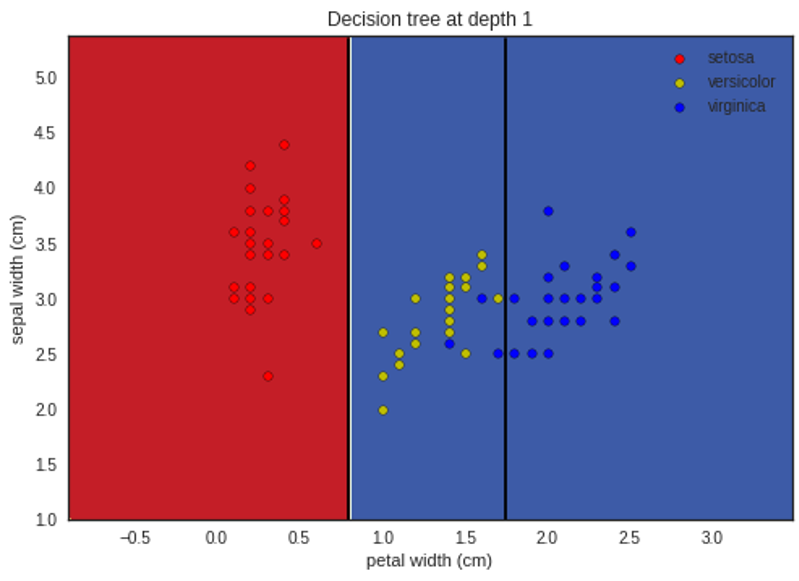
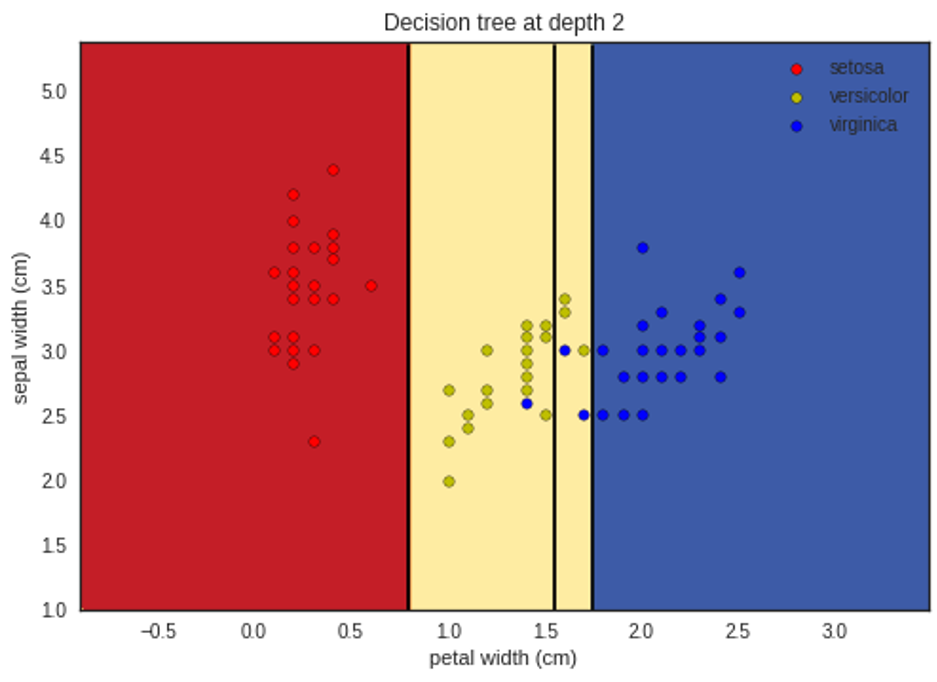
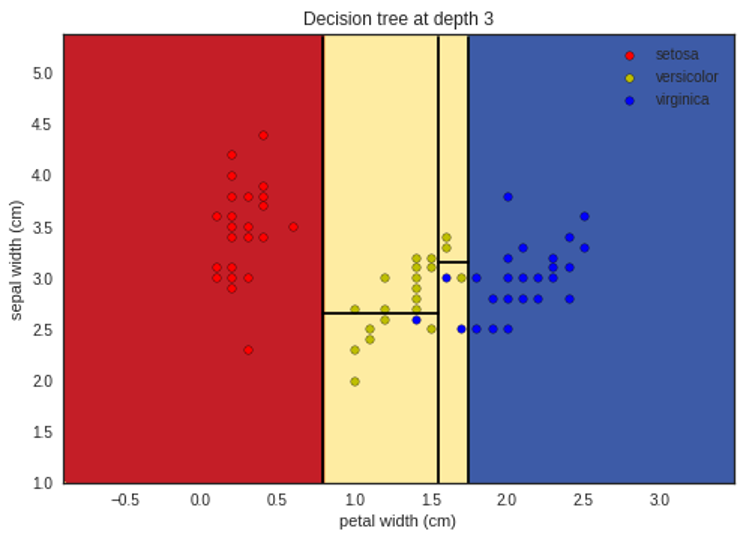
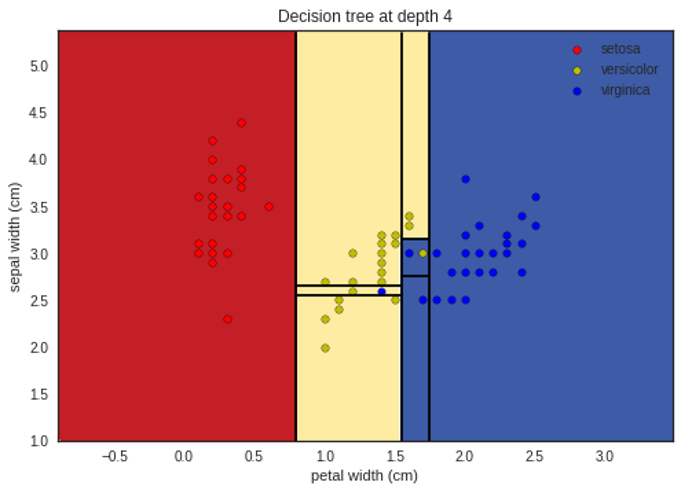
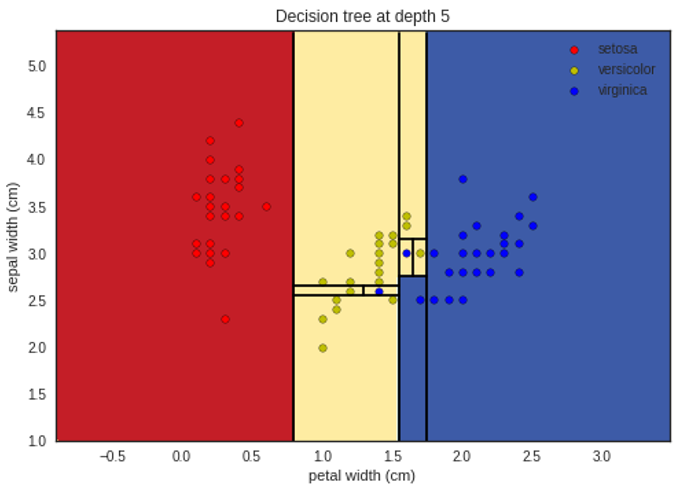
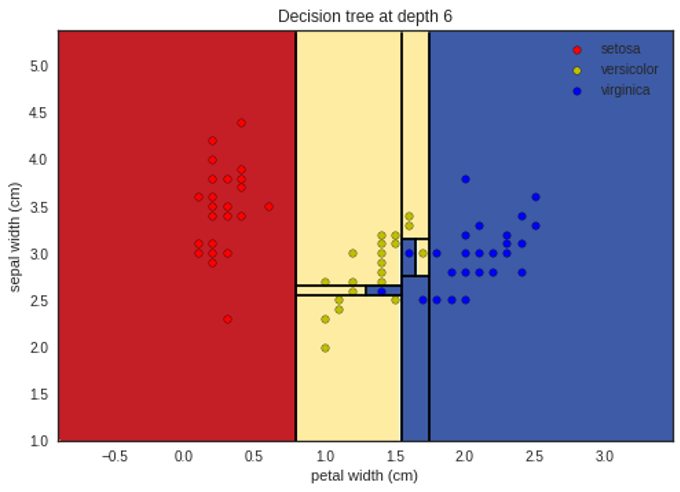
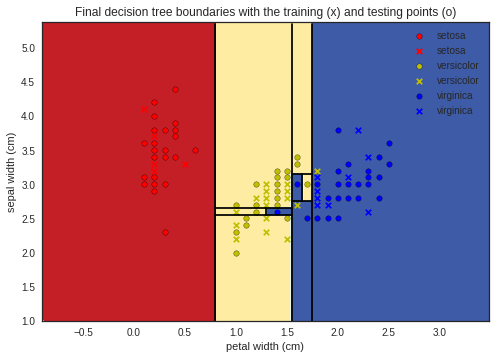
لمتابعة الشفرة البرمجية للمثال بلغة البايثون يمكنكم زيارة مستوع الغيت هب الخاص بمدونة الذكاء الاصطناعي باللغة العربية.
الإيجابيَّات
إنَّ أشجار القرار سهلة الفهم والتَّنفيذ لأنها لا تحتوي على معاملات بل تعتمد على تقسيم البيانات في كلِّ عقدةٍ حتى الوصول لعقدةٍ نقيةٍ(تحوي بيانات من صنف واحد) وتكون هذه عقدة ورقة.
_تُستخدم أشجار القرار في تحديد القرار سواءٌ كانت لعمليّة تصنيف أو انحدار، حيث إنَّ عمليَّة السير ضمن الشَّجرة تُشبِه عمليَّة تكرارٍ لأسئلةٍ للوصول إلى النَّاتج(القرار).
_تعمل أشجار القرار مع البيانات الفئويَّة والرقميَّة، أي يمكن تنفيذها في حال كانت البيانات اسميَّة أو رقميَّة.
السَّلبيَّات
_كثيراً ما تَدخُل خوارزميَّات أشجار القرار في حالة الملاءمة الزَّائدة بسبب معالجتها لجميع سجلَّات البيانات وقد يكون بعضها عبارة عن بياناتٍ خاطئةٍ أو مشوَّشة فيتم معالجتها كأنَّها بيانات طبيعيَّة بدلاً من تجاهلها.
الخُلاصة
أشجار القرار أحد طرق تعلُّم الآلة من نوع التَّعلُّم بإشراف، وهي تستخدم غي مشاكل التصنيف والانحدار حيث لها عدَّة خوارزميَّات مثل: ID3 و C4.5 وغيرها لكنَّ جميعها تعتمد على نفس المبدأ.
المراجع
[1] Decision Trees Explained Easily
[2] Understanding Decision Trees
[3] Understanding Decision Trees in Machine learning
[4] Shanon entropy