المقدّمة Introduction:
في حال كانت لديك بيانات وطُلب مِنك نمذجتُها بطريقة الانحدار، ماهي أوَّل خوارزميةٍ لتعلُّم الآلة ستقوم بتنفيذِها؟! الإجابة _هي عادةً_ الانحدار الخطي لمعظمنا (بما فيهم أنا) لأنَّها أبسطهم وأسهلهم تنفيذاً، ولكن ماذا لو كان نموذجُ الانحدار الخطّيّ لا يستطيع نمذجةَ العلاقةِ بين المتغيِّر التَّابع والمتغيِّر المستقل؟ أو بمعنًى آخر، ماذا لو لم تكن هنالك علاقةٌ خطِّيَّةٌ بينهما؟ حينها سنستخدم النَّماذج الغير خطِّيَّة لملاءمة البيانات، ومنها نموذجُ الانحدار متعدِّد الحدود ..
الفرقُ بين الانحدار الخطّيّ والانحدار متعدّد الحدود
Polynomial Regression vs. Linear Regression
الانحدارُ متعدّد الحدود هو علاقةٌ خاصةٌ من الانحدار الخطّيّ، حيث يتمّ نمذجة البيانات بعلاقةٍ منحنيةٍ بين المتغيِّر التَّابع والمتغيِّر المستقل، بينما الانحدار الخطّيّ يُستخدَم للعلاقات الخطّيّة فقط[1].
في الانحدار الخطّيّ وباستخدام متغيِّرٍ مستقلٍ واحد، تكون العلاقةُ بالشّكل التّالي:
ϒ=β1.χ1+β0
حيث:ϒ المتغيّر التّابع، χ المتغيّر المستقلّ، β0 قيمة الانحياز (هي قيمة ϒ في حال كانت قيمة χ صفر)، β1 الوزن المرتبط بχ.
يمكننا استخدام هذه المعادلة الخطّيّة لتمثيل علاقةٍ خطّيّةٍ بين المتغيّر التّابع والمتغيّر المستقل، أمَّا في الانحدار متعدّد الحدود لدينا معادلةٌ متعدِّدة الحدود من الدّرجة n مُمثَّلةٌ على النّحو التّالي:
ϒi=∑βi.χi^n+β0
حيث:ϒ المتغيّر التّابع، χ المتغيّر المستقل، β0 قيمة الانحياز (هي قيمة ϒ في حال كانت قيمة χ صفر)، ¡β حيث i=1…n الأوزان المرتبطة بχ، وn هي درجةُ كثير الحدود.
ملاحظة: كلَّما زادت قيمةُ n زادت درجةُ كثير الحدود وبالتّالي تصبح المعادلة أكثرَ تعقيداً.
الآن وبعد أن أصبح لدينا فهمٌ أساسيٌ للانحدار الخطّيّ والانحدار متعدّد الحدود، سنقوم بتنفيذ مثالٍ بلغة البايثون على مجموعةِ بياناتٍ بسيطةٍ بحيث يكون لدينا علاقةٌ منحنيةٌ بين المتغيّر التّابع والمتغيّر المستقل، وسنستخدم كليهما ونقارنُ بين النتائج لفهم الفرقِ بين الاثنين.
المثال العمليّ باستخدام لغة البايثون مع الشرح
في البداية سنقوم باستيراد المكتباتِ المطلوبة، ونقوم برسم كلٍّ من المتغيِّر التّابع والمتغيِّر المستقل:
#تضمينُ المكاتب (مكتبة البايثون العدديّة و الرّسم الرياضيّ)
import numpy as np
import matplotlib.pypolt as plt
#تضمينُ حزمة المصفوفات من مكتبة إس كي تعلّم للتّمكّن من حساب الخطأ بطريقة آر إم إس إي (جذر متوسط مربع الخطأ)
Import sklearn.metrics as skm
#تشكيلُ بياناتٍ ذات ارتباط غير خطيّ
x=10*np.random.normal(0,1,70)
y=10*(-x**2)+np.random.normal(-100,100,70)
#رسم البيانات على المستوي
plt.figure(figsize=(10,5))
plt.scatter(x,y,s=15)
plt.xlabel(‘Predicator’,fontsize=16)
plt.ylabel(‘Target’,fontsize=16)
plt.show()
شرح أسطر الكود السّابق:
الأسطر 1,4,6,9 الإشارة # تعني تعليق للسّطر.
2_تضمين مكتبة البايثون العدديّة نام باي (numpy) للتّعامل مع المصفوفات والعمليّات الحسابيّة السّريعة عليها[2]، وas لاستخدام np بدلاً من الاسم الأصليّ.
3_تضمينُ مكتبة الرّسم الرّياضي ماتبلوت (matplotlib) وهي مكتبة رسوميّة من الماتلاب (للرسم البيانيّ)[3]، وأيضاً استبدال للاسم بplt.
5_تضمينّ مكتبة اس كي للتعلّم وهي المكتبة الأضخم لمعارف تعلّم الآلة[4] قسم المصفوفات لحساب الخطأ بطريقة آر إم إس إي، وأيضاً استبدالٌ للاسم بskm.
7_إنشاءُ مصفوفةٍ أحاديّةٍ من الأرقام العشوائيّة، تحوي 70 رقماً عشوائيّاً محسوباً بطريقة التّوزيع الغوصيّ حيث 1 هو الانحراف المعياريّ، و0 متوسّط مركز التّوزيع “أي تكون كثافةُ النقاط عند الصّفر”.
8_إنشاءُ مصفوفةٍ أحاديّةٍ من الأرقام العشوائيّة، تحوي 70 رقماً عشوائيّاً محسوباً بطريقة التّوزيع الغوصيّ حيث 100 هو الانحراف المعياريّ، و100- متوسّط مركز التّوزيع “أي تكون كثافةُ النقاط عند 100-“.
10_رسمُ مستوٍ بيانيّ بأبعاد 10 أفقي، 5 عمودي.
11_رسمُ النّقاط باعتبار كلِّ نقطةٍ هي تقاطع الزّوج المتقابل من المصفوفتين x,y، وحجم كلِّ نقطة 15 بكسل.
12_كتابةُ “predicator” لتوصيف المحور x.
13_كتابةُ “target” لتوصيف المحور y.
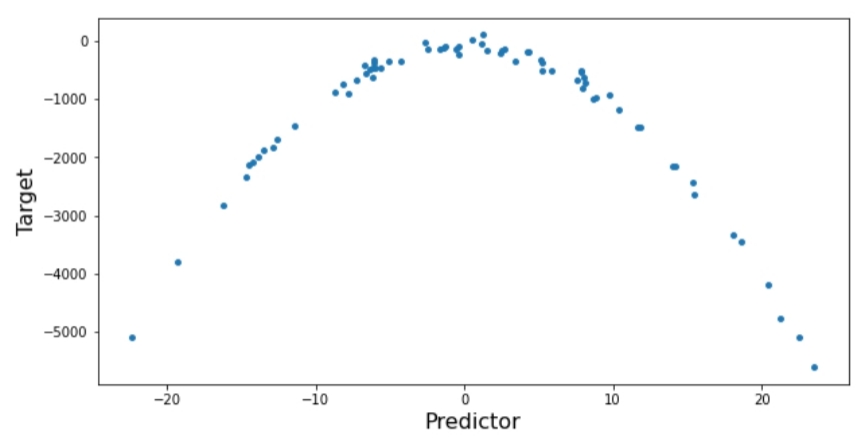
14_إظهارُ ماسبق.
ويظهر لدينا الشّكل(1) التّالي:
الآن لنقوم بتنفيذ الانحدار الخطّيّ على النّموذج:
#تضمين لنموذج الانحدار الخطيّ من خلال مكتبة إس كي للتعلّم
import sklearn.linear_model as skl
#تدريبُ النّموذج
lm=skl.LinearRegression()
lm.fit(x.reshape(-1,1),y.reshape(-1,1))
y_pred=lm.predict(x.reshape(-1,1))
#رسمُ المعادلة النّاتجة عن التّدريب
plt.figure(figsize=(10,5))
plt.scatter(x,y,s=15)
plt.plot(x,y_pred,color=’r’)
plt.xlabel(‘Predicator’,fontsize=16)
plt.ylabel(‘Target’,fontsize=16)
plt.show()
شرح أسطر الكود السّابق:
2_تضمين مكتبة اس كي للتعلّم حزمة الانحدار الخطّيّ، وأيضاً استبدالّ للاسم بskl.
4_إنشاءُ الكائن lm الّذي يحوي تابعَ الانحدار الخطّيّ واستخدامه لملاءمةِ البيانات.
5_إحضارُ نسخةٍ من المصفوفتين x,y ولكن بشكلِ عمودٍ واحدٍ، وملاءمة البيانات “تدريبها واستنتاج معادلة لها”.
6_إجراءُ تنبّؤاتٍ حول حالات الاختبار (المتغيّر المستقل) وحفظ تلك النقاط.
10_رسمُ الخط المُمَثِّل لأفضلِ ملاءمة ممكنة باستخدام الانحدارِ الخطّيّ.
ويظهر لدينا الشّكل(2) التّالي:
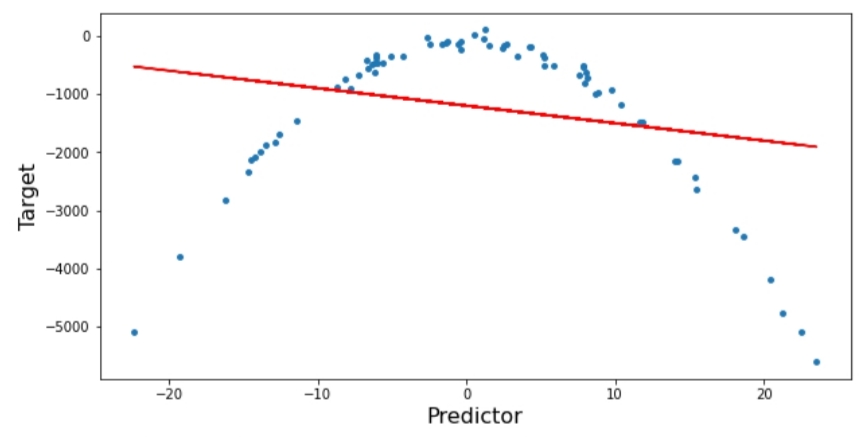
نقومُ بحساب نسبة الخطأ (جذر متوسط مربع الخطأ RMSE) على النّحو التّالي:
print(‘RMSE for Linear Regression =>’,np.sqrt(skm.mean_squared_error(y,y_pred)))
تقوم العمليّة آر إم إس إي على متوسّط مجموعِ مربعات الفروقات بين القيم الأساسيّة والقيم المُتَنَبَّأَة.
ويظهر النّاتج كالتّالي:
RMSE for Linear Regression=> 1339.7026
يمكننا أن نُلاحظ بوضوح أنَّ نموذج الانحدار الخطّيّ غيرُ قادرٍ على ملاءمة البيانات بشكلٍ صحيح، وأنَّ نسبةَ الخطأ آر إم إس إي مرتفعةٌ جداً.
سنقوم الآن بتجربة الانحدار متعدّد الحدود، وتنفيذُه يحتاج إلى عمليّة تدعى مسار التّدفّق (Pipeline) من مكتبة اس كي للتعلّم وهي مكوّنة من خطوتَين:
أوّلاً: نقومُ بتمثيل البيانات بكثيرِ حدود باستخدام العلاقة PolynomialFeatures من مكتبة اس كي للتعلّم.
ثانياً: نستخدمُ الانحدار الخطّيّ لملاءمة البيانات.
حيث مسار تدفّق البيانات Pipeline يأخذ البياناتِ ويعطي علاقة التنبُّؤ، وضمن هذه العمليّة تمرّ البياناتُ بالخطوتَين السابقتَين.
#تضمينُ حزمة استخلاص الميّزات من مكتبة إس كي تعلّم لإنشاء نموذج انحدار متعدّد الحدود
import sklearn.preprocessing as skp
#تضمينُ حزمة مسار تدفّق البيانات من مكتبة إس كي تعلّم
import sklearn.pipeline as skpip
#إنشاءُ مسار تدفّق البيانات وملاءمتها
Input=[(‘polynomial’,skp.PolynomailFeatures(degree=2)),(‘modal’,skl.LinearRegression())]
pipe=skpip.Pipeline(Input)
pipe.fit(x.reshape(-1,1),y.reshape(-1,1))
شرح أسطر الكود السّابق:
2_تضمين مكتبة اس كي للتعلّم حزمة preprocessing لاستخلاص الميِّزات.
4_تضمين مكتبة اس كي للتعلّم حزمة Pipeline لتجميع عدَّةِ خطواتٍ معاً.
6_إنشاءُ متحوّلٍ يحوي كثير حدودٍ من الدّرجة الثّانية، ونموذج انحدارٍ خطّيّ لتطبيق الانحدار متعدّد الحدود.
7_إنشاءُ متحوّلٍ يحوي ماسبق ضمن خطِّ عمليّات مغلق.
8_تفعيلُ ملاءمة البيانات.
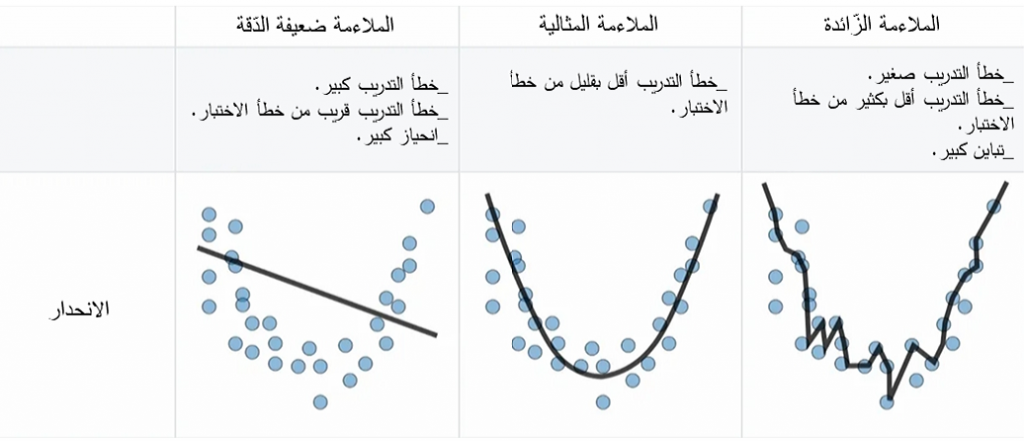
ملاحظة: يمكننا اختيار درجةِ كثير الحدود بناءً على العلاقة بين المتغيّر التّابع والمتغيّر المستقل، لاحظ أنَّه في حال كان كثيرُ الحدود من الدّرجة الأولى يصبح انحداراً خطّيّاً بسيطاً، وفي حال ازدادت درجةُ كثير الحدود يزداد معه تعقيد النّموذج، لذلك يجب تحديد قيمة n بدقَّة، فإذا كانت هذه القيمةُ منخفضة فلن يكون النّموذجُ قادراً على ملاءمة البيانات بالشّكل الصحيح، وهذا ما يُعرف بالملاءمة ضعيفةِ الدّقة “underfitting”، وإذا كانت عاليةً تصبح الملاءمةُ زائدةً عن الحدّ “تصل لنقطة لا يصبح هنالك جدوى من الملاءمة أكثر من ذلك وتصبح نسبة خطأ الإختبار كبيرة كون النّموذج أصبح مدرباً فقط لبيانات التّدريب”، وهذا ما يّعرف بالملاءمة الزّائدة “overfitting” والشّكل(3) يوضّح ذلك.
poly_pred=pipe.predict(x.reshape(-1,1))
#ترتيبُ القيم المُتنبّأة
sorted_zip=sorted(zip(x,poly_pred))
x_poly,pol_pred=zip(*sorted_zip)
#رسمُ المعادلات النّاتجة عن التّدريب
plt.figure(figsize=(10,5))
plt.scatter(x,y,s=15)
plt.plot(x,y_pred,color=’r’,label=’Linear Regression’)
plt.plot(x_pred,pol_pred,color=’g’,label=’polynomial Regression’)
plt.xlabel(‘Predicator’,fontsize=16)
plt.ylabel(‘Target’,fontsize=16)
plt.legend()
plt.show()
شرح أسطر الكود السّابق:
1_إيجادُ قيم التنبّؤ بعد الملاءمة.
3_القيامُ بفرزِ وترتيب العناصر المتقابلة.
4_توزيعُ العناصر المرتّبة إلى مصفوفتَين منفصلتَين.
12_لوضع المسمَّيات والإيضاحات ضمن مستوعبٍ جانبيّ.
وتظهر النّتيجة بالشّكل(4) التّالي:
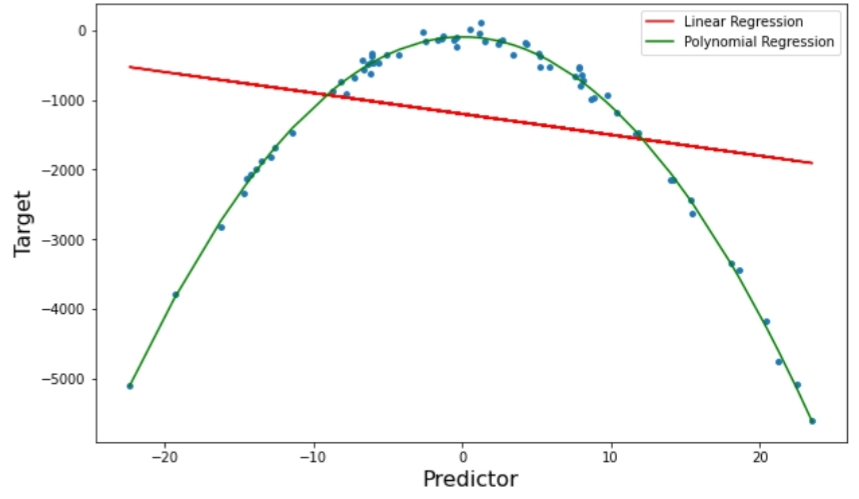
نقوم بحسابِ نسبة الخطأ على النّحو التّالي:
print(‘RMSE for Polynomial Regression =>’,np.sqrt(skm.mean_squared_error(y,poly_pred)))
ويظهر النّاتج كالتّالي:
RMSE for Polynomial Regression=> 88.5037
عزيزي القارئ يمكنك قراءة كامل الشفرة البرمجية على موقع الغيت هاب هنا.
الخاتمة:
من خلال النّتائج السّابقة المبيّنة في الشّكل(4) وقيمة آر إم إس إي للانحدار متعدّد الحدود والانحدار الخطّيّ، يمكننا أن نلاحظ بوضوحٍ أنَّ الانحدارَ متعدّد الحدود أفضلُ لملاءمة البيانات السّابقة من الانحدار الخطّيّ؛ كونها بياناتٌ ذات علاقةٍ منحنيةٍ بين المتغيِّر التّابع والمتغيّر المستقل.
في حال رغبتَ في التّعرّف على أنواعٍ أخرى من نماذجِ الانحدار يمكنك قراءة مقال “الانحدار“.
المراجع:
2_ Numpy
3_ Matplotlib
4_ Scikit_Learn