- المقدّمة
- التعلّم العميق
- طريقة تحليل العنصر الأساسيّ (PCA)
- تعريف العناصر الأساسيّة
- المفهوم الرّياضيّ لطريقة تحليل العنصر الرئيسيّ
- مجموعة بيانات سرطان الثديّ وتحليل العنصر الأساسيّ
- مجموعه بيانات CIFAR – 10
- النموذج المتسلسل Sequential model
- الخاتمة
- المراجع
المقدّمة
سوف نتناول في هذه المقالة تعريف تحليل العنصر الرئيسيّ، وسوف يتمّ تنفيذ الأمثلة باستخدام مكتبات بايثون، وذلك من خلال طريقة تعلّم اختيار الميّزات واستخراجها عند بناء نماذج التعلم الآليّ والتعلم العميق. إنّ طريقة تحليل العنصر الأساسيّ تعتبر واحدةً من الطرق المهمة المستخدمة في تعلّم الآلة، وهي طريقة لتقليل الأبعاد (Dimensions) تستخدم غالبًا لتقليل أبعاد مجموعات البيانات الكبيرة، عن طريق تحويل مجموعة كبيرة من المتغيّرات إلى مجموعة أصغر لا تزال تحتوي على معظم المعلومات الهامّة في المجموعة الكبيرة.
عند استخدام طريقة تحليل العنصر الرئيسيّ، نحاول الحفاظ على الأجزاء الأساسيّة التي تحتوي على مزيد من التباين في البيانات، وإزالة الأجزاء غير الأساسيّة مع تباينٍ أقلّ.
إنّ الأبعاد ليست سوى ميّزات تمثل البيانات، على سبيل المثال تحتوي صورة (28 × 28) على 784 عنصرًا وهي عبارة عن الأبعاد أو الميزات (features) التي تمثل معًا تلك الصورة.
التعلّم العميق Deep learning
هو مجال بحثيّ جديد يتناول إيجاد نظريّات وخوارزميّات تتيح للآلة أن تتعلّم بنفسها؛ عن طريق محاكاة الخلايا العصبيّة في جسم الإنسان. سنتعرّف من خلال هذه المقالة على كيفيّة تسريع عمليّة تدريب نموذج التعلّم العميق باستخدام تحليل العنصر الأساسيّ.
طريقة تحليل العنصر الأساسيّ
هي عبارة عن إجراء إحصائيّ يستخدم تحويلًا متعامدًا؛ لتحويل مجموعة من المتغيّرات المرتبطة إلى مجموعة من المتغيّرات غير المرتبطة خطيًّا تسمى العناصر الأساسيّة.
تعريف لاعناصر الأساسية
العناصر الأساسيّة تمثل المفتاح الأساسيّ لطريقة تحليل العنصر الأساسيّ، فهي تمثل المعلومات الأساسيّة للبيانات عند استخدام محرّكات البحث فيها، وذلك عندما يتمّ إسقاط البيانات في بُعد أقلّ (مثلًا ثلاثة أبعاد) من مساحة أعلى. إنّ الأبعاد الثلاثة ليست سوى العناصر الأساسيّة الثلاثة التي تحتفظ بمعظم التباين لتلك البيانات.
نلاحظ أنّ تقليل عدد متغيّرات مجموعة البيانات الكبيرة يؤثر على حساب الدّقة، ولكنّ الحيلة في تقليل الأبعاد تكمن في مبادلة القليل من الدّقة لتقليل البيانات، لأنّ مجموعات البيانات الأصغر يسهل استكشافها وتصوّرها، وتجعل تحليل البيانات أسهل بكثير وأسرع عند استخدام خوارزميّات التعلم الآليّ أو التعلّم العميق بدون الحاجة لمتغيّرات خارجيّة للمعالجة. ويمكن القول باختصار: إنّ فكرة تحليل العنصر الأساسيّ بسيطة وتكمن الفكرة الأساسيّة في تقليل عدد متغيّرات مجموعة البيانات، مع الحفاظ على أكبر قدْر ممكن من المعلومات.
المفهوم الرّياضيّ لطريقة تحليل العنصر الرئيسيّ
من المهمّ بالنسبة لنا أن ندرس المفاهيم الرّياضيّة الكامنة وراء استخدام طريقة تحليل العنصر الأساسيّ، من أجل فهمٍ أفضل لهذه الطريقة و لتساعدنا هذه المفاهيم في تحديد المكوّنات\العناصر الأساسيّة لمجموعة بيانات معيّنة. تستخدم هذه الطريقة المفاهيم الثلاثة التالية: مصفوفة التّغاير Covariance matrix، المتجهات الذّاتية Eigenvector والقيم الذّاتية Eigenvalues، لتنفيذ طريقة تحليل العنصر الأساسيّ، مما يوفر مجموعة من المتجهات الذّاتية والقيم الذّاتية الخاصة بها.
الآن عزيزي القارئ سوف نتعرّف على مصفوفة التّغاير وكيف تساعدنا في حساب المكوّنات\العناصر الأساسيّة. إنّ مصفوفة التّغاير هي عبارة عن مقياس “انتشار” مجموعة من النقاط حول مركز كتلتها (الوسط).
يتمّ قياس التباين\التغاير بين بُعدين لمعرفة ما إذا كانت هناك علاقة بين البُعدين، على سبيل المثال عدد ساعات الدّراسة والعلامات التي تمّ الحصول عليها.
المعادلة التالية رقم (1) هي الصيغة الرّياضيّة لحساب مصفوفة التّغاير
X,Y تمثل المتغيّرات في المصفوفة، و i يمثل عدد صفوف المصفوفة وهي مصفوفة مربّعة حيث عدد الصفوف يساوي عدد الأعمدة.
مصفوفة التّغاير هي مصفوفة مربّعة لأنّ التّغاير بين X و Y هو نفسه بين Y و X، لذلك فإنّ التغاير المشترك لكلّ زوج من المتغيّرات يتمّ عرضه مرّتين في المصفوفة، ونتيجةً لذلك فإنّ التّغاير المشترك بين المتغيّرين i و j يكون في الموضعين (i، j) و (j، i).
العيّنة(sample) هي مجموعة فرعيّة (مجموعة أصغر) من المجموعة المستهدفة\الكبيرة (Population). وكلّ دراسة لها استفسار، ومن أجل الإجابة عليه يتمّ أخذ عيّنة من المجموعة المستهدفة ودراستها، من المفترض أن تكون العيّنة ممثِّلة لكامل المجموعة وتهدف إلى استخلاص رؤى عنها. يجب استخدام العيّنات لأنه في كثير من الأحيان يكون من الصعب للغاية دراسة المجموعة المستهدَفة بأكملها.
الآن عزيزي القارئ سوف نعمل على تطبيق طريقة تحليل العناصر الأساسيّة على نوعين من البيانات؛ بيانات نصيّة باستخدام مجموعة قاعدة بيانات سرطان الثديّ، ومن ثمّ سوف نستخدم بيانات صوريّة ممثّلة في مجموعة بيانات CIFAR-10 (المعهد الكنديّ للأبحاث المتقدّمة)، وهي أيضاً موجودة في بايثون، وفيما يلي سوف نقوم بعمل شرحٍ مبسّط لمحتوى البيانات في كلّ مجموعة.
مجموعة بيانات سرطان الثديّ
مجموعة بيانات سرطان الثديّ هي بيانات متعدّدة المتغيرات ذات قيم عدديّة حقيقيّة تتكوّن من فئتين، حيث تشير كلّ فئة إلى احتمال إصابة المريض بسرطان الثديّ أم لا، الفئتان هما: الخبيثة والحميدة.
تحتوي مجموعة البيانات على 569 عيّنة مقسمة إلى فئتين؛ تحتوي الفئة الأولى الخبيثة على 212 عيّنة، بينما تحتوي الفئة الثانية الحميدة على 357 عيّنة.
تحتوي على 30 خاصيّة مشتركة في جميع الفئات: نصف القطر، الملمس، المحيط، المساحة، النعومة، البعد الكسوريّ، إلخ.
سنقوم باستيراد مجموعة بيانات سرطان الثديّ بالإضافة إلى كلٍّ من التسميات وجلب البيانات، ولعمل ذلك سنقوم باستدعاء الدّالة data، ولجلب التسميات (أسماء الأصناف) سوف نستخدم الدّالة target.وذلك من خلال الشفرة البرمجيّة التالية:
from sklearn.datasets import load_breast_cancer
breast = load_breast_cancer()
breast_data = breast.data
breast_labels = breast.target
الآن سوف نتحقق من شكل البيانات الموجودة باستخدام الدّالة shape
breast_data.shape
سوف نلاحظ من خلال المخرجات، أنّ مجموعة البيانات هذه تحتوي على 569 عيّنة موصوفة باستخدام 30 خاصيّة لهذه البيانات
(569, 30)
سنقوم الآن باستيراد مكتبة بايثون العدديَّة numpy، نظرًا لأننا سنعيد تشكيل التّسميات breast_labels لكي نتمكن من ربطها بالبيانات breast_data لننشئ أخيرًا إطارًا يحتوي على كلٍّ من البيانات والتسميات مع بعضها لتسهيل التعامل معها لاحقًا.
import numpy as np
labels = np.reshape(breast_labels,(569,1))
بعد إعادة تشكيل التسميات سنقوم بربط البيانات والتسميات على طول المحور الثاني، مما يعني أنّ الشكل النهائيّ للبيانات سيكون 569 × 31.
final_breast_data = np.concatenate([breast_data,labels],axis=1)
final_breast_data.shape
output
(569, 31)
سنقوم الآن باستيراد مكتبة تحليل البيانات في بايثون pandas لتمثيل البيانات على شكل جدول
import pandas as pd
breast_dataset = pd.DataFrame(final_breast_data)
في السطر التالي سوف نتعرّف على المتغيّرات (المميزات) في مجموعة بيانات سرطان الثديّ، سوف تلاحظ عزيزي القارئ 30 متغيرًا أو خاصيّة لتلك البيانات كما في المخرجات
features = breast.feature_names
features
output
array(['mean radius', 'mean texture', 'mean perimeter', 'mean area',
'mean smoothness', 'mean compactness', 'mean concavity',
'mean concave points', 'mean symmetry', 'mean fractal dimension',
'radius error', 'texture error', 'perimeter error', 'area error',
'smoothness error', 'compactness error', 'concavity error',
'concave points error', 'symmetry error',
'fractal dimension error', 'worst radius', 'worst texture',
'worst perimeter', 'worst area', 'worst smoothness',
'worst compactness', 'worst concavity', 'worst concave points',
'worst symmetry', 'worst fractal dimension'], dtype='<U23')
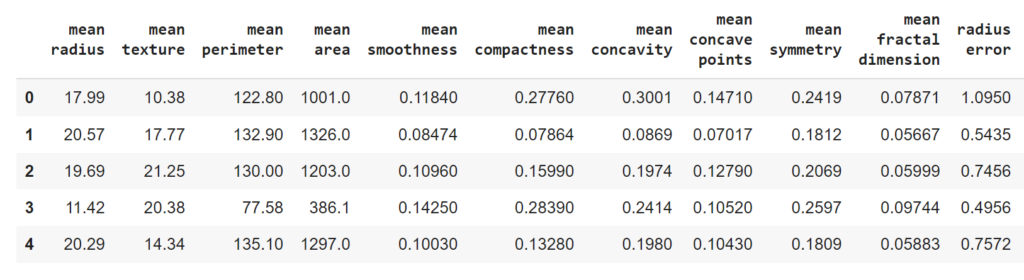
سوف نقوم بإضافة حقل التسميات إلى مصفوفة البيانات، ومن ثمّ نستعرض السطور الأولى من البيانات باستخدام الدّالة head وتكون النتيجة النهائيّة كما في الشكل (1).
features_labels = np.append(features,'label')
breast_dataset.columns = features_labels
breast_dataset.head()
من المتعارف عليه إجراء عمليّة تقييس Normalization للبيانات قبل تطبيق أيّ خوارزميّة لتعلّم الآلة، لذلك قبل استخدام طريقة تحليل العناصر الأساسيّة سوف نقوم بعمليّة توحيد Standardization المتغيّرات المستمرّة لمجموعة البيانات. ولإجراء عمليّة التوحيد سوف نستورد الفئة StandardScaler من المكتبة sklearn ومن ثمّ نقوم باختيار المتغيرات، ثم نقوم بتطبيق عمليّات القياس scale مستخدمين الدّالة fit_transform على جميع المتغيّرات، أثناء تطبيق StandardScaler يجب توزيع كلّ متغير من البيانات بشكل طبيعيّ، بحيث يتمّ قياس التوزيع إلى متوسطٍ صفر وانحراف معياريّ بمقدار واحد.
from sklearn.preprocessing import StandardScaler
x = breast_dataset.loc[:, features].values
x = StandardScaler().fit_transform(x)
np.mean(x),np.std(x)
output
(-6.118909323768877e-16, 1.0)
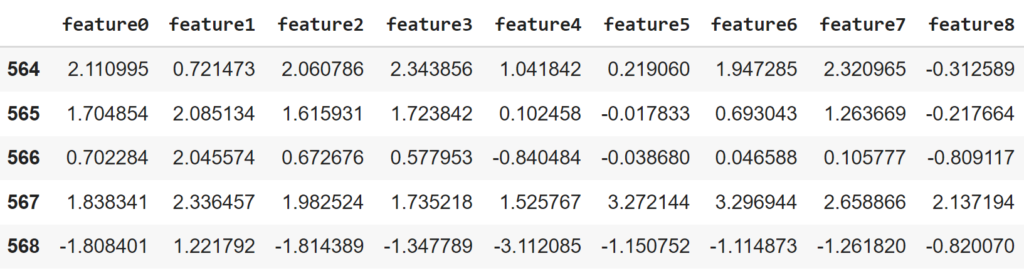
الآن سنقوم برؤية المتغيّرات الجديدة بعد تقييس Normalization على شكل جدول باستخدام الدّالة dataframe، واستعراض بعض الصفوف الأخيرة من مجموعة البيانات باستخدام الدّالة tail. الشكل (2) يوضح شكل البيانات بعد عمليّة التقييس.
feat_cols = ['feature'+str(i) for i in range(x.shape[1])]
normalised_breast = pd.DataFrame(x,columns=feat_cols)
normalised_breast.tail()
تطبيق طريقة العنصر الأساسيّ على البيانات النصيّة
في هذا الجزء سوف نطبق عمليًّا طريقة تحليل العنصر الأساسيّ على مجموعة بيانات سرطان الثديّ، وذلك بعد أن قمنا بعمليّات الجدولة والتطبيع لوضع البيانات في الشكل المناسب لتلائم النموذج عند عمليّات الإدخال. في شفرة البرمجة التالية سوف نقوم بإسقاط projecting المتغيّرات الخاصة بمجموعة بيانات سرطان الثديّ ذات الثلاثين بُعد على مكوّنات رئيسيّة ثنائيّة الأبعاد، ولعمل ذلك سوف نقوم باستيراد صنف PCA من المكتبة اس-كي للتعلّم، ومن ثمّ باستخدام الدّالة n_components نحدّد عدد الأبعاد يساوي 2، وأخيرًا نستخدم الدّالة fit_transform لتجميع البيانات.
from sklearn.decomposition import PCA
pca_breast = PCA(n_components=2)
principalComponents_breast = pca_breast.fit_transform(x)
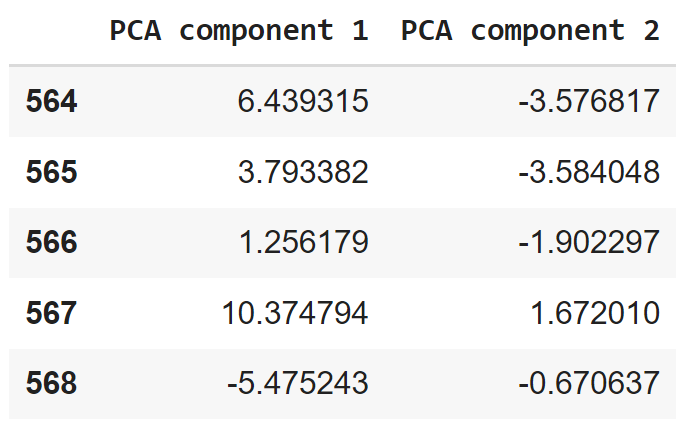
بعد ذلك نقوم بإنشاء DataFrame يحتوي على قيم العناصر الأساسيّة لجميع العيّنات البالغ عددها 569 عيّنة، ومن ثمّ نعرض بعض الأسطر الأخيرة من البيانات لنشاهد قيم العناصر لجميع العيّنات كما في الشكل (3)
principal_breast_Df = pd.DataFrame(data = principalComponents_breast
, columns = ['PCA component 1', 'PCA component 2'])
principal_breast_Df.tail()
بمجرّد حصولك على العناصر الأساسيّة، يمكنك العثور على التّغاير باستخدام الدّالة explained_variance_ratio، ستوفر لنا هذه الدّالة مقدار المعلومات أو التّغاير التي يحتفظ بها كلّ عنصر رئيسيّ بعد إسقاط البيانات على مساحة فرعيّة ذات أبعاد أقلّ، كما في الشفرة البرمجيّة التالية:
print('Explained variation per principal component: {}'.format(pca_breast.explained_variance_ratio_))
output
Explained variation per principal component: [0.44272026 0.18971182]
سوف نلاحظ من المعلومات أعلاه أنّ العنصر الأساسيّ الأوّل يحمل حوالي 44% من المعلومات، بينما العنصر الأساسيّ الثاني يحمل حوالي 19% من المعلومات، وهذا يقودنا إلى أنه عند إسقاط ثلاثين متغيّرًا\خاصيّة من فضاء متعدّد الأبعاد إلى فضاء ثنائيّ الأبعاد، فإننا نفقد حوالي 37% من المعلومات، فعلينا دائمًا عند استخدام طريقة تحليل العناصر الأساسيّة الانتباه إلى حجم و أهميّة المتغيرات، حتى لا نفقد الكثير من المعلومات والتي قد تكون في غاية الأهميّة.
مجموعة بيانات CIFAR – 10
تتكوّن مجموعة بيانات CIFAR-10 (المعهد الكنديّ للأبحاث المتقدّمة) من 60000 صورة ملوّنة بأبعاد (32x32x3) فيها عشرة أصناف، وكلّ تصنيف يحتوي على 6000 صورة. ويتمّ تقسيم البيانات إلى 50000 صورة تتكوّن من مجموعة البيانات التدريبيّة، و10000 صورة تمثل البيانات الاختباريّة. تتمثل الأصناف العشرة في الآتي:
airplane, automobile, bird, cat, deer, dog, frog, horse, ship, truck
استيراد مجموعة بيانات ال CIFAR-10 مقسّمة إلى بيانات اختباريّة وبيانات تدريبيّة، سوف نستخدم الشفرة البرمجيّة التالية:
from keras.datasets import cifar10
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('Training data shape:', x_train.shape)
print('Testing data shape:', x_test.shape)
output
Training data shape: (50000, 32, 32, 3)
Testing data shape: (10000, 32, 32, 3)
الآن سوف نتعرّف على عدد الأصناف الموجودة في مجموعة بيانات المعهد الكنديّ للأبحاث، ومن ثمّ سوف نقوم بعمل قاموس لربط أسماء الأصناف مع الأرقام المقابلة لها.
classes = np.unique(y_train)
nClasses = len(classes)
label_dict = {
0: 'airplane',
1: 'automobile',
2: 'bird',
3: 'cat',
4: 'deer',
5: 'dog',
6: 'frog',
7: 'horse',
8: 'ship',
9: 'truck',
}
print('Total number of outputs : ', nClasses)
print('Output classes : ', classes)
output
Total number of outputs : 10
Output classes : [0 1 2 3 4 5 6 7 8 9]
الآن سوف نجري عمليّة التطبيع على مجموعة البيانات قبل استخدامها في طريقة تحليل العنصر الأساسيّ، ومن ثمّ نتعرّف على شكل البيانات الجديد باستخدام الدّالة reshape كما في الشفرة البرمجيّة التالية:
x_train = x_train/255.0
x_test = x_test/255.0
np.min(x_train),np.max(x_train)
x_train_flat = x_train.reshape(-1,3072)
x_test_flat = x_test.reshape(-1,3072)
في المثال السابق اخترنا أن نمرّر عدد العناصر الأساسيّة مستخدمين المتغيّر n_components، ولكن هنا نريد تمرير مقدار التّغاير الذي نريد أن تلتقطه طريقة تحليل العنصر الأساسيّ، وسوف نستخدم لهذا الغرض 0.9 كمعامل لنموذج تحليل العنصر الأساسيّ، مما يعني أنّ هذه الطريقة سوف تحتفظ بـ 90٪ من التغاير وسيتمّ استخدام عدد العناصر المطلوبة لالتقاط 90٪ من التغاير.كما في الشفرة البرمجيّة التالية:
from sklearn.decomposition import PCA
pca = PCA(0.9)
output
PCA(copy=True, iterated_power='auto', n_components=0.9, random_state=None,
svd_solver='auto', tol=0.0, whiten=False)
سنقوم الآن بالتعرّف على عدد العناصر المستخدمة لالتقاط التّغاير، ومن الناتج أدناه يمكن ملاحظة أنه لتحقيق تباين بنسبة 90٪، تمّ تقليل الأبعاد إلى 99 عنصرًا رئيسيًا بدلًا من الأبعاد الفعليّة والتي عددها كان 3702.
pca.n_components_
output
99
أخيرًا، سنقوم بتطبيق التّحويل transform على كلٍّ من مجموعتي التدريب والاختبار، لإنشاء مجموعة بيانات معدّلة من المتغيرات التي تمّ إنشاؤها باستخدام الدّالة fit.
train_img_pca = pca.transform(x_train_flat)
test_img_pca = pca.transform(x_test_flat)
النّموذج المتسلسل Sequential model
هو أسهل طريقة لبناء نموذج في Keras، إذ أنّه يسمح لنا ببناء النموذج طبقةً بعد طبقة، كلّ طبقة لها أوزانٌ تتوافق مع الطبقة التي تليها.
الكثافة (Dense) هي نوع الطبقة القياسيّ الذي يستخدم في معظم الحالات عند بناء النّموذج المتسلسل، وفي هذا النموذج تتصل كلّ طبقة مع جميع العقد في الطبقة السابقة بالعقد الموجودة في الطبقة الحاليّة.
عدد الدّورات (epochs) هو عدد مرّات تدريب النموذج عبر البيانات، كلما زاد عدد epoch كلما تحسّن النموذج حتى نقطة معيّنة، ومن بعد هذه النقطة سيتوقف النموذج عن التحسّن خلال كلّ مرحلة. بالإضافة إلى ذلك، كلما زاد عدد epoch كلما استغرق تشغيل النموذج وقتًا أطول.
سوف نقوم باستيراد المكتبات التي نحتاج إليها لبناء النموذج
import tensorflow
from tensorflow.keras.optimizers import RMSprop
from keras.models import Sequential
from keras.layers import Dense
From keras.utils import np_utils
ستقوم بتحويل تسميات مجموعتي التدريب والاختبار إلى متجهات ترميزيّة، وسنقوم بتحديد عدد ال epoch وحجم الدّفعة وعدد الأصناف، كما في الشفرة البرمجيّة التالية:
y_train = np_utils.to_categorical(y_train)
y_test = np_utils.to_categorical(y_test)
batch_size = 128
num_classes = 10
epochs = 20
سنقوم الآن بتعريف النموذج التسلسليّ باستخدام الصنف Sequential، وتحديد عدد الطبقات Dense المعينة وإضافتها واحدةً تلو الأخرى باستخدام الدّالة add، وبذلك نحصل على نموذج متسلسل من 5 طبقات
model = Sequential()
model.add(Dense(1024, activation='relu', input_shape=(99,)))
model.add(Dense(1024, activation='relu'))
model.add(Dense(512, activation='relu'))
model.add(Dense(256, activation='relu'))
model.add(Dense(num_classes, activation='softmax'))
model.summary()
output
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 1024) 102400
_________________________________________________________________
dense_1 (Dense) (None, 1024) 1049600
_________________________________________________________________
dense_2 (Dense) (None, 512) 524800
_________________________________________________________________
dense_3 (Dense) (None, 256) 131328
_________________________________________________________________
dense_4 (Dense) (None, 10) 2570
=================================================================
Total params: 1,810,698
Trainable params: 1,810,698
Non-trainable params: 0
________________________________________________________________
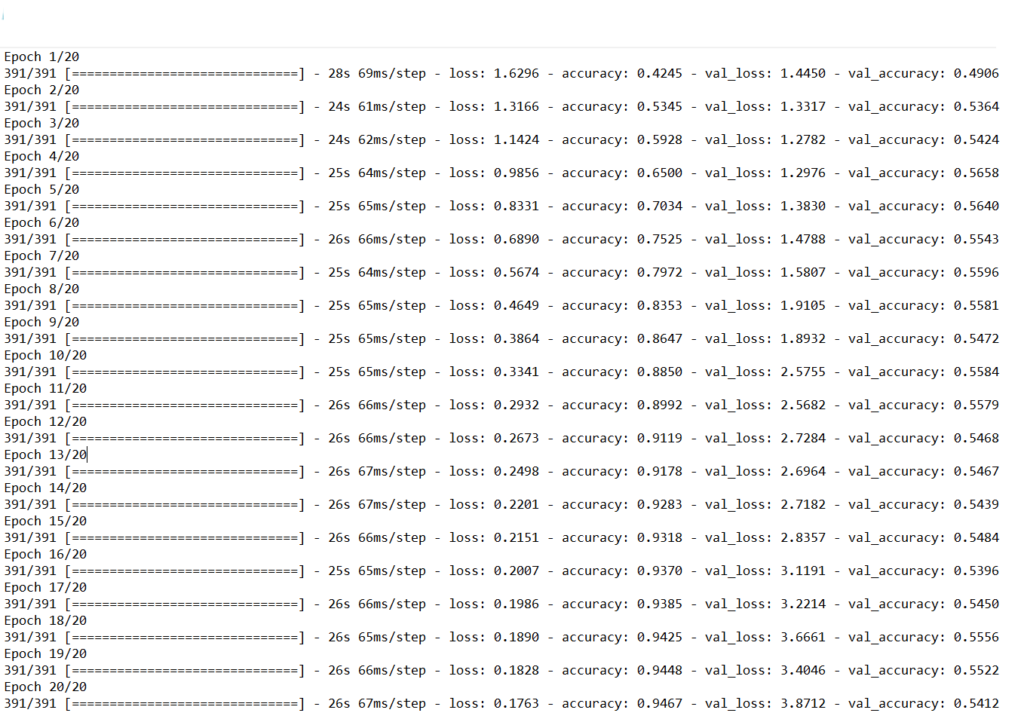
سنقوم الآن بتدريب النّموذج مستخدمين مجموعة البيانات مقسمةً إلى بيانات التدريب وبيانات الاختبار، وذلك لتحسين أداء النموذج فإنّ مكتبة كيراس Keras توفر العديد من المُحسّنات Optimizer التي يمكن التعامل معها مباشرةً.
بغرض تحسين الأداء سنستخدم الصنف (RMSprop(Root Mean Squared Propagation ويوضح الشكل (4) عمليّة التحسّن من خلال توضيح التحسّن في زمن التدريب، وبالإضافة إلى ذلك يمكن ملاحظة أنّ الوقت المستغرَق لتدريب كلّ فترة كان 24 ثانيةً فقط على وحدة المعالجة المركزيّة، ويتضح من ذلك أنّ النّموذج أنجز العمل بصورةٍ جيّدة في بيانات التدريب، حيث حقق دقة 94٪ بينما حقق دقة 55٪ فقط في بيانات الاختبار، وهذا يعني أنّ هنالك مبالغة في تهيئة بيانات التدريب، ومع ذلك فلنتذكر أنه تمّ إسقاط البيانات على 99 بُعدًا من 3072 بُعد، وعلى الرّغم من ذلك فقد قام النموذج بعملٍ رائع.
model.compile(loss='categorical_crossentropy',
optimizer=RMSprop(),
metrics=['accuracy'])
history = model.fit(train_img_pca, y_train,batch_size=batch_size,epochs=epochs,verbose=1,
validation_data=(test_img_pca, y_test))
أخيرًا، دعنا عزيزي القارئ نرى مقدار الوقت الذي يستغرقه النّموذج للتدريب على مجموعة البيانات الأصليّة، ومقدار الدّقة التي يمكن أن يحققها باستخدام نفس نموذج التعلّم العميق.
model = Sequential()
model.add(Dense(1024, activation='relu', input_shape=(3072,)))
model.add(Dense(1024, activation='relu'))
model.add(Dense(512, activation='relu'))
model.add(Dense(256, activation='relu'))
model.add(Dense(num_classes, activation='softmax'))
model.compile(loss='categorical_crossentropy',
optimizer=RMSprop(),
metrics=['accuracy'])
history = model.fit(x_train_flat, y_train,batch_size=batch_size,epochs=epochs,verbose=1,
validation_data=(x_test_flat, y_test))
عند النظر إلى الشكل (5)، نلاحظ أنه من الواضح تمامًا أنّ الوقت المستغرَق للتدريب في كلّ فترة كان حوالي 40 ثانية على وحدة المعالجة المركزيّة، وهو ما يقرب من ضعف الزّمن الذي استغرقه النموذج الذي تمّ تدريبه على استخدام تحليل العناصر الأساسيّة. علاوةً على ذلك، فإنّ دقة التدريب والاختبار أقلّ من الدّقة التي حققتها مع 99 مكوّنًا رئيسيًّا كمدخل للنموذج.
وبذلك ومن خلال تطبيق طريقة تحليل العنصر الأساسيّ على بيانات التدريب، تمكنّا من تدريب خوارزميّة التعلّم العميق الخاصة بنا ليس فقط بسرعة، ولكنها حققت أيضًا دقة أفضل في بيانات الاختبار عند مقارنتها بخوارزميّة التعلّم العميق المدرّبة على بيانات التدريب الأصليّة.
للاطلاع على كامل الشفرة البرمجية يمكنكم زيارة مستوع الجت هب.

الخـــاتمـــمة
عزيزي القارئ أرجو أن تكون قد اتضحت لك الرؤية عند التّعامل مع طريقة تحليل العنصر الأساسيّ، و أن تكون قد تعرّفت على طريقة استخدامها مع نوعين مختلفين من البيانات النصيّة والصوريّة.
إنّ طريقة تحليل العنصر الأساسيّ تعتبر واحدةً من الطرق المستخدمة في تعلّم الآلة والتعلّم العميق، ولكنها ليست الوحيدة فقد تُستخدم مع نوعٍ معيّن من البيانات فتعطي نتيجةً جيّدة وقد يكون العكس، لذلك علينا دائمًا عند التّعامل مع البيانات محاولةُ اختيار الخوارزميّات التي تعطي أفضل النتائج عند تطبيقها، وقد يتطلّب ذلك بعض الوقت والجهد، ولكن نحن كباحثين ومحلّلين للبيانات يجب أن نتابع ونكرّر استخدام الطرق المختلفة للحصول على أفضل النّتائج.
المراجع
- https://builtin.com/data-science/step-step-explanation-principal-component-analysis
- https://ar.wikipedia.org/wiki/
- https://towardsdatascience.com/building-a-deep-learning-model-using-keras-1548ca149d37
- https://www.datacamp.com/community/tutorials/principal-component-analysis-in-python
- https://aiinarabic.com/glossary/