المحتويات
المقدمة
وصلنا عزيزي القارئ الى المقالة الثانية من سلسلة مفهوم خوارزمية آلة المتجه الداعم SVM، حيث تحدثنا في المقالة السابقة مقدمة عن خوارزمية آلة المتّجه الداعم Support Vector Machine عن مبدأ عمل هذه الخوارزمية بشكل عام، وتعرفنا عن أهم المصطلحات المستخدمة فيها، كالهامش بنوعيه المرن وغير المرن ومتجهات الدعم وآلة المتجه الداعم الخطي وغير الخطي .بهذه المقالة سنحاول الدخول بتفاصيل عمل الخوارزمية أكثر، و سنتعلم خطوة بخطوة كيفية استنتاج القيم المثالية لبارمترات معادلة المستوي الفائق في حالة النموذج المرن والصلب. إذا كنت جاهزاً عزيزي القارئ فلنبدأ مقالتنا
ملاحظة: عزيزي القارئ للسهولة في إيصال الفكرة بشكل أوضح ،سنعمل على استنتاج المستوي الفائق المرن والصلب في مجموعة بيانات قابلة للفصل الخطي؛ أي بمعنى سنجد أفضل قيم لمعادلة المستقيم w,b الذي يفصل البيانات بأفضل شكل ممكن .
استنتاج المستوي الفائق الأفضل في حالة النموذج غير المرن Hard Margin

للحصول على أفضل مستوي فائق ،نحتاج إلى إيجاد القيم المثالية لمعادلة الخط الذي يفصل البيانات اي w,b .
حسب الشكل 1، نلاحظ أن جميع النقاط الموجبة هي نقاط موجودة على المتجه الداعم F(x)=1 أو بعده، بالتالي يمكن التعبير عن ذلك بالعلاقة التالية :
wᵀxi̟+b≥1 |i=1……..n1 ( 1)
حيث n1 تُعبر عن عدد العينات الموجبة .
بالتالي لو قُمنا بتعويض أي نقطة من النقاط الموجبة في هذه المتراجحة، سيكون الجواب إما 1 أو أكبر .
نلاحظ أن جميع النقاط السالبة هي موجودة على المتجة الداعم F(x)=-1 أو قبله؛ أي يمكن التعبير عن ذلك بالعلاقة التالية :
wᵀxi_+b≥-1 |i=1……..n2 ( 2)
بالتالي لو قُمنا بتعويض أي نقطة من النقاط السالبة في هذه المتراجحة، سيكون الجواب إما -1 أو أصغر .
نلاحظ أن العلاقتين السابقتين لا تضمن لنا الحصول على أفضل مستو\ي فائق , لنقم بأخذ مثال يوضح ذلك
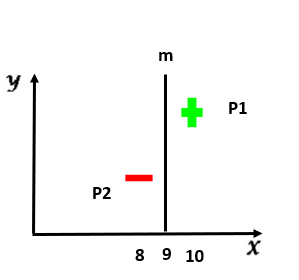
بالملاحظة نجد أن معادلة المستقيم m تُحقق العلاقتين 1 و 2 محققة من أجل النقاط (8,0 ) ,
(10,0) و سنوضح ذلك :
لدينا من معادلة المستقيم
X=9 ⇒ X – 9 =0 (1- 2)
بتعويض النقطة الموجبة p 1 في المعادلة (1- 2) نجد :
10 -9 =1 ⇒ 1 ≥ 1
بالتالي العلاقة 1 محققة .
بتعويض النقطة السالبة p 2 في المعادلة (1- 2) نجد :
8-9= -1 ⇒ -1 ≥ -1
بالتالي العلاقة 2 محققة
ولكن إذا قُمنا بعملية تحليل بسيطة، نلاحظ أن المستوي الفائق m ليس مثالياً ؛ لأن من صفاته أن يكون الهامش مابينه وبين النقاط الواقعة على المتجهات الداعمة أكبر ما يمكن ،وبالملاحظة هنا يمكننا إيجاد مستوي فائق أفضل ويحقق المطلوب كالتالي :
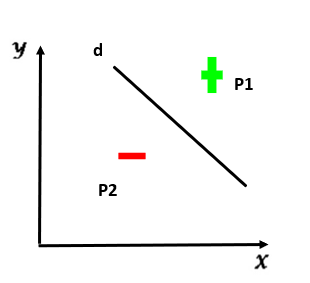
نستنتج كلما كان الهامش أكبر مع تحقق العلاقتين 1 و 2 كلما حصلنا على أفضل مستوي فائق بالتالي أصبح هدفنا هو إيجاد أقصى قيمة للهامش µ مع مشروطية تحقق العلاقتين 1و 2 .
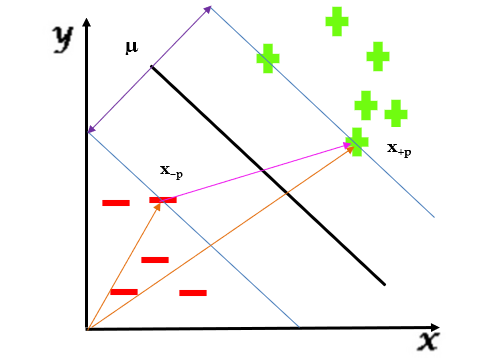
يجب أولاً الحصول على قيمة µ ،ومن بعدها نعمل على ايجاد القيمة القصوى لها ، ويتم ذلك من خلال أخذ شعاعين وليكن x-p و x+p وحساب ناتج طرحهما ولكن نلاحظ أن ناتج طرح الشعاعين
( x+p – x-p) لايعبر عن المسافة µ لأنهما غير متوازيين بالتالي يجب أن نفكر بطريقة رياضية لجعل ناتج طرح الشعاعين موازٍ لقيمة µ أي في اتجاه µ . كما في الشكل 4
ملاحظة : عزيزي القارئ عندما نريد تغيير اتجاه شعاع وليكن a بإتجاه شعاع ثاني وليكن b ، عندها نقوم بعملية ضرب نقطي dot product ما بين الشعاع a وشعاع واحدي unit vector بإتجاه الشعاع b .
بالتالي ماعلينا فعله هو ضرب الشعاع الناتج (x+p – x-p ) كما في الشكل 4 بمتجه واحدي unit vector في نفس اتجاه الهامش µ .
حسب الشكل 5،نلاحظ أن الشعاع w عمودي على المستوى الفائق ، بالتالي هو مواز للهامش µ أي في نفس اتجاهه وللتأكد من ذلك سنقوم بعملية برهان لذلك :
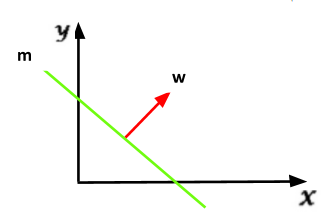
بفرض أن معادلة المستقيم m هي wᵀx+b=0
وبفرض أن الشعاعw هو عمودي على هذا المستقيم
إذا اعتبرنا أن قيمةb=0 أي أن المستقيم سيمر من مبدأ الإحداثيات كما يلي :
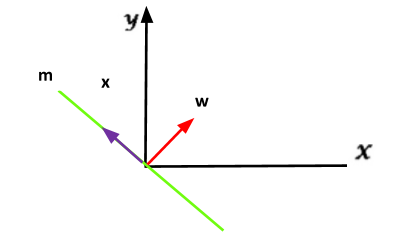
وتصبح معادلة المستقيم wᵀx=0
اذا قُمنا سوياً بعملية تحليل بسيطة للمعادلة wᵀx نلاحظ أنx تعبر عن أي شعاع موازٍ ومطابق للمستقيم m ولدينا من الفرض wᵀx=0بالتالي w. x =0 ونحن نعلم إذ كان الضرب النقطي بين شعاعين هو صفر، بالتالي هذان الشعاعان هما متعامدان .
بالتالي نستنتج أن الفرض كان صحيحاً ومنه الشعاع w هو عمودي على المستوى الفائق أي يوازي الهامش µ .
تبقى علينا تحويل الشعاع w الى شعاع واحدي .
ملاحظة : عزيزي القارئ يتم تحويل الشعاع a إلى شعاع واحدي Unit Vector من خلال قسمته على النظيم magnitude .
بالتالي تصبح قيمة الهامش µ :
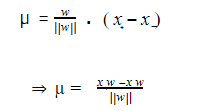
بالمطابقة مع العلاقتين 1 و 2 نجد :
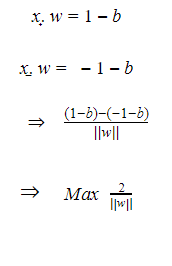


y̟=1
من العلاقة 2 نستنتج أن الخرج الموافق لأي نقطة سالبة هو -1، بالتالي يمكن أن نعبر عن ذلك من خلال المعادلة التالية :
y̠= -1
بالتالي إذا ضربنا y+ في العلاقة 1 نجد :
y+(WT x+ + b) ≥ 1 ( 3 )
وإذا ضربنا -y– في العلاقة 2 نجد :
y–( WT xi– + b) ≥ 1 ( 4 )
نستنتج من العلاقتين 3 و 4 العلاقة العامة :
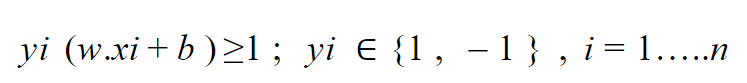
n تعبر عن عدد العينات الكلية .
ملاحظة :
wᵀ xi =w .xi
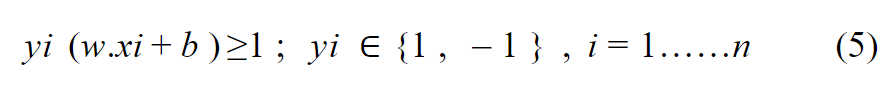
بالتالي أصبح الهدف النهائي:
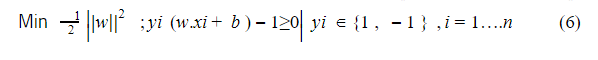
نلاحظ أن هذه المشكلة تعبر عن constrained optimization problem أي مشكلة أمثلية مقيدة ، ويعتبر حل هكذا نوع من المسائل صعب للغاية ، بالتالي عملية إيجاد القيمة المثالية لـ w,b التي تعطي أفضل مستوي فائق تُعتبر صعبة للغاية ولكن إذا تم تحويل هذه المشكلة إلى
unconstrained optimization problem أي مشكلة أمثلية غير مقيدة بالتالي تصبح عملية إيجاد القيمة المثالية ل w,b سهلاً للغاية .
كيف يمكن التحويل من مشكلة أمثلية مقيدة إلى مشكلة أمثلية غير مقيدة ؟
بإستخدام طريقة لاغرانج .
خطوات خوارزمية Lagrange
من أجل كل قيد يتم تشكيل معادلة لاغرانج، والتي تعطى بالعلاقة التالية :
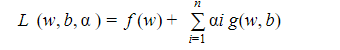
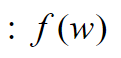
التابع المطلوب إيجاد القيمة الصغرى له .
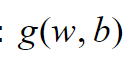
القيد المطبق على التابع .
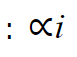
معامل لاغرانج بحيث من أجل كل قيد يتم استخدام معامل خاص به .
gw,b≤0 ;
بالمطابقة مع العلاقة العامة لمعادلة لاغرانج نجد :
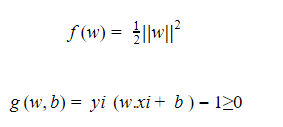
بالملاحظة أن الشرط gw,b≥0 بالتالي يجب عكس اشارته من خلال الضرب ب -1
بالملاحظة لدينا شرط واحد، بالتالي نحتاج الى معامل لاغرانج وحيد وليكن α
بالتالي تُصبح معادلة لاغرانج
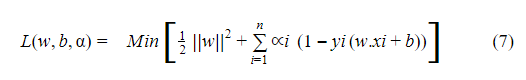
يتم إيجاد القيم الصغرى من خلال اشتقاق المعادلة Ld w,b,α بالنسبة ل w,b,α ومساواتها بالصفر.
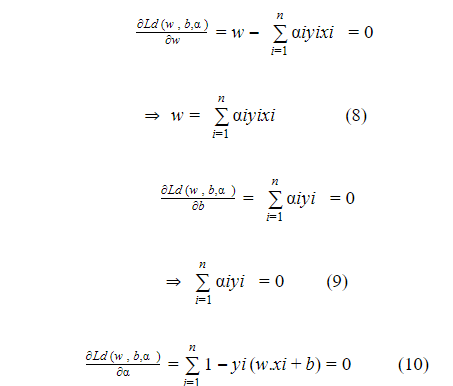
نلاحظ من المعادلات السابقة يمكننا إيجاد قيمة w التي تعتمد على قيمة b و ،بالتالي يجب علينا إيجاد القيمة المثالية ل b و α وبالملاحظة أن المعادلة 7 تعبر عن مسألة مثالية ولكن لاتساعدنا في ايجاد القيم المثالية، بالتالي يجب علينا تحويل المعادلة 7 الى مسألة مثالية تساعدنا في إيجاد القيم المثالية وذلك باستخدام طريقة dual البسيطة .
خطوات خوارزمية dual
- تشكيل الصيغة العامة للمعادلة dual
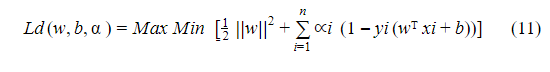
- حل المعادلة التالية :
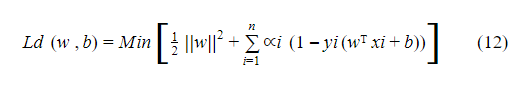
يتم إيجاد القيم الصغرى من خلال اشتقاق المعادلة Ld w ,b بالنسبة ل w,b ومساواتها بالصفر ، ونلاحظ سابقاً أننا قُمنا باشتقاق هذه المعادلة بالنسبة ل w ,b , بالتالي تبقى علينا فقط التعويض :
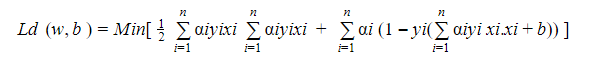
- كتابة المعادلة السابقة بأفضل شكل ممكن .
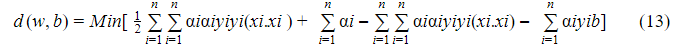
ولكن:
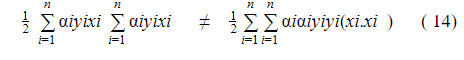
ولكن نتيجة هذين المقدارين غير المتساويين و لإثبات ذلك نأخذ المثال التالي :
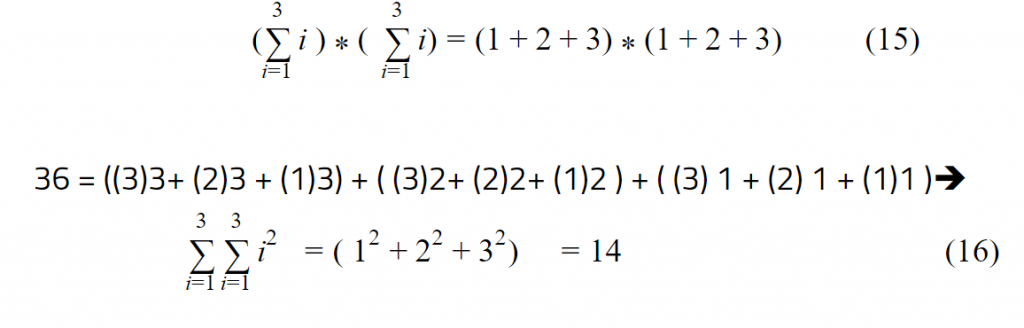
بالتالي يجب التفكير في حيلة رياضية لجعل المقدارين في المعادلة 14 متساويين ويتحقق ذلك من خلال استخدام متحول ثانٍ وليكن j كالتالي :
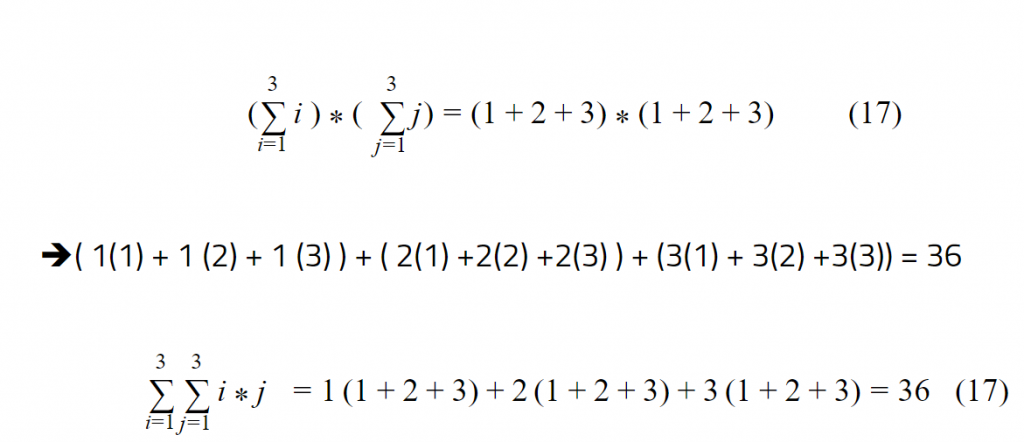
نلاحظ بعد استخدام متحول آخر يمكننا القول أن:
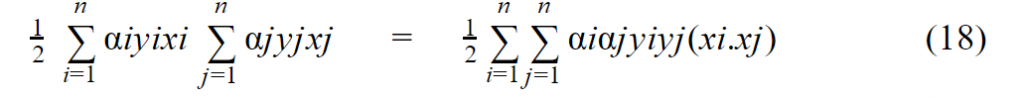
بالتالي تصبح المعادلة 13 بالشكل التالي :
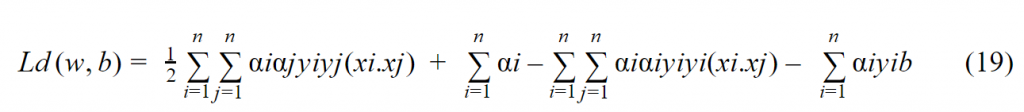
لدينا سابقاً من المعادلة 9 :
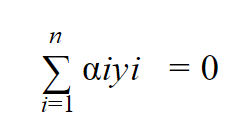
بالتالي تصبح المعادلة بعد تبسيطها بأفضل شكل ممكن :
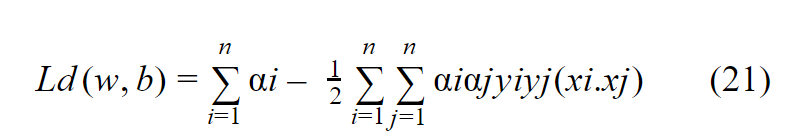
نعوض المعادلة 21 في المعادلة 11 فنجد :
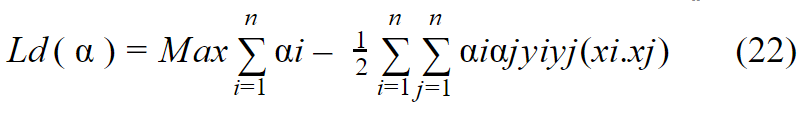
من المعادلة السابقة نحتاج الى:
- إيجاد القيمة القصوى للمعادلة 22 من خلال إيجاد القيمة المثالية ل ، ولكن تُعتبر هذه المشكلة بسيطة جداً فيوجد عدة مكاتب في البايثون تدعم حل هذا النوع من المشاكل أو عن طريق خوارزمية gradient descent يمكن إيجاد القيمة المثالية ل .
- ايجاد القيم المثالية ل w,b .
من المعادلة 8 نستنتج :
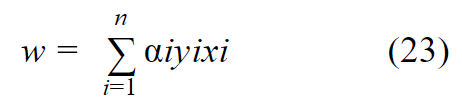
من المعادلة 5 نجد:
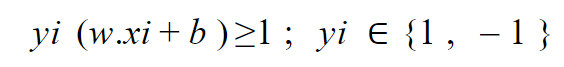
نحن نعلم أن الخط الفاصل بين البيانات يكون في منتصف المسافة ما بين المتجهات الداعمة بالتالي :
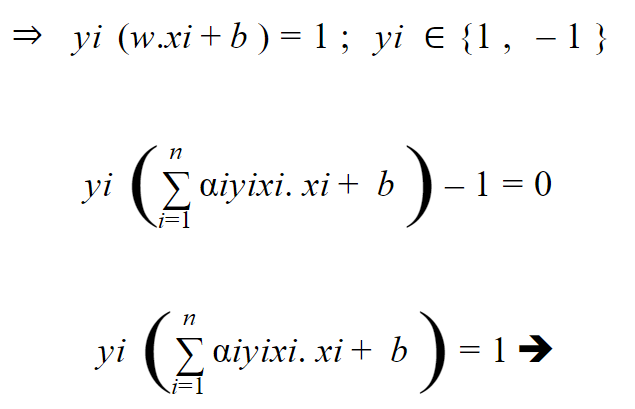
نضرب طرفي المعادلة ب yi فنجد :
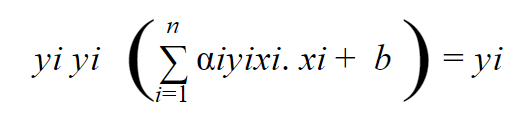
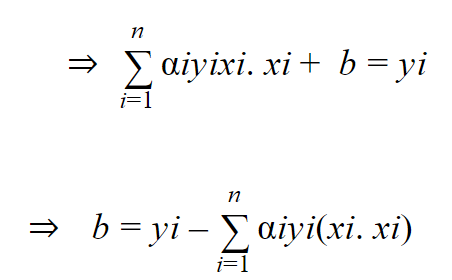
ولكن هنا اعتبرنا أن لدينا نقطتين سالبة وموجبة، أما من أجل معرفة قيمة b من أجل جميع نقاط البيانات الواقعة على المتجهات الداعمة نوجد المتوسط الحسابي بالتالي :
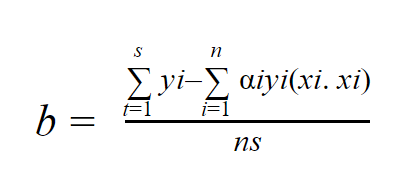
حيث ns هي عدد النقاط الواقعة على المتجهات الداعمة .وبذلك نكون قد وصلنا لمعادلة المستوي غير المرن وهوامشه.
استنتاج المستوي الفائق الأفضل في حالة النموذج المرن Soft Margin
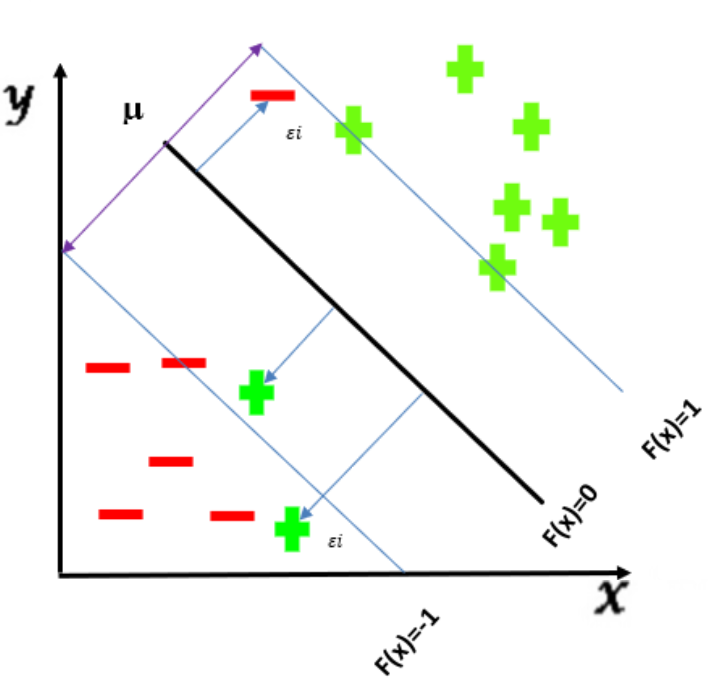
في هذا النموذج يتم السماح لبعض النقاط القليلة التي تؤثر على عملية الفصل خطياً أن يتم تصنيفها بشكل خاطئ سواء كانت ضمن منطقة الهامش أو خارجه، بالتالي يتم إضافة معامل يعبر عن نسبة الخطأ في كل نقطة من نقاط التدريب سواء كانت مُصنفة بشكل صحيح أم خاطئ .
بالتالي يُمكن التعبير عن النقاط الموجبة بالعلاقة التالية :
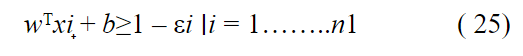
حيث n1 تُعبر عن عدد العينات الموجبة .
قيمة i هي صفر بالنسبة للنقاط التي تنتمي للصنف الموجب، وتم تصنيفها من قبل الخوارزمية على أنها تابعة للصنف الموجب، وقيمتها أكبر من الصفر بالنسبة للنقاط التي تنتمي للصنف السالب ،وتم تصنيفها من قبل الخوارزمية على أنها تابعة للصنف الموجب .
بالتالي يُمكن التعبير عن النقاط السالبة بالعلاقة التالية :
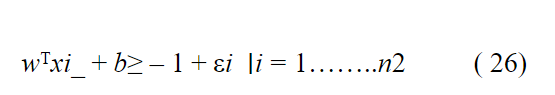
حيث n2 تُعبر عن عدد العينات السالبة .
قيمة i هي صفر بالنسبة للنقاط التي تنتمي للصنف السالب وتم تصنيفها من قبل الخوارزمية على أنها تابعة للصنف السالب، وقيمتها أكبر من صفر بالنسبة للنقاط التي تنتمي للصنف الموجب وتم تصنيفها من قبل الخوارزمية على أنها تابعة للصنف السالب .
من العلاقتين 25 و 26 نستنتج :
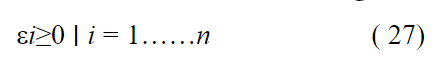
حيث n تُعبر عن عدد العينات الكلي ( الموجبة – السالبة ) .
كما تحدثنا في الأعلى في النموذج غير المرن أن العلاقتين 25 و 26 غير كافيتين للحصول على أفضل مستوي فائق ،بالتالي سنعمل على إيجاد أكبر قيمة لعرض الطريق أي الهامش مع مشروطية المحافظة على شرط تحقق العلاقتين 25 و 26 .
بنفس الطريقة السابقة المتبعة في النموذج غير المرن ،يجب اولاً إيجاد معادلة الهامش ثم نوجد القيمة الكبرى لهذه المعادلة فنحصل على :
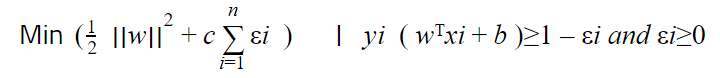
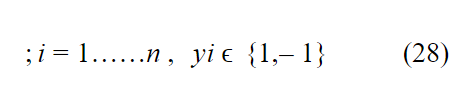
بالملاحظة تم الأخذ بعين الاعتبار مجموع الأخطاء مضروب بالمعامل c ويسمى معامل Regularization أي معامل التنعيم والغاية منه :
في الطرف الأول كُنا نسعى لإيجاد أصغر قيمة للمقدار
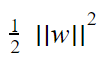
أي بمعنى آخر إيجاد أكبر قيمة لعرض الهامش، ولكن نلاحظ كلما كان عرض منطقة الهامش أكبر ،كلما كان عدد النقاط الواقعة ضمن هذه المنطقة أكبر ، وهذا ما يتناقض مع مبدأ عمل المستوي الفائق المرن، بحيث يجب أن تكون عدد النقاط الواقعة ضمن هذه المنطقة إما معدومة أو قليلة جداً ،لذلك يتم إضافة المعامل c لتجنب الإفراط الكبير في عرض الهامش .
نلاحظ أن هذه المشكلة تعبر عن constrained optimization problem أي مشكلة أمثلية مقيدة ،ويعتبر حل هكذا نوع من المسائل صعب للغاية بالتالي عملية ايجاد القيمة المثالية لـ w,b التي تعطي أفضل مستوي فائق تُعتبر صعبة للغاية ولكن إذا تم تحويل هذه المشكلة إلى
unconstrained optimization problem أي مشكلة أمثلية غير مقيدة ، بالتالي تصبح عملية إيجاد القيمة المثالية ل w,b سهلاً للغاية .
كما في فقرة استنتاج الهامش غير المرن سنقوم بتطبيق خوارزمية لاغرانج فنجد :
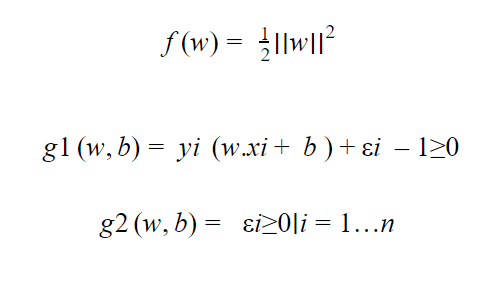
نلاحظ أن الشرطان (g1(w,b و( g2(w,b ليسا أصغر من الصفر، لذلك سيتم عكس إشارة المتراجحة من خلال الضرب ب -1
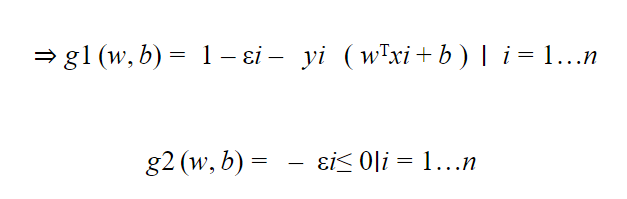
يتم إيجاد القيم الصغرى من خلال اشتقاق المعادلة (Ld (w,b,ε,α,β بالنسبة لـ w,b,ε,α,β ومساواتها بالصفر .
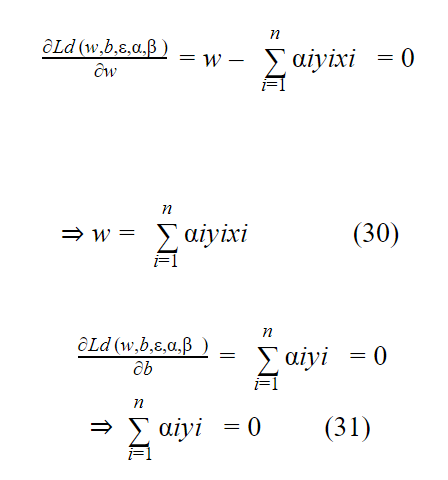
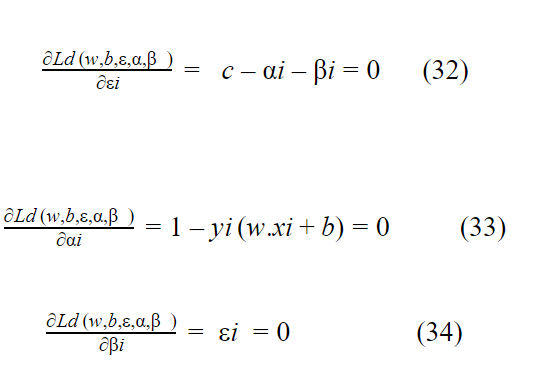
وبالملاحظة أن المعادلة 29 تعبر عن مسألة مثالية ،ولكن لاتساعدنا في إيجاد القيم المثالية بالتالي يجب علينا تحويل المعادلة 7 الى مسألة مثالية تساعدنا في إيجاد القيم المثالية وذلك باستخدام طريقة dual البسيطة .
خطوات خوارزمية dual
- تشكيل الصيغة العامة للمعادلة dual
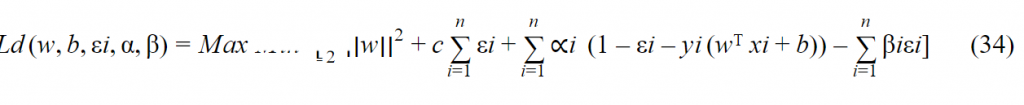
حل المعادلة التالية :
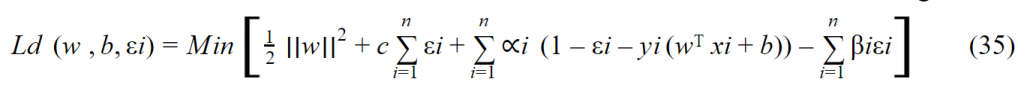
يتم إيجاد القيم الصغرى من خلال اشتقاق المعادلة ( Ld (w ,b,εi بالنسبة لـ w, b, Σi ومساواتها بالصفر , ونلاحظ سابقاً أننا قُمنا باشتقاق هذه المعادلة بالنسبة لـ , Σi,w ,b بالتالي تبقى علينا فقط التعويض :
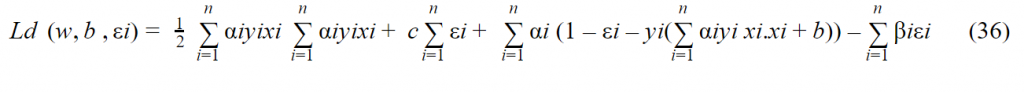
نكتب المعادلة 37 بأفضل شكل ممكن .
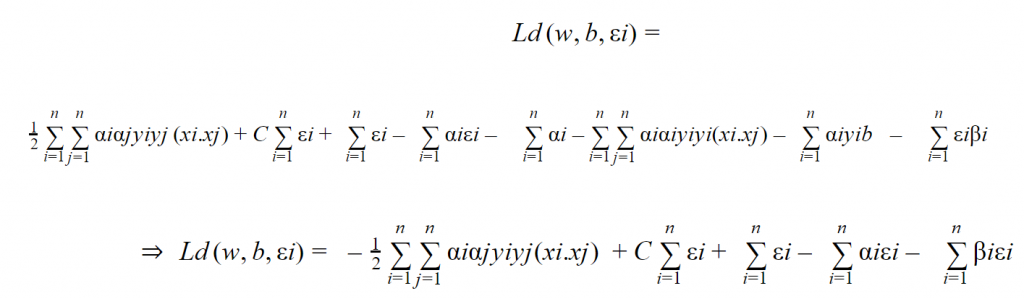
من 32 نستنتج :

بالتعويض في المعادلة 35 نجد :
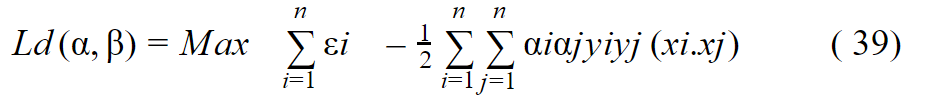
ولكن هنا قد تخلصنا من β واصبحت المعادلة مشروطة فقط بقيمة α ،بالتالي تصبح القيود الجديدة كالتالي:
القيد الأول :
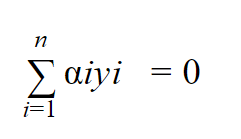
القيد الثاني :
نحن نعلم أن αi≥0 و βi≥0 بالتالي نستنتج من المعادلة 32 أن :
αi=c- βi
بالتالي يمكن كتابة العلاقة السابقة، كما يلي c- βi≥0 ومنه نستنتج أن c≥βi ومنه
0≤α≤c
بالتالي :
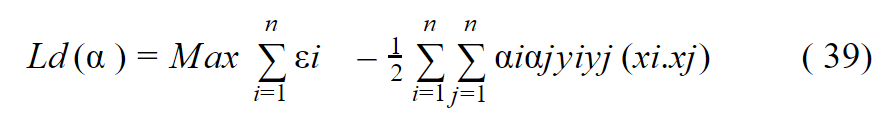
وعليه:
- يمكن إيجاد القيمة القصوى للمعادلة 39 من خلال إيجاد القيمة المثالية لـ α ولكن تُعتبر هذه المشكلة هي بسيطة جداً، فيوجد عدة مكاتب في البايثون تدعم حل هذا النوع من المشاكل أو عن طريق خوارزمية gradient descent و يمكن إيجاد القيمة المثالية لـα.
- ولإيجاد القيم المثالية لـ w,b
من المعادلة 30 نستنتج قيمة w :
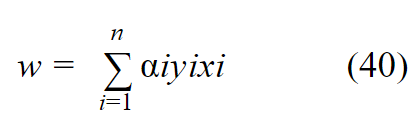
من المعادلة 28 نستنتج قيمة b :
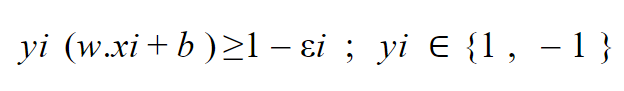
وحيث أن الخط الفاصل بين البيانات يكون في منتصف المسافة ما بين المتجهات الداعمة بالتالي :
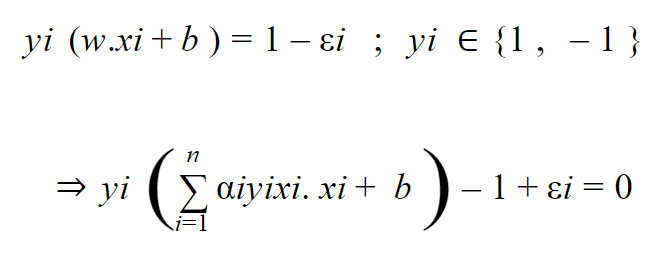
من المعادلة 34 لدينا
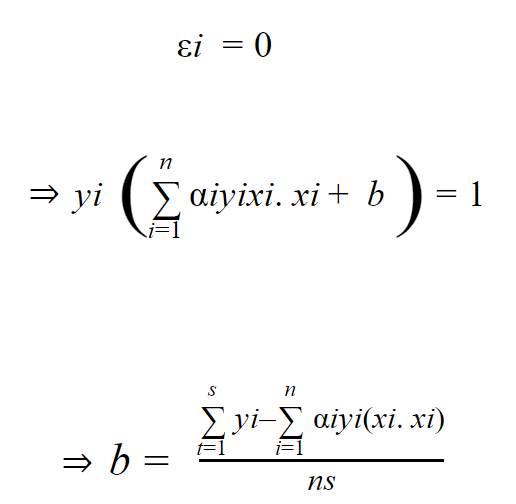
حيث ns هي عدد النقاط الواقعة على المتجهات الداعمة ، وبذلك نكون قد وصلنا إلى استنتاج معادلة المستوي الفائق المرن.
الخاتمة
وبهذا نكون قد انتهينا من السلسلة الخاصة بخوارزمية آلة المتجه الداعم ،والتي تُعتبر من
أهم الخوارزميات المستخدمة في التعلم اآلي والتي كانت تبحث على أفضل طريقة لتقسيم البيانات إلى مجموعتين بوضع مستوي فائق hyperplane بينهما بغض النظر عن طبيعة البيانات سواء كانت قابلة للفصل الخطي أو لا، بحيث تعلمنا في المقال الأول من هذه السلسلة مقدمة عن خوارزمية آلة المتّجه الداعم Support Vector Machine مبدأ عمل هذه الخوارزمية بشكل ٍ عام وتعرفنا على كافة المفاهيم المستخدمة فيها أما في هذا المقال توسعنا أكثر فأكثر في هذه الخوارزمية من خلال التعمق فيها رياضياً ، من خلال استنتاج معادلة المستوي الفائق بنوعيه المرن وغير المرن خطوة بخطوة بالاعتماد على طريقة لاغرانج التي استخدمناها في تحويل المشكلة التي لدينا من مشكلة أمثلية مقيدة إلى مشكلة أمثلية غير مقيدة ،وهذا ما يبسط ويسهل عملية استنتاج بارامترات معادلة المستوي الفائق أي b, w بأفضل شكل ممكن .
المراجــــع
[1]understanding-mathematics-behind-support-vector-machines/