خوارزمية اكتشاف القيم المتطرفة المحلية Local Outlier Factor

المقدّمة 

تشير التحويلات غير الطبيعيّة في بطاقات الائتمان إلى عملية احتيال وسرقة وأنه ينبغي على النظام المسؤول كشف مثل هذه التحويلات ومنع إجرائها [1]. الأمر مشابه في أنظمة الحماية حيث يشير السلوك غير الطبيعيّ إلى عمليّة اختراق وإنه ينبغي أيضاً على النظام كشف عملية الاختراق والتصدي لها، لنطرح مثالاً بسيطاً لتوضيح الصورة أكثر على سبيل المثال عند نسيان المستخدم لـكلمة المرور الخاصة به فمن الطبيعي أن يقوم هذا المستخدم بإجراء خمس محاولة على الأقل لتسجيل الدخول لعله يتذكر كلمة المرور وهذا أمر طبيعي يحدث معاً جميعاً ولكن في حال تجاوزت هذه المحاولات الخمس مرات وزادت بشكل كبير فمن الأرجح أنه تمثل عملية اختراق [2]. حيث عملت تقنيات الكشف عن الحالات الشاذة Anomaly Detection على دراسة وكشف السلوك غير الطبيعي الذي يثير الشكوك ويمثل عمليات اختراق او ماشبه ذلك وتعد هذه التقنية من التقنيّات الشائعة التي لاقت اهتماماً بالغًا لدى العديد من الباحثين والشركات الكبرى في مجالات عديدة ومتنوعة.

في هذا المقال سوف نتحدّث عن أحد الخوارزميّات المستخدمة في تحديد القيم الشاذّة وهي خوارزميّة اكتشاف القيم المتطرفة المحلية Local Outlier Factor. لكن ماذا نقصد بـالقيمة المتطرفة المحلية Local Outlier؟

توجد أساليب عديدة ومتنوعة لتحديد القيم المتطرفة ولكن عندما يتم الاعتماد على الجوار المحليّ لـتحديد هذه القيم فعندها تكون هذه القيم هي متطرفة محلية وهذا جوهر عمل خوارزميّة الكشف عن القيم المتطرفة المحلية LOF حيث تقرر في ما إذا كانت النقطة متطرفة أم لا بناءً على كثافة النقاط المجاورة لها. لفهم هذه الخوارزميّة بشكل جيد لابد من المرور على بعض المفاهيم الأساسيّة وهي:

• مفهوم المسافة k-distance  و  عدد الجيران k-neighbors.
• مفهوم مسافة قابلية الوصول (Reachability distance (RD.
• مفهوم كثافة قابلية الوصول المحلية (Local reachability density (LRD.
• مفهوم عامل القيم المتطرفة المحلية (Local Outlier Factor (LOF.

مفهوم المسافة وعدد الجيران

أوّلاً المسافة: تمثل المسافة بين نقطة البيانات ولتكن xᵢ مع أبعد نقطة من جيران النقطة xᵢ المثال التالي يوضح هذا التعريف بشكل جيد.

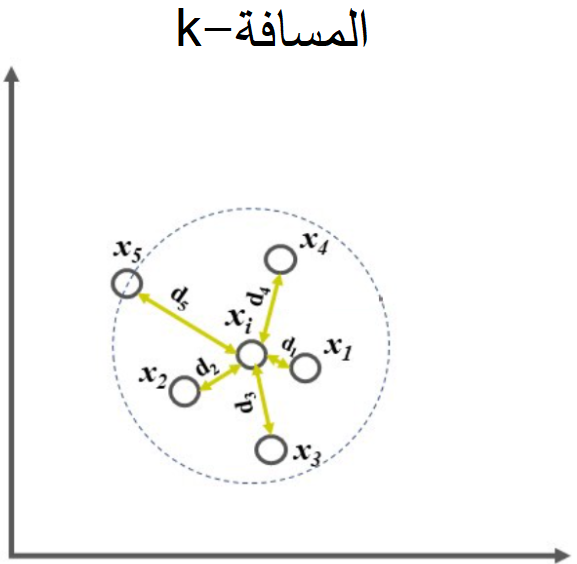
كما نلاحظ من الشكل 1 لدينا k=5 (القيمة k هي قيمة اختيارية) وبالتالي علينا اختيار أقرب 5 نقاط من نقطة البيانات x_i، حيث تمثل القيمة distance(x_i)-5 المسافة بين نقطة البيانات x_i وخامس أبعد نقطة من الجيران (أي النقطة x₅) يرمز لهذه المسافة بالرمز d₅.

القيمة 4-distance(x_i) تمثل المسافة بين نقطة البيانات x_i ورابع أبعد نقطة من الجيران (أي النقطة x₄) يرمز لهذه المسافة بالرمز d₄، نفس الأمر بالنسبة لباقي النقاط.

نلاحظ أن النقطة x₅ هي أبعد جار عن النقطة x_i وبالتالي تكون قيمة الـ   k-distance(x_i) تساوي d₅.

ثانياً عدد الجيران:  تدعى أيضاً الجيران الأقرب Nearest Neighbors وهي مجموعة تحتوي على أقرب النقاط (الجيران) لنقطة البيانات xᵢ يرمز لها بالرّمز N_k(xᵢ). الشكل التالي (2) يوضح التّعريف بشكلٍ جيد.

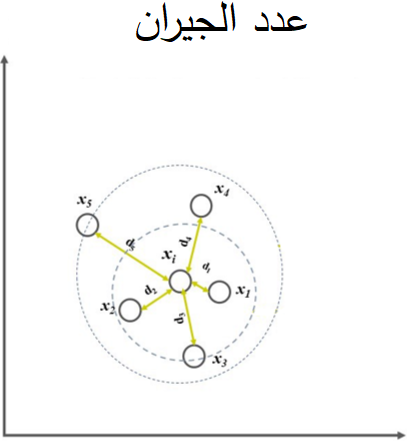
كما نلاحظ من الشكل 2 وبفرض نريد تحديد أقرب 5 نقاط من نقطة البيانات x_i، في البداية نعبر عن المجموعة التي تحتوي أقرب 5 نقاط من نقطة البيانات بالشكل N_k=5(x_i) وتكون المجموعة وبحسب الشكل 2 تحتوي على النقاط {x₅,x₄,x₃,x₂,x₁}

| (N_k(xᵢ | تشير إلى العدد الإجماليّ لنقاط البيانات الموجودة في جوار النقطة xᵢ (النقاط الأقرب) بالنسبة لقيمة k المُعطاة.

لكن السؤال الذي يطرح نفسه هل من الممكن أن يكون | (N_k(xᵢ | أكبر أو يساوي قيمة k، وكيف يمكن أن يكون هذا؟

لنأخذ مثالاً، بفرض أنّ لدينا أربع نقاط A و B و C و D (كما هو موضح في الصّورة أدناه).

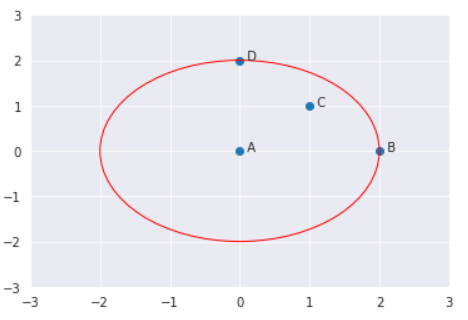
إذا كانت K=2 بالتالي | (N₂(A | للنقطة A سوف تكون النقاط B,C,D. نظراً لأنّ النقطتان  D , C يبعُدان بنفس المسافة عن A. هنا قيمة الـ  K تساوي 2 لكنّ عدد النقاط في جوار النقطة A أي ||N₂(A)|| يساوي 3. لذلك ||N_k(point)|| قد يكون أكبر أو يساوي K. 

مفهوم مسافة قابلية الوصول المحلية (RD)

دعنا نعرّفها في البداية على أنّها المسافة بين نقطتين ولتكن النقطتان على سبيل المثال A و B ، لكن يتمّ تعريفها رياضيّاً على أنّها المسافة الأكبر بين مسافتين: المسافة الأولى هي المسافة بين النقطتين A و B والمسافة الثانية هي المسافة-k للنقطة الثانية B. المعادلة التالية توضح التعريف بشكل جيّد.

reachability-distance _k(A,B)=max{k-distance(B),d(A,B)}

وبالتالي نفهم من ذلك أنّ مسافة قابلية الوصول  بين نقطتين إما يساوي المسافة المباشرة بين النقطتين أو المسافة-k للنقطة الثانية، حيث النقطة B هي النقطة في المركز و النقطة A هي نقطة قريبة منها.

 إنّ مقياس المسافة هو مقياس محدّد مقياس اقليدي، ماهلانوبس(Euclidean  ، Mahlanobce ، وما يشابه ذلك).

الصورة التالية تمثل مسافة الوصول لنقطةٍ ما إلى جيران مختلفين:

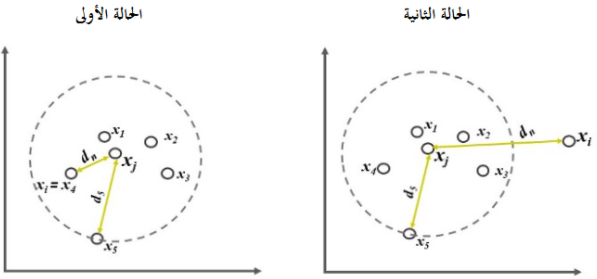
كما هو موضح في الشكل 4، فإنه بالنسبة للحالة الأولى النقاط موجودة داخل الدّائرة أي بُعد هذه النقاط عن النقطة x_j أصغر من (x_j)k-distance مسافة k، بالتالي تكون مسافة قابلية الوصول RD لنقطة المركز x_j  هي (x_j)k-distance، أمّا بالنسبة للحالة الثانية النقطة  x_i بُعدها عن نقطة المركز x_j أكبر من (x_j)k-distance، بالتالي تكون مسافة قابلية الوصول RD بين النقطتين x_j  و x_i  هي المسافة المباشرة بين النقطتين.

مفهوم كثافة قابلية الوصول المحلية (LRD)

هو معكوس لمتوسّط ​​مسافة قابليّة الوصول RD بين نقطة ما وجيرانها، يتمّ حساب مسافات قابلية الوصول RD لجميع الجيران الأقرب للنقطة بتحديد كثافة قابليّة الوصول المحليّة (LRD) لتلك النقطة. وتعدّ كثافة قابليّة الوصول المحليّة LRD مقياسًا لتحديد كثافة k لتكون قريبة من نقطة معيّنة.

يتمّ تعريف كثافة قابليّة الوصول المحليّة بالمعادلة الرياضيّة التالية:

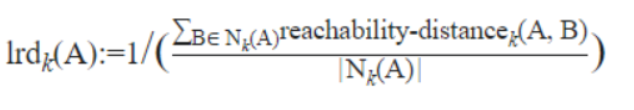
تخبرنا قيم كثافة الوصول المحلية LRD إلى مدى بُعد النقطة المدروسة عن أقرب مجموعة من النقاط. حيث تشير القيم المنخفضة لـكثافة الوصول المحلية LRD إلى أنّ أقرب مجموعة هي بعيدة عن النقطة المدروسة والعكس صحيح. وهذا تفسير للعلاقة الرياضيّة السابقة (علاقة كثافة الوصول المحلية LRD) حيث كلما زاد متوسّط ​​مسافة الوصول RD (أي يبعد الجيران عن النقطة)، كلما كانت الكثافة أقلّ حيث العلاقة هنا عكسية. 

مفهوم عامل القيم المتطرفة المحلية (LOF)

يتمّ استخدام كثافة قابليّة الوصول المحليّة في حساب عامل القيم المتطرفة المحلية LOF  حيث يتمّ تعريفه بالعلاقة الرياضيّة التالية

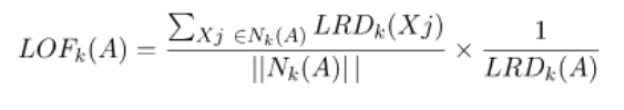
يتمّ استخدام كثافة قابليّة الوصول المحليّة LRD لكلّ نقطة للمقارنة بمتوسّط كثافة قابليّة الوصول المحليّة ​​LRD لجيرانها K. حيث أن عامل القيم المتطرفة المحلية LOF هي نسبة متوسّط كثافة قابليّة الوصول ​​LRD لجيران K لـ A إلى كثافة قابليّة الوصول المحلية LRD لـ A.

وفقاً للمعادلة أعلاه، إذا لم تكن النقطة خارجيّة  (أي تكون inlier)، فإنّ نسبة متوسّط كثافة قابليّة الوصول المحليّة ​​LRD للجيران تساوي تقريبًا كثافة قابليّة الوصول المحليّة LRD للنقطة (لأنّ كثافة النقطة وجيرانها متساوية تقريبًا، بالتالي كثافة قابليّة الوصول للنقطة سوف يتساوى مع متوسّط كثافة قابليّة الوصول لنقاط الجوار). في هذه الحالة تكون القيم المتطرفة المحلية LOF تساوي تقريبًا 1.

 من ناحية أخرى ، إذا كانت النقطة متطرفة فإنّ كثافة قابلية الوصول المحلية LRD لنقطةٍ ما يكون أقلّ من متوسّط كثافة الوصول المحلية ​​LRD للجيران. بالتالي ستكون القيم المتطرفة المحلية LOF عالية.

مثال توضيحيّ: 

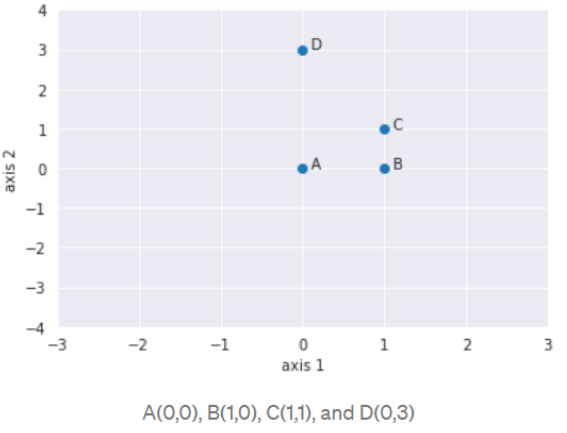
بفرض لدينا أربع نقاط في المستوى الإحداثيّ هما: 

A(0,0), B(1,0), C(1,1) , D(0,3) 

سوف نستخدم خوارزميّة معامل القيم المتطرفة LOF لاكتشاف حالة متطرفة  واحدة من بين هذه النقاط الأربع.

بفرض كان لدينا K=2.

باتباع الإجراءات التي  تمت مناقشتها أعلاه:

أوّلاً: نقوم بحساب المسافة-k و المسافة بين كلّ زوجين من النقاط، بعد ذلك سوف نقوم بإيجاد أقرب جارين من أجل كلّ النقاط وذلك لأننا افترضنا  أنّ K=2. 

تنويه: سوف يتمّ استخدام مسافة مانهاتن Manhattan distance كمقياسٍ للمسافة حيث يبين الجدول 1 المسافة بين كل زوجين من النقاط.

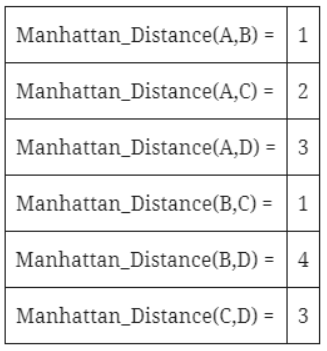
يمثل الجدول السابق المسافة بين كلّ زوجين من النقاط وفقاً لمقياس مانهاتن. الآن سوف نقوم بحساب المسافة-k من أجل النقاط الأربع.

• حساب قيمة (K-distance(A: 

إنّ النقطتين B و C هما أقرب نقطتين إلى النقطة A، وبُعد النقطة C عن A هو أكبر لذلك تكون قيمة (K-distance(A  تساوي 2.

• حساب قيمة (K-distance(B: 

إنّ النقطتين A و C هما أقرب نقطتين إلى النقطة B و النقطتان  C  و A لهما نفس البُعد عن B لذلك تكون قيمة (K-distance(B  تساوي 1.

• حساب قيمة (K-distance(C: 

إنّ النقطتين A و B هما أقرب نقطتين إلى النقطة C وبُعد النقطة A  عن B هو الأكبر لذلك تكون قيمة (K-distance(C  تساوي 2.

• حساب قيمة (K-distance(D: 

إنّ النقطتين A و C هما أقرب نقطتين إلى النقطة D والنقطتان A و C  لهما نفس البُعد عن D لذلك تكون قيمة (K-distance(D  تساوي 3.

الآن نقوم بإيجاد قيم الجيران N_k(x_i) من أجل كلّ نقطة:

• K-neighborhood (A) = {B,C} , ||N₂(A)|| =2
• K-neighborhood (B) = {A,C}, ||N₂(B)|| =2
• K-neighborhood (C)= {B,A}, ||N₂(C)|| =2
• K-neighborhood (D) = {A,C}, ||N₂(D)|| =2

الآن سوف نقوم بحساب كثافة مسافة الوصول المحلية LRD لكلّ نقطة، حيث سيتمّ استخدام قيم المسافة-K والمسافة بين كلّ زوج من النقاط و N_k(x_i) من أجل حساب كثافة قابلية الوصول المحلية.

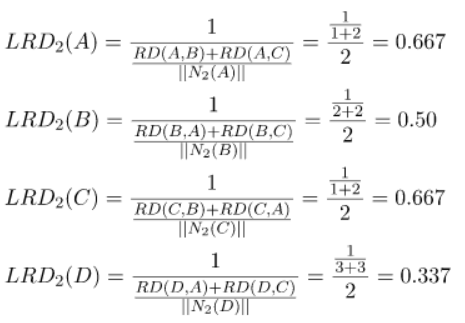
أخيراً سوف نقوم بحساب عامل القيم المتطرفة المحلية لكلّ نقطة، وسوف يتمّ استخدام قيم كثافة قابليّة الوصول المحليّة (LRD) لحساب عامل القيم المتطرفة المحلية LOF.

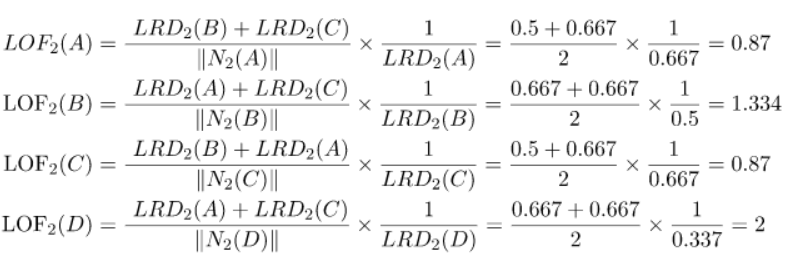
أعلى قيمة لمعامل القيم المتطرفة المحلية LOF بين النقاط الأربع هو (LOF(D، لذلك القيمة D تعتبر قيمة متطرفة. 

محاسن خوارزميّة معامل القيم المتطرفة

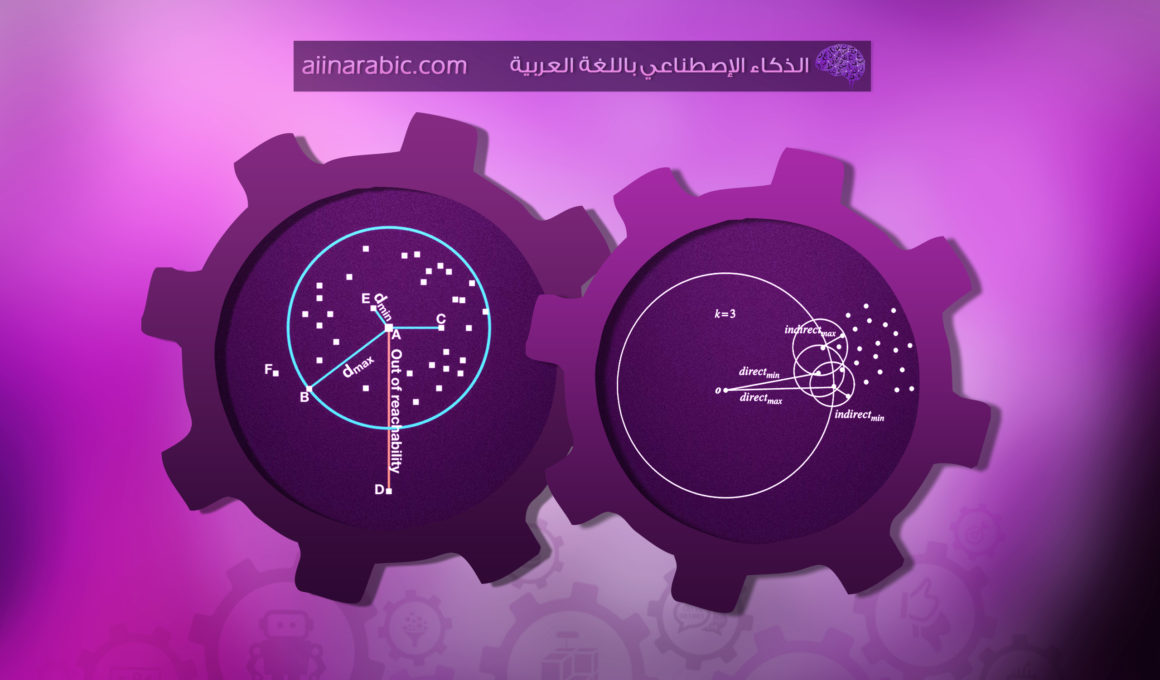
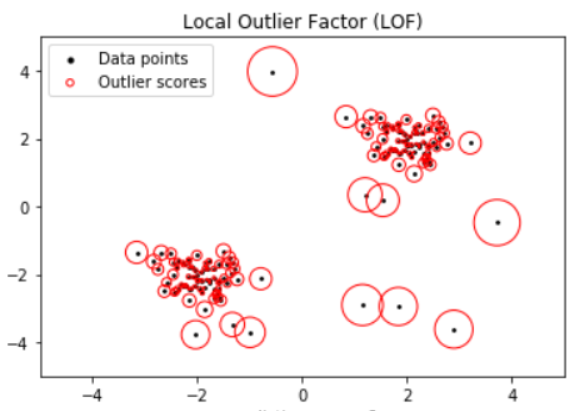
تعتبر النقطة متطرفة  إذا كانت على مسافة صغيرة من حدود كتلة كثيفة للغاية، وقد لا يَعتبر النهج شامل Global Anomaly هذه النقطة بمثابة نقطة متطرفة  outlier (كما يوضح الشكل التالي)، لكن خوارزميّة معامل القيم المتطرفة المحلية LOF بإمكانها تحديد القيم المتطرفة المحلية بشكلٍٍ فعال جداً.

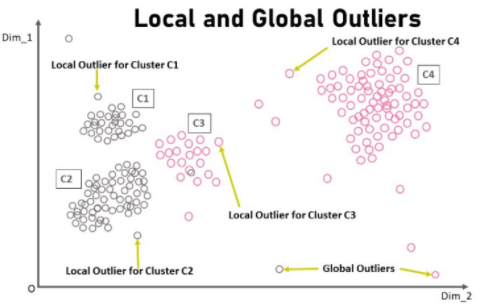
وأحد محاسن هذه الخوارزمية أيضاً أنها تعمل بشكلٍ جيّد عندما تكون البيانات في مجموعة البيانات مختلفة في الكثافة.

مساوئ خوارزميّة اكتشاف القيم المتطرفة المحلية

نظرًا لأنّ معامل القيم المتطرفة المحلية LOF عبارة عن نسبة، فمن الصعب تفسيرها. لا توجد قيمة عتبة Threshold محدّدة حيث يتمّ تعريف النقاط التي تتجاوزها على أنها نقاط متطرفة  outlier، لذلك تحديد القيم المتطرفة outlier يعتمد على المشكلة والمستخدم.

التطبيق العمليّ 

الآن في هذا القسم سنقوم بإجراء تطبيق برمجيّ للخوارزميّة LOF للكشف عن الحالات الشاذّة باستخدام لغة البرمجة بايثون. توفر مكتبة تعلّم الآلة Scikit-Learn ضمن لغة البرمجة بايثون تحقيقًا برمجيًّا لهذه الخوارزميّة لذا سوف نقوم بالاستعانة بهذه المكتبة. 

# data preparation
import pandas as pd
import numpy as np
# data visualzation
import matplotlib.pyplot as plt
# outlier/anomaly detection
from sklearn.neighbors import LocalOutlierFactor

بالإضافة إلى مكتبة تعلّم الآلة قمنا باستدعاء المكتبات التالية :

1. مكتبة Matplotlib هي مكتبة رسوميّة للغة البرمجة بايثون، تحتوي هذه المكتبة على مجموعة من الأدوات تساعد على توليد الرّسوم البيانيّة والأشكال.
2. مكتبةُ بايثون العدديَّة numpy  تحتوي العديد من التوابع الضروريّة للتعامل مع المصفوفات. 
3. مكتبة بانداس Pandas من أجل التّعامل مع مجموعة البيانات.

لنقم الآن بإنشاء مجموعة بيانات تحتوي على خمس نقاط فقط.

# data
df = pd.DataFrame(np.array([[0,1], [1,1], [1,2], [2,2], [5,6]]), columns = ["x", "y"], index = [0,1,2,3,4])

بعد إنشاء مجموعة البيانات لنقم الآن بإجراء عرض لمجموعة البيانات ونرى كيف تتوزّع النقاط.

# plot data points
plt.scatter(df["x"], df["y"], color = "b", s = 65)
plt.grid()

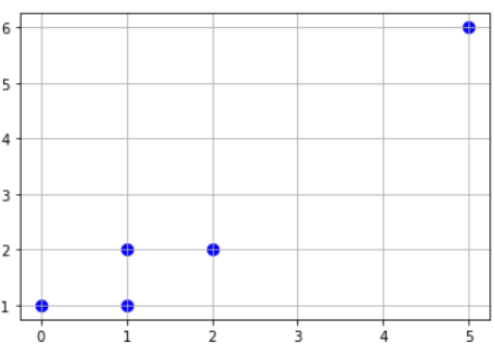
من الشكل 8 نلاحظ أنه بالنظر فقط بإمكاننا تحديد النقطة المتطرفة التي تنحرف بشكلٍ كبير عن بقية النقاط الأخرى، لكنّ هذا الأمر غير ممكن في حال كانت مجموعة البيانات كبيرة، لذلك دعنا نتابع الكشف عن النقطة المتطرفة باستخدام خوارزميّة  اكتشاف القيم المتطرفة المحلية لنرى ما إذا كانت الخوارزميّة قادرة على اكتشافها.

لنقم الآن ببناء نموذج لخوارزميّة Local Outlier Factor باستخدام مكتبة تعلّم الآلة.

# model specification
model1 = LocalOutlierFactor(n_neighbors = 2, metric = "manhattan", contamination = 0.02)

حيث قمنا بتهيئة عدد الجيران بالقيمة 2 وحدّدنا مقياس مانهاتن من أجل قياس المسافة بين النقاط، كما قمنا بتحديد نسبة النقاط المتطرفة contamination في مجموعة البيانات بالنسبة 0.02 

الآن نقوم بإجراء ملاءمة للنموذج على مجموعة البيانات، ومن ثمّ التنبؤ بالقيم المتطرفة حيث يكون خرج النموذج -1 في حال كانت النقطة متطرفة، و 1 في حال كانت النقطة طبيعيّة.

# model fitting
y_pred = model1.fit_predict(df)

نقوم الآن باستخراج دليل النقاط الشاذّة في مجموعة البيانات.

# filter outlier index
outlier_index = np.where(y_pred == -1) # negative values are outliers and positives inliers

أخيراً نقوم بإجراء عرض لمجموعة البيانات وتحديد النقاط الشاذّة منها والطبيعيّة.

# filter outlier values
outlier_values = df.iloc[outlier_index]
# plot data
plt.scatter(df["x"], df["y"], color = "b", s = 65)
# plot outlier values
plt.scatter(outlier_values["x"], outlier_values["y"], color = "r")

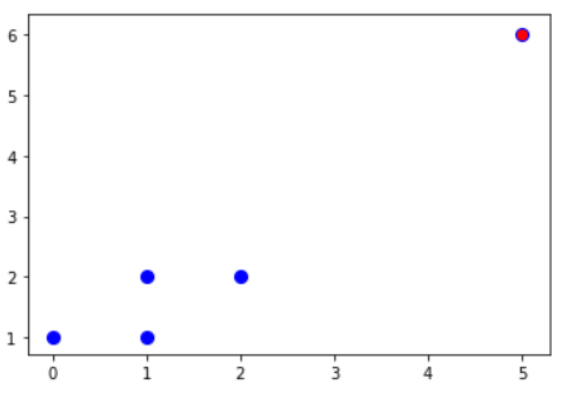
عزيزي القارئ: لمتابعة الشفرة البرمجية كاملة يمكنك الرجوع إلى مستودع الجت هب.

الخاتمة

تعرّفنا في هذا المقال على أحد الخوارزميّات المستخدمة في الكشف عن الحالات الشاذّة، وذلك بناءً على كثافة الجوار ففي حال كانت الكثافة بجوار النقطة عالية ستكون النقطة طبيعيّة ولا تثير أيّ شكوك، و عكس ذلك في حال كانت الكثافة منخفضة فعلى الأرجح أنّ هذه النقطة تسلك سلوكًا مختلفًا عن باقي النقاط في مجموعة البيانات. كما وضّحنا في هذا المقال آليّة عمل هذه الخوارزمية من خلال مثال عمليّ، ومن ثم قمنا بإجراء تطبيق برمجيّ للخوارزميّة بلغة البرمجة بايثون.

المصادر

1.  M. Rezapour, “Anomaly detection using unsupervised methods: credit card fraud case study,” Int J Adv Comput Sci Appl, vol. 10, no. 11, 2019.Rehman. A, Abbas. N, Saba. T, Rahman. S. et al. (September 2018). Classification of acute lymphoblastic leukemia using deep learning. Microscopy Research and Technique.
2.  Mishra, Sanju, et al. “Swarm intelligence in anomaly detection systems: an overview.” International Journal of Computers and Applications 43.2 (2021): 109-118. Deep Learning with python. 
3.  S.-C. Yip, W.-N. Tan, C. Tan, M.-T. Gan, and K. Wong, “An anomaly detection framework for identifying energy theft and defective meters in smart grids,” International Journal of Electrical Power & Energy Systems, vol. 101, pp. 189–203, 2018.
4.  Local Outlier Factor: A way to Detect Outliers.
5.  Local Outlier Factor (LOF) — Algorithm for outlier identification.
6.  Anomaly detection with Local Outlier Factor (LOF).