المَحتويَات
- المقدّمة Introduction
- خوارزميّة التجميع بالمتوسّطات (K-Means Clustering)
- خطوات الخوارزميّة Algorithm Steps
- إيجابيات الخوارزمية
- سلبيات الخوارزمية
- مثال تطبيقي Implementation
- خوارزميّة التجميع بالمتوسّط المتحوّل (Mean-Shift)
- خطوات الخوارزميّة Algorithm Steps
- مثال تطبيقي Implementation
- خوارزميّة التجميع دي بي سكان (DBSCAN) Density-Based Spatial Clustering of Applications
- خطوات الخوارزميّة Algorithm Step
- مثال تطبيقي Implementation
- خوارزميّة التجميع بتعظيم القيمة المتوقعة باستخدام نموذج غاوس المختلط
- Expectation–Maximization (EM) Clustering using Gaussian Mixture Models (GMM)
- خطوات الخوارزميّة Algorithm Steps
- مثال تطبيقي Implementation
- خوارزميّة التجميع الهرميّة (Agglomerative Hierarchical)
- خطوات الخوارزمية Algorithm steps
المقدّمة Introduction
خوارزميّات التجميع Clustering من أكثر الخوارزميّات استعمالاً في تعلم الآلة (Machine Learning) تحت تصنيف التعلّم دون إشراف (Unsupervised Learning)، وهو أسلوب شائع لتحليل البيانات الإحصائيّة المستخدمة في العديد من المجالات.
تعمل خوارزميّات التجميع على تصنيف نقاط البيانات المتشابهة إلى مجموعات محدّدة (Clusters). حيث أنّ نقاط البيانات المصنّفة بنفس المجموعة لها خصائص أو ميّزات متشابهة، بينما نقاط البيانات المصنّفة في مجموعات مختلفة لها خصائص أو ميّزات مختلفة للغاية.
وفي هذه المقالة سوف نتعرّف على خمس خوارزميّات تجميع، والتي تعدّ الأكثر استعمالاً بين علماء البيانات، وسوف نتطرّق إلى الإيجابيّات والسلبيّات لكلّ خوارزميّة.
خوارزميّة التجميع بالمتوسّطات (K-Means Clustering)
من أكثر خوارزميّات التجميع المعروفة بين علماء البيانات، وتُقدّم في كثير من المحاضرات المتعلقة بعلوم البيانات لسهولة فهمها وتطبيقها. لننظر إلى الشكل(1) أدناه للتوضيح .

خطوات الخوارزميّة Algorithm Steps
- في البداية سنقوم يدويّاً باختيار عدد المجموعات المتوقعة (N)، ثمّ ستقوم الخوارزميّة بتحديد النقاط المركزيّة لكلّ مجموعة بشكل عشوائيّ. ولمعرفة عدد المجموعات (N)، سنقوم بصريّاً بإلقاء نظرة سريعة على البيانات وتوقع عدد المجموعات المحتملة والمتميّزة عن بعض. و النقاط المركزيّة هي متجهات لها نفس طول كلّ متجه من متجهات نقاط البيانات وهي (X) في الشكل(1) أعلاه، وهنا نجد أنّ N=3.
- و لتصنيف انتماء أيّ نقطة بيانات لمجموعة محدّدة، سيتمّ حساب المسافة بين تلك النقطة ومركز كلّ مجموعة (X)، ومن ثمّ تصنيف النقطة لتكون في المجموعة التي يكون مركزها (X) الأقرب (الأصغر مسافة) لتلك النقطة.
- وعندما ننتهي من تصنيف جميع النقاط، سنقوم بتغيير مواقع مراكز المجموعات (X) عن طريق إعادة حساب مركز كلّ مجموعة، بأخذ متوسّط (mean) قيمة جميع متّجهات النقاط التي صُنّفت مؤخراً في تلك المجموعة.
- أخيراً سنقوم بتكرار الخطوات الثلاث الأولى لعدد معين من المرّات حتى نحصل على نتيجة مقنعة، أو حتى لا نجد أيّ تغيير ملحوظ لمراكز المجموعات (X).
إيجابيات الخوارزمية
من مميّزات خوارزميّة التجميع بالمتوسطات (K-Means) أنها سريعة جدّاً، لقلة الحسابات المستخدمة لتحديد المجموعات ومراكزها، حيث أنّ تعقيد الخوارزميّة والوقت المستهلك لكامل العمليّة، تزيد خطّياً بزيادة مجموع عدد النقاط الموجودة في البيانات.
سلبيات الخوارزمية
- إنّ تحديد عدد المجموعات (N) يتمّ يدوياً وبدون مساعدة من الخوارزميّة، لكن من المهم للمستخدم أن تقوم هذه العملية بواسطة الخوارزميّة، لمساعدته على فهم طبيعة البيانات، والحصول على بعض التطلعات.
- الخوارزميّة تقوم بدايةً بتحديد النقاط المركزية (X) بشكل عشوائيّ، مما يؤدّي إلى عدم التناسق وظهور نتائج غير قابلة للإعادة، حيث أننا سوف نحصل على نتائج (مراكز مجموعات) مختلفة في كلّ مرة نقوم بتشغيل الخوارزميّة على نفس البيانات.
وفي الجهة الأخرى، خوارزميّة التجميع بالوسطاء (K-Medians) هي خوارزميّة تجميع تتعلق بخوارزميّة التجميع بالمتوسطات (K-Means)، لكن بدلاً من إعادة حساب نقطة مركز المجموعة باستخدام المتوسط (mean) سنستخدم الوسيط (Median) للمجموعة (K-Medians) حيث يعتبر أقلّ حساسيّة تجاه القيم الشاذّة (Outliers)، بسبب استخدام الوسيط ولكنها أبطأ بكثير من خوارزميّة التجميع (K-Means).
ملاحظة: لمن يفضل الإطلاع على المفاهيم الرياضية اضغط هنا
مثال تطبيقي Implementation
خوارزمية التجميع بالمتوسطات#
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import KMeans
from matplotlib import pyplot
تحديد مجموعة البيانات#
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
تحديد النموذج#
model = KMeans(n_clusters=2)
ملائمة النموذج#
model.fit(X)
تخصيص مجموعة لكل مثال#
yhat = model.predict(X)
استرجاع المجموعات الفريدة#
clusters = unique(yhat)
إنشاء مخطط التبعثر لعينات من كل مجموعة#
for cluster in clusters:
الحصول على فهارس الصف للعينات مع هذه المجموعة#
row_ix = where(yhat == cluster)
إنشاء مخطط التبعثر من هذه العينات#
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
إظهار المخطط#
pyplot.show()
يهدف هذا المثال إلى توضيح الظروف التي ستنتج فيها k-means عناقيد غير بديهية وربما غير متوقعة حيث أولا سنعمل على إستيراد المكتبات و البيانات -مكتبات بايثون- الضرورية ومن ثم يتم تحديد مجموعة البيانات وتحديد النموذج ومن ثم يُلاءم هذا النّموذج الموجود في مجموعة بيانات التّدريب، ويتوقع مجموعة لكلّ عينة في مجموعة البيانات. ثمّ يتمّ إنشاء مخطط التّبعثر (Scatter Plot) بنقاط ملوّنة بواسطة المجموعة المخصصة لها.
في هذه الحالة تمّ العثور على تجميع معقول، على الرغم من أنّ التباين غير المتكافئ في كلّ بُعد يجعل الطريقة أقلّ ملاءمة لمجموعة البيانات هذه.
النتيجة:
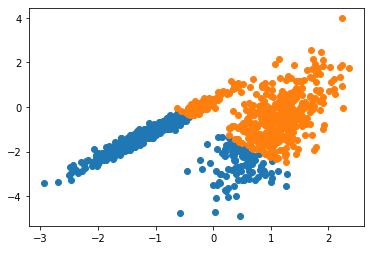
(K-Means)
خوارزميّة التجميع بالمتوسّط المتحوّل (Mean-Shift)
خوارزميّة التجميع بالمتوسط المتحول (Mean-Shift) تعتمد على أسلوب النافذة المنزلقة (Sliding-Window) التي تحاول العثور على المناطق الكثيفة بنقاط البيانات. وهي أيضاً خوارزميّة مركزيّة، بمعنى أنّ الهدف هو تحديد موقع النقاط المركزيّة لكلّ مجموعة من خلال تحديث انزلاق النافذة، وتحديث النقاط التي بداخلها، ومن ثمّ أخذ متوسّطاتها (Mean) كمركز للمجموعة.
وفي حال كان لدينا العديد من النوافذ المرشحة كمركز للمجموعة الواحدة، تتمّ تصفية هذه النوافذ المرشحة في مرحلة ما بعد المعالجة؛ للقضاء على النسخ المكرّرة تقريباً والإبقاء على نافذة واحدة لكلّ مجموعة، وتحديد نقطة المركز عن طريق متوسّط (Mean) النافذة.
فننظر إلى الشكل (3) أدناه للتوضيح:

منزلقة واحدة
خطوات الخوارزميّة Algorithm Steps
- بدايةً للشرح المبسط للخوارزميّة، سننظر في مجموعة من النقاط في الفضاء ثنائيّ الأبعاد، كما في الشكل (3). سنبدأ مع نافذة انزلاق دائريّة الشكل التي تحتوي عدداً من النقاط (C) المختارة عشوائيّاً، ولديها نصف قطر(Radius(rكنواة للنافذة. العمليّة تشبه تسلق التل، كالذي يقوم على تدريج حركة النواة بشكل متكرّر إلى منطقة ذات كثافة أعلى، في كلّ خطوة حتى الوصول إلى التقارب (Convergence).
- في كلّ تكرار يتمّ انتقال النافذة المنزلقة إلى مناطق ذات كثافة أعلى من باقي النقاط، مع انتقال نقطة المركز بحساب المتوسّط لكلّ نافذة منتقلة أو متحوّلة (ومن هنا جاء اسم الخوارزميّة). مع العلم أنّ الكثافة داخل النافذة المنزلقة تتناسب مع عدد النقاط التي بداخلها.
- ستقوم الخوارزميّة بمواصلة انزلاق النافذة، حتى لا يكون هناك أيّ اتجاه آخر يمكن أن يستوعب نافذة جديدة بنقاط أكثر (كثافة أكبر) من النافذة السابقة. نستمرّ في تحريك الدّائرة ومن ثمّ نتوقف عندما لا يمكن للنافذة الجديدة أن تستوعب نقاطاً أكثر (كثافتها أقلّ من السابقة).
- عادة تتمّ هذه العمليّات الثلاث الأولى مع العديد من النوافذ المنزلقة، حتى تقع كافة النقاط داخل نافذة واحدة. أما عندما تتداخل النوافذ المنزلقة تقوم الخوارزميّة على إبقاء النافذة الأعلى كثافة، والتي تحتوي على نقاط أكثر.
- وأخيراً كلّ نقطة بيانات سوف تنتمي لنافذة ما وكل نافذة تقيم في مجموعة خاصة بها.
في الشكل(4)، يوجد توضيح للعملية بأكملها من البداية حتى النهاية، مع نوافذ منزلقة متعدّدة، حيث أنّ النقطة السوداء تمثل مركز كلّ نافذة، والنقاط الرماديّة تمثل نقاط البيانات.

على النّقيض من خوارزمية التجميع (K-Means)، فإن خوارزميّة (Mean-Shift) لا تحتاج لتحديد عدد المجموعات (N) مسبقاً، حيث أنّ الخوارزميّة ستقوم تلقائيّاً بكشف عدد من المجموعات.
إن طريقة عمل الخوارزميّة بتحديد مناطق الكثافة تعتبر ميّزة قوية، حيث أنّها أيضاً بديهيّة الفهم ومتناسبة مع طبيعة توجّه البيانات، لكنّ عمليّة تحديد حجم النافذة أو الدّائرة (r) تعتبر من السلبيّات لأنها تتمّ عشوائيّاً ويدويّاً بدون مساعدة الخوارزميّة.
مثال تطبيقي Implementation
خوارزمية التجميع بالمتوسط المتحول#
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import MeanShift
from matplotlib import pyplot
تحديد مجموعة البيانات#
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
تحديد النموذج#
model = MeanShift()
ملائمة النموذج وتوقع المجموعات#
yhat = model.fit_predict(X)
استرجاع المجموعات الفريدة#
clusters = unique(yhat)
إنشاء مخطط التبعثر لعينات من كل مجموعة#
for cluster in clusters:
الحصول على فهارس الصف للعينات مع هذه المجموعة#
row_ix = where(yhat == cluster)
إنشاء مخطط التبعثر من هذه العينات#
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
إظهار المخطط#
pyplot.show()
يهدف هذا المثال إلى توضيح الظروف التي ستنتج فيها Mean-Shiftعناقيد غير متوقعة حيث أولا سنعمل على استيراد المكتبات و البيانات -مكتبات بايثون- الضرورية ومن ثم يتم تحديد مجموعة البيانات وتحديد النموذج ومن ثم يُلاءم هذا النّموذج الموجود في مجموعة بيانات التّدريب، ويتوقع مجموعة لكلّ عينة في مجموعة البيانات، ثمّ يتمّ إنشاء مخطط التبعثر (Scatter Plot) بنقاط ملوّنة بواسطة المجموعة المخصّصة لها.
في هذه الحالة، توجد مجموعة معقولة من الكتل في البيانات.
النتيجة:
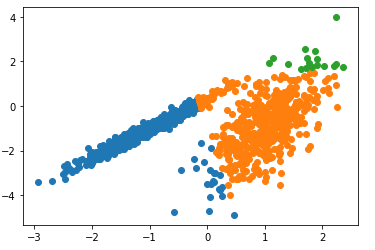
التجميع (Mean-shift)
خوارزميّة التجميع دي بي سكان (DBSCAN) Density-Based Spatial Clustering of Applications
خوارزميّة دي بي سكان (DBSCAN) تعتمد على الكثافة مثل خوارزميّة التجميع بالمتوسّط المتحوّل (Mean-Shift)، ولكن مع وجود ميّزتين إضافيتين بارزتين. ننظر إلى الشكل(6) أدناه:

خطوات الخوارزميّة Algorithm Step
- تعتمد الخوارزميّة على تحديد كلّ نقطة إذا تمت زيارتها أم لا . تبدأ الخوارزميّة مع نقطة بيانات لم تتمّ زيارتها مسبقاً، ثمّ يتمّ استخراج النقاط المجاورة (neighborhood) لهذه النقطة، باستخدام مسافة إبسلون (epsilon ε)، حيث أنّ جميع النقاط التي تقع ضمن مسافة ابسلون ε هي نقاط مجاورة لتلك النقطة.
- إذا كان هناك عدد كافٍ من النقاط المجاورة وفقاً لأدنى حدّ من النقاط (minPoint)، سوف تبدأ عملية التجميع وتصبح نقطة البيانات الحاليّة هي النقطة الأولى في المجموعة الجديدة. وإذا لم يكن هناك عدد كافٍ من النقاط المجاورة، سيتمّ اعتبار هذه النقطة ضوضاء (لاحقاً هذه النقطة المعلّمة كضوضاء قد تصبح جزءاً من المجموعات). لكن في كلتا الحالتين ستقوم الخوارزميّة بتعليم هذه النقطة التي تشكل ضوضاء كنقطة تمت زيارتها.
- بالنسبة للنقطة الأولى في المجموعة الجديدة، جميع النقاط المجاورة لهذه النقطة (التي تكون ضمن نطاق مسافة إبسلون ε) ستكون معها في نفس المجموعة الجديدة. ثمّ تتكرّر هذه الخطوة لجميع النقاط التي أُضيفت مؤخراً في المجموعة.
- وتتكرّر الخطوات الثلاث الأولى لكلّ مجموعة، إلى أن يتمّ تحديد جميع النقاط المجاورة، كنقطة تمت زيارتها للمجموعة الحاليّة.
- بمجرّد الانتهاء من المجموعة الحاليّة (عندما لا نجد نقاطاً إضافيّة مجاورة)، يتمّ البدء مجدّداً من الخطوة الأولى، وعشوائيّاً ستقوم الخوارزميّة بتحديد نقطة جديدة لم يتمّ زيارتها مسبقاً، لمعالجتها واكتشاف إذا كانت بداية لمجموعة جديدة أو مجرّد ضوضاء لا تنتمي لمجموعة جديدة. هذه العملية تتكرّر حتى يتمّ وضع علامة على كافة النقاط الموجودة في البيانات على أنه تمت زيارتها. وفي النهاية ستقوم الخوارزميّة بوسم جميع النقاط، كنقاط منتمية لمجموعة ما أو مجرّد ضوضاء.
خوارزميّة (DBSCAN) تطرح مزايا منافسة مقارنة بخوارزميّات التجميع الأخرى.
أوّلا: لا يتطلب من المستخدم تحديد عدد المجموعات (N) مسبقاً، كما أنها تأخذ القيم الشاذة (Outliers) بعين الاعتبار، على عكس الخوارزميّتين السابقتين، حيث أنّ المتوسّط (Mean) يتأثر بالقيم المتطرّفة حتى لو كانت مختلفة جدّاّ عن المجموعة، أيضاً تتميز الخوارزميّة بقدرتها على تحديد شكل وحجم المجموعات بطريقة جيّدة للغاية.
السلبية الرئيسة لخوارزميّة التجميع دي بي سكان(DBSCAN) هي أنها لا تؤدّي لنتيجة جيدة عندما تكون المجموعات متفاوتة الكثافة؛ وذلك لأنه عندما نحدّد نطاق أو عتبة مسافة إبسلون ε والحدّ الأدنى من النقاط المجاورة (minPoint)، سوف نجد أداءً مختلفاً باختيار النقاط المجاورة من مجموعة إلى مجموعة أخرى عندما تختلف الكثافة بينهم. هذه السلبيّة تحدث أيضاً في البيانات التي تتسم بأبعاد عالية، حيث يصبح تحديد مسافة εابسلون تحدّياً كبيراً.
مثال تطبيقي Implementation
#خوارزميةدي بي سكان
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import DBSCAN
from matplotlib import pyplot
تحديد مجموعة البيانات#
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
تحديد النموذج#
model = DBSCAN(eps=0.30, min_samples=9)
ملائمة النموذج وتوقع المجموعات#
yhat = model.fit_predict(X)
استرجاع المجموعات الفريدة#
clusters = unique(yhat)
إنشاء مخطط التبعثر لعينات من كل مجموعة#
for cluster in clusters:
الحصول على فهارس الصف للعينات مع هذه المجموعة#
row_ix = where(yhat == cluster)
إنشاء مخطط التبعثر من هذه العينات#
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
إظهار المخطط#
pyplot.show()
يهدف هذا المثال إلى توضيح الظروف التي ستنتج فيها خوارزمية التجميع دي بي سكان DBSCAN عناقيد غير بديهية وربما غير متوقعة حيث أولاً سنعمل على استيراد المكتبات و البيانات -مكتبات بايثون- الضرورية ومن ثم يتم تحديد مجموعة البيانات وتحديد النموذج ومن ثم يُلاءم هذا النّموذج الموجود في مجموعة بيانات التّدريب، ويتوقع مجموعة لكلّ عينة في مجموعة البيانات، ثمّ يتمّ إنشاء مخطط التبعثر (Scatter Plot) بنقاط ملوّنة بواسطة المجموعة المخصّصة لها.
في هذه الحالة تمّ العثور على مجموعة معقولة، على الرّغم من الحاجة إلى مزيد من الضبط.
النتيجة:
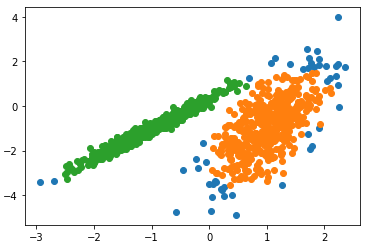
التجميع دي بي سكان
خوارزميّة التجميع بتعظيم القيمة المتوقعة باستخدام نموذج غاوس المختلط
Expectation–Maximization (EM) Clustering using Gaussian Mixture Models (GMM)
إنّ أحد العيوب الرئيسيّة لخوارزميّة التجميع (K-Means)، هو استخدامها البسيط لقيمة متوسّط المجموعة كمركز لها. يمكننا أن نرى أنّ هذه الطّريقة ليست الأفضل للقيام بالتجميع لبعض البيانات، من خلال النّظر إلى الشكل (8).
على الجانب الأيسر يبدو لنا واضحاً تماماً للعين البشريّة، أنّ هناك دائرتين مع أنصاف أقطار مختلفة، حيث نجد أنّ خوارزميّة التجميع بالمتوسطات (K-Means) لا يمكنها التّعامل مع هذا النوع من البيانات، لأنّ القيم المتوسّطة للمجموعتين قريبة جداً من بعضها البعض.
أيضاً في الجانب الأيمن نجد أنّ الخوارزميّة فشلت في تحديد المجموعتين، لأنّ المجموعتان غير متمحورة حول المركز أو الوسط، وهذا الفشل يحدث بسبب استخدام متوسّط المجموعات.

نموذج غاوس المختلط GMMs يعطينا المزيد من المرونة مقارنةً بخوارزميّة التجميع (K-Means). حيث في نموذج غاوس المختلط (GMMs) نفترض أنّ نقاط البيانات تتبَع التوزيع الغاوسيّ (Gaussian Distribution)؛ أي التوزيع الطبيعيّ .
ومع افتراض أنّ البيانات تتبع هذا التوزيع فإنّ القيود المفروضة تقلّ على العكس في خوارزميّة التجميع (K-Means)، نفترض أنّ البيانات دائريّة و متمحورة حول المتوسّط (المركز).
وبهذه الخوارزميّة (GMMs)، لدينا مدخلان لوصف شكل المجموعات: المتوسّط (Mean) والانحراف المعياريّ (Standard Deviation) يمكنك العودة إلى الرابط التالي لمعرفة معنى الانحراف المعياري رياضياً اضغط هنا على سبيل المثال في البيانات ثنائيّة الأبعاد يمكن للمجموعات أن تأخذ أيّ شكل من الأشكال البيضويّة (بما أنه لدينا الانحراف المعياريّ في كل من الاتجاهين X و Y)، وبالتالي يتمّ تعيين كلّ توزيع غاوسيّ (GMM) إلى مجموعة واحدة. لمعرفة ماهو التوزيع الغاوسي اضغط هنا
ومن أجل العثور على مدخلات غاوس لكلّ مجموعة (مثل المتوسّط والانحراف المعياريّ)، سوف نستخدم خوارزميّة تحسين (Optimization Algorithm) تسمى تعظيم القيمة المتوقعة Expectation-Maximization (EM). كما هو مبين في الشكل (9)، يوجد توضيح للتوزيع الغاوسيّ (GMMs) على المجموعتين . بعد ذلك، يمكننا المضيّ قدُماً في عملية التجميع وفق خوارزمية التجميع بتعظيم القيمة المتوقعة(EM) باستخدام نموذج غاوس المختلط (GMMs).

خطوات الخوارزميّة Algorithm Steps
- نبدأ بتحديد عدد المجموعات (N)، وبشكل عشوائيّ سنقوم يدوياً بتحديد مدخلات التوزيع الغاوسيّ لكلّ مجموعة. ويمكننا أيضاً أن نحاول تخمين المدخلات الأوليّة، من خلال إلقاء نظرةٍ سريعة على البيانات. لكن ليس من الضروريّ محاولة إيجاد المدخلات عن طريق النظر للبيانات، كما نرى في الشكل(9) بدأ التوزيع بشكلٍ ضعيف جدّاً، ثمّ تحسنت النتائج بشكلٍ سريع من خلال التكرار.
- بناءً على توزيعات غاوسي المعطاة لكلّ مجموعة، ستقوم الخوارزميّة بحساب احتماليّة انتماء كلّ نقطة بيانات إلى توزيع أو مجموعة معينة. كلما كانت النقطة أقرب إلى مركز(متوسّط) التوزيع الغاوسيّ للمجموعة الواحدة، كلما كان من المرجح أن تنتمي إلى تلك المجموعة (التوزيع)، وهذا أمر بديهيّ بما أننا نفترض أنّ أغلب البيانات في المجموعة قريبة من مركز المجموعة.
- استناداّ إلى هذه الاحتمالات، ستقوم الخوارزميّة بتحديث حسابات جديدة من المدخلات لتوزيعات غاوس لكلّ مجموعة، حيث أنها تقوم بأقصى زيادة لاحتماليّة انتماء النقاط لتوزيع أو مجموعة معينة.
- يتمّ إعادة الخطوة الثانية والثالثة بشكلٍ متكرّر حتى الوصول إلى حالة التقارب، حيث أنه مهما قمنا بتكرار الخطوات لا تتغير التوزيعات بشكلٍ ملحوظ.
يتمّ حساب هذه المدخلات الجديدة عن طريق استخدام الجمع الموزون (Weighted Sum) لأماكن نقاط البيانات، حيث أنّ وزن كلّ نقطة يشير إلى مدى احتماليّة انتمائها لمجموعة معينة. لشرح العمليّة بشكلٍ أفضل ، نجد في الشكل(9) وعلى وجه الخصوص سنأخذ المجموعة الصفراء كمثال، نرى أنّ التوزيع يبدأ للمجموعة الصفراء بشكل عشوائيّ في التكرار الأوّل، ونلاحظ أنّ معظم النقاط الصفراء تقع يمين أعلى المجموعة أو التوزيع، وعندما نقوم بحساب وزن احتماليّة انتماء النقاط الصفراء للمجموعة نجد أنها أقرب للمجموعة الصفراء من المجموعة البرتقالية، لكن بالرغم من ذلك أغلب النقاط هي بعيدة من جهة اليمين. وبالتالي بطبيعة الحال، في التكرارات الأخرى سوف يتمّ تحديث وتحويل متوسط التوزيع أو المجموعة الجديد بشكلٍ أقرب إلى النقاط الواقعة يمين التوزيع التوزيع
يمكننا أيضاً ملاحظة أنّ معظم النقاط التابعة للمجموعة الصفراء هي “من أعلى اليمين إلى أسفل اليسار”، ولذلك يتغير الانحراف المعياريّ لإنشاء مجموعة بيضويّة أكثر تناسباً لاتجاه وتوزيع هذه النقاط، مما يؤدّي إلى الوصول إلى أقصى زيادة لاحتماليّة انتماء النقاط لمجموعتها الصفراء، عن طريق القرب من مركزها الحقيقيّ.
تتميز هذه الخوارزميّة بنقطتين:
- أوّلاً، خوارزميّة نموذج غاوس المختلط (GMMs) أكثر مرونة من خوارزميّة التجميع (K-Means) من حيث التغاير المجموعيّ (Cluster Covariance)، وذلك بسبب مدخل الانحراف المعياريّ، وهذا ما يمكّن الخوارزمية أن تميز المجموعات التي تكون على أي شكل بيضويّ، أو شكل ناقص غير دائريّ. خوارزميّة التجميع (K-Means) هي في الواقع حالة خاصة لخوارزميّة نموذج غاوس المختلط (GMM)، حيث إنّ تغاير أو تباين كلّ مجموعة من خلال كلّ الأبعاد يساوي صفراً.
- ثانياَ، بما أنّ خوارزميّة نموذج غاوس المختلط (GMMs) تستخدم أسلوب الاحتمالات، من الممكن أن تصنَّف نقطة البيانات الواحدة ضمن أكثر من مجموعة في نفس الوقت. لذلك إذا كانت النّقطة مرجحة بأن تنتمي لمجموعتين، نستطيع ببساطة أن نصنفها لكلّ فئة بناءً على احتماليّة وجودها في تلك الفئة، على سبيل المثال: نقطة البيانات تنتمي بنسبة X للمجموعة الأولى؛ بمعنى آخر (GMMs) تدعم الاختلاط ومن هنا جاءت التسمية.
مثال تطبيقي Implementation
خوارزمية التجميع بالقيمة المتوقعة باستخدام نموذج غاوس المختلط#
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.mixture import GaussianMixture
from matplotlib import pyplot
تحديد مجموعة البيانات#
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
تحديد النموذج#
model = GaussianMixture(n_components=2)
ملائمة النموذج#
model.fit(X)
تخصيص مجموعة لكل مثال#
yhat = model.predict(X)
استرجاع المجموعات الفريدة#
clusters = unique(yhat)
إنشاء مخطط التبعثر للعينات من كل مجموعة#
for cluster in clusters:
الحصول على فهارس الصف للعينات مع هذه المجموعة#
row_ix = where(yhat == cluster)
إنشاء مخطط التبعثر من هذه العينات#
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
إظهار المخطط#
pyplot.show()
يهدف هذا المثال إلى توضيح الظروف التي ستنتج فيها القيمة المتوقعة باستخدام نموذج غاوس EM with GMMعناقيد غير متوقعة حيث أولا سنعمل على إستيراد المكتبات و البيانات -مكتبات بايثون- الضرورية ومن ثم يتم تحديد مجموعة البيانات وتحديد النموذج ومن ثم يُلاءم هذا النّموذج الموجود في مجموعة بيانات التّدريب، ويتوقع مجموعة لكلّ عينة في مجموعة البيانات، ثمّ يتمّ إنشاء مخطط التبعثر (Scatter Plot) بنقاط ملوّنة بواسطة المجموعة المخصصة لها. في هذه الحالة يمكننا أن نرى أنه تمّ تحديد المجموعات بشكل مثاليّ، هذا ليس مفاجئًا نظرًا لأنّ مجموعة البيانات تمّ إنشاؤها كمزيج باستخدام نموذج غاوس المختلط.
النتيجة:
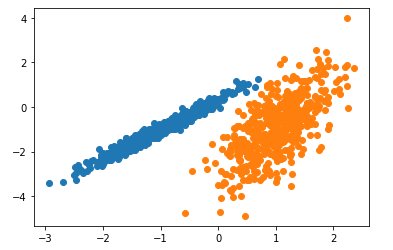
التجميع GMM
خوارزميّة التجميع الهرميّة (Agglomerative Hierarchical)
بشكل عام، خوارزميّات التجميع الهرميّة تنقسم إلى فئتين:
- التجميع الهرميّ من الأعلى إلى الأسفل (Divisive Clustering)
- التجميع الهرميّ من الأسفل إلى الأعلى (Agglomerative Hierarchical).
سنقوم بالحديث عن خوارزميّة التجميع من الأسفل إلى الأعلى، تقوم هذه الخوارزميّة بالبداية بمعاملة كلّ نقطة بيانات كمجموعة مستقلة بذاتها، ومن ثمّ تبدأ بالتدريج بدمج أزواج من نقاط البيانات المتشابهة مكوِّنة مجموعات جديدة، تستمرّ العملية حتى يتمّ دمج كلّ المجموعات تحت مجموعة واحدة، وبالتالي يطلق على التجميع الهرميّ من الأسفل إلى الأعلى بالتكتل الهرميّ (Agglomerative Hierarchical).
يتمّ تمثيل هذا التسلسل الهرميّ كشجرة أو (Dendrogram). حيث أنّ جذر الشجرة هو مجموعة فريدة من نوعها تجمع كلّ نقاط البيانات، وأوراق الشجرة تمثل هذه النقاط كمجموعات فرديّة (من نقطة واحدة فقط). ننظر إلى الشكل (11) قبل الانتقال إلى شرح خطوات الخوارزميّة:

خطوات الخوارزمية Algorithm steps
- نبدأ بالتعامل مع كلّ نقطة بيانات فرديّة كمجموعة بحدّ ذاتها، أي إذا كان لدينا عدد من نقاط البيانات تساوي X، سوف نحصل في البداية على عدد مجموعات (N) تساوي X. لاحقاً سنقوم بقياس المسافة بين المجموعات الفرديّة، يوجد عدّة مقاييس للمسافة من الممكن استخدامها مع التجميع الهرميّ، على سبيل المثال سنستخدم متوسّط الربط (Average Linkage) الذي يحدّد المسافة بين مجموعتين، لتكون المسافة المحسوبة هي متوسّط المسافة بين نقاط البيانات في المجموعة الأولى، ونقاط البيانات في المجموعة الثانية.
- في كلّ مرحلة تكرار نقوم تدريجيّاً بدمج مجموعتين في مجموعة واحدة، ويتمّ اختيار المجموعتين اللتين سيتمّ دمجهما بناءً على المجموعتين ذات المسافة الأقصر (أصغر قيمة لمتوسّط الربط)، أي وفقاً لقصر المسافة تعتبر المجموعتان المزدوجتان أكثر تشابهاّ.
- يتمّ تكرار الخطوة 2 حتى نصل إلى جذر الشجرة، أي يصبح لدينا مجموعة أو كتلة واحدة فقط والتي تحتوي على جميع نقاط البيانات. وفي النهاية يمكننا اختيار عدد المجموعات (N) التي نريدها ببساطة، وذلك بتحديد متى نتوقف عن الجمع بين المجموعات، أي عندما نتوقف عن بناء الشجرة ونقوم بقطعها (Tree-cut-off).
لا يتطلب التجميع الهرميّ تحديد عدد المجموعات (N) مسبقاً، حيث يمكننا تحديد عدد المجموعات لاحقاً بناءً على المجموعات التي تبدو أفضل بصريّاً عند قطع الشجرة بعد بنائها. بالإضافة إلى أنّ الخوارزميّة غير حساسة لاختيار نوع مقياس المسافة (Distance Measure)، كلّ مقياس يعمل بشكل جيد ويعطي نفس النتائج بشكل تقريبيّ، على العكس من باقي الخوارزميّات تتأثر بشكل كبير وتعطي نتائج مختلفة تماماً عند اختلاف مقياس المسافة المستخدم، واختيارها أمر في بالغ الأهمية.
وعمليّاً من الأمثل استخدام التجميع الهرميّ في حالة معرفتنا السابقة بوجود تسلسل هرميّ للبيانات، وكنا نرغب من الخوارزمية أن تكشف لنا النمط الهرميّّ بين البيانات، وهذا لا يمكن الوصول له باستخدام الخوارزميّات الأخرى.
أمّا السلبيّات، فإنّ عملية التسلسل الهرميّ منخفضة الكفاءة مقارنة بباقي الخوارزميّات، نظراً لزيادة التعقيد الخطيّ والوقت المستهلك لبناء المجموعات، حيث إنها تزيد بشكل أُسّي (O(n³على عكس التعقيد الخطيّ لخوارزميّة التجميع (K-Means) و خوارزمية نموذج غاوس المختلط (GMM).
مثال عمليّ:
خوارزمية التجميع الهرمية#
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import AgglomerativeClustering
from matplotlib import pyplot
تحديد مجموعة البيانات#
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4)
تحديد النموذج#
model = AgglomerativeClustering(n_clusters=2)
ملائمة النموذج وتوقع المجموعات#
yhat = model.fit_predict(X)
استرجاع المجموعات الفريدة#
clusters = unique(yhat)
إنشاء مخطط التبعثر لعينات من كل مجموعة#
for cluster in clusters:
الحصول على فهارس الصف للعينات مع هذه المجموعة#
row_ix = where(yhat == cluster)
إنشاء مخطط التبعثر من هذه العينات#
pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
إظهار المخطط#
pyplot.show()
يهدف هذا المثال إلى توضيح الظروف التي ستنتج فيها Agglomerative Hierarchical عناقيد غير متوقعة حيث أولا سنعمل على إستيراد المكتبات و البيانات -مكتبات بايثون- الضرورية ومن ثم يتم تحديد مجموعة البيانات وتحديد النموذج ومن ثم يُلاءم هذا النّموذج الموجود في مجموعة بيانات التّدريب، ويتوقع مجموعة لكلّ عينة في مجموعة البيانات، ثمّ يتمّ إنشاء مخطط التبعثر (Scatter Plot) بنقاط ملوّنة بواسطة المجموعة المخصصة لها.
في هذه الحالة ، تمّ العثور على مجموعة معقولة.
النتيجة:

الهرمية (Agglomerative Hierarchical)
الخاتمة :
نلاحظ من خلال خوارزميات التجميع يمكننا استنباط بعض الرؤى القيمة، من خلال معرفة ما هي المجموعات المحتملة التي تقع فيها نقاط البيانات.
وفي هذه المقالة تعرفنا على خمس خوارزميات تجميع، والتي تعد الأكثر استعمالاً بين علماء البيانات، و تطرقنا إلى الإيجابيات أو السلبيات لكل خوارزمية.
سوف ننهي المقال بعرض صورة رائعة توضح أداء الخوارزميات المذكورة في هذا المقال على مجموعة من أشكال البيانات المختلفة.

المراجع:
- https://machinelearningmastery.com/clustering-algorithms-with-python/
- https://www.freecodecamp.org/news/8-clustering-algorithms-in-machine-learning-that-all-data-scientists-should-know
- https://www.kdnuggets.com/2018/06/5-clustering-algorithms-data-scientists-need-know.html
- https://scikit-learn.org/stable/modules/clustering.html
- https://towardsdatascience.com/the-5-clustering-algorithms-data-scientists-need-to-know-a36d136ef68




تعليقان
مقال مبسط و واضح. انصح باضافة طرق تقييم جودة ال clustering الى المقال او في مقالات اخرى قادمة و اضافة مجالات التطبيق المرتبطة بكل نوع.
بالتوفيق
سنعمل على ذلك بالتأكيد ….
شكرا لاهتمامكم