التدّقيق العلمي: د. م. دانيا الصّغير، م. رامي عقّاد
التدّقيق اللّغوي: هبة الله فلّاحة
المَحتويَات
المقدمة:
تعتبر خوارزميّة التّوقّع الخطّيّ من أساسيّات مجال تعلّم الآلة، وسنتعرّف في هذا المقال على سبب استخدامها ومبدأ عملها و كيفيّة تطبيقها من خلال التّوابع الرّياضيّة الخاصّة بها وكيفيّة الوصول لأفضل النّتائج من خلالها.
ما هي خوارزميّة التّوقّع الخطّيّ Linear Regression ؟
هي خوارزميّة تعرف علاقة خطّيّة بين متغيّر مستقلّ ومتغيّر تابع، بهدف التنبّؤ بنتيجة الأحداث المستقبليّة.
وهي خوارزميّة تعلّم بالإشراف Supervised Learning تحاكي العلاقة الرّياضيّة بين المتغيّرات، وتضع تنبّؤات للمتغيّرات المستمرّة أو الرّقميّة مثل المبيعات أو الرّاتب أو العمر أوسعر المنتج، وغيرها.
ملاحظة : سنتناول في هذا المقال التّوقّع الخطّيّ لمتغيّر واحد فقط .
يتمّ تمثيل التّوقّع الخطّيّ بالتّابع :
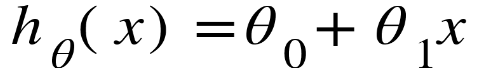
حيث أنّ :
عوامل المعادلة: θ0و θ1
عيّنة من البيانات: x
النّتيجة المتوقّعة :hθ(x)
في أيّ مسألة توقّع خطّيّ يكون هدفنا بسيطًا:
بالنّظر إلى مجموعة التّدريب، نريد أن تتعلّم الدّالة h: x → y بحيث تكون (h (x توقعًا جيدًّا مقابل القيمة الفعليّة y (أفضل علاقة خطّيّة ممكنة) كما هو موضّح في الشّكل التّالي:
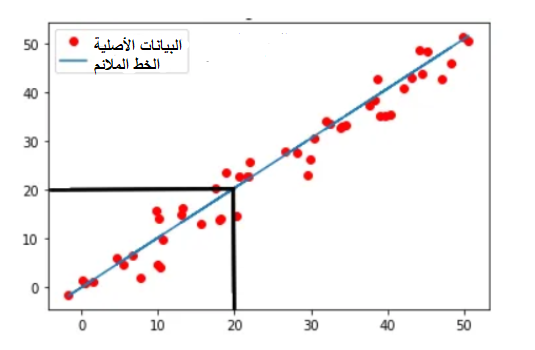
ولكن كيف نحدّد قيمة العوامل θ0 و θ1 بحيث تحقّق أفضل علاقة خطّيّة best fit والملاءمة الأفضل ؟ الجواب أنّه علينا الاستعانة بتابع التّكلفة.
تابع التّكلفة cost function:
يقيس أداء نموذج تعلّم الآلة Machine Learning Model المدرّب على بيانات معيّنة؛ من خلال حساب الخطأ بين القيم المتوقّعة والقيم الفعليّة وتقدّم هذا الخطأ على شكل رقم حقيقيّ واحد.
يتمّ تمثيل تابع التّكلفة بالتّابع الرّياضيّ التّالي:
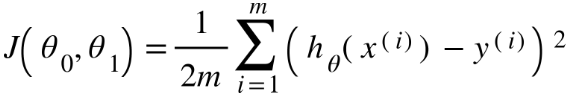
m : عدد عيّنات البيانات
h(x) :القيمة المتوقّعة
y : القيمة الحقيقيّة
i : رقم العيّنة
هدفنا هو اختيار قيم العوامل θ0 و θ1 التي تحقّق أقلّ خطأ أي أقل تكلفة؛ وهذا ما يعبّر عنه بتصغير قيمة التّكلفة minimize cost function وبهذا تكون القيمة المتوقّعة أقرب ما يمكن للقيمة الفعليّة.
لكن لماذا تصغير قيمة التّكلفة يحقّق علاقة خطّيّة أفضل ؟
من معادلة تابع التّكلفة من الواضح تمامًا أنّ تابع التّكلفة J ( θ0, θ1) يتناسب طرديًّا مع مربّع الفرق بين توقّعنا أي h (x) والقيمة الحقيقيّة y. نظرًا لأنّنا نريد أن تكون تنبّؤاتنا قريبة جدًّا أو مساوية للقيم الحقيقيّة، فمن الواضح أنّنا سنحتاج إلى أن يكون الفرق بين الاثنين صغيرًا قدر الإمكان، وبالتّالي يجب علينا تصغير قيمة الخطأ أو تصغير التّكلفة.
؟ولكن كيف سنتوقع قيم المعاملات التي ستعطي العلاقة الخطّيّة الملاءمة للبيانات بأفضل ما يكون
نقوم بتصغير قيمة التّكلفة ولكن كيف؟ من خلال الانحدار التّدريجيّ
حيث أنّه أثناء تدريب النّموذج يتمّ تعديل قيم العوامل θ0, θ1 بشكل متكرّر حتّى الوصول إلى القيم المناسبة التي ستعطي العلاقة الخطّيّة الملاءمة للبيانات best fit.
الانحدار التّدريجيّ gradient descent:
هو خوارزميّة تحسين تكراريّة تستخدم للعثور على حدّ أدنى محليّ Local minimum لوظيفة معيّنة، تُستخدم هذه الطّريقة بشكل شائع في مجال تعلّم الآلة (ML) وتقوم بتعديل العوامل بشكل متكرّر لتصغير قيمة التّكلفة.
لاحقًا سنقوم بتطبيق الانحدار التّدريجيّ للعوامل θ0, θ1 للوصول إلى القيم المثاليّة؛ من أجل تحقيق أدنى تكلفة وإيجاد أفضل توقّع خطّيّ للبيانات.
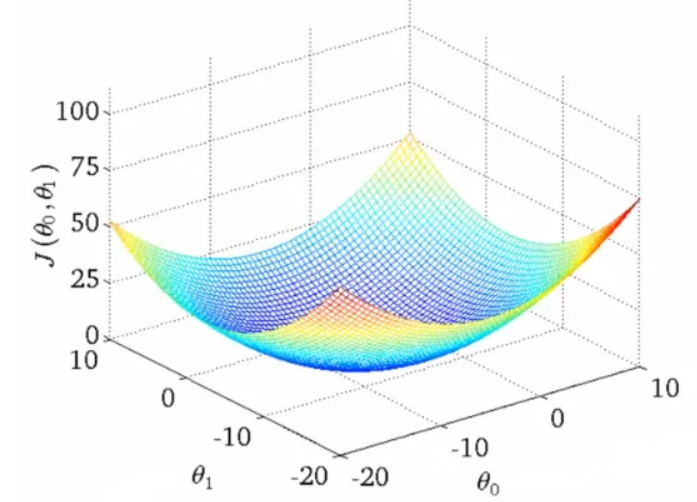
وننوّه أنّه يجب مراقبة دالة التّكلفة مع كلّ خطوة من الانحدار التّدريجيّ، لنعرف متى نقترب أكثر من القيم المثاليّة.
ويعبّر عن الانحدار التّدريجيّ بالتّوابع الرّياضيّة التّالية:
تكرار loop{

مع تحديث قيم θj تزامنيًّا بحسب j=0,1 }
تعبّر ألفا alpha عن معدّل التّعلّم، حيث يتمّ تحديد حجم خطوات الانحدار التّدريجيّ وهو يتّجه إلى الحدّ الأدنى المحليّ local minimum؛ ونقصد بالخطوة هنا تحديث قيم العوامل.
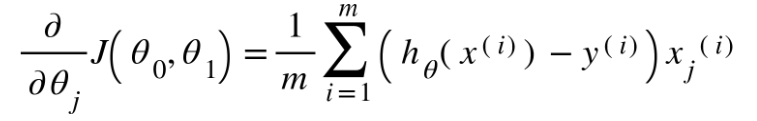
نلاحظ من التّوابع الرّياضيّة أنّها تحوي اشتقاقًا جزئيًّا، وذلك لأنّنا نبحث عن ميل العلاقة الخطّيّة المناسب والميل هو المشتقّ.
لكي تصل خوارزميّة الانحدار التّدريجيّ إلى الحدّ الأدنى المحليّ، يجب علينا ضبط معدّل التّعلّم على قيمة مناسبة وهي ليست منخفضة جدًّا ولا عالية جدًّا، لأنّه إذا كانت الخطوات التي تتّخذها كبيرة جدًّا فقد تصل الى الحد الأدنى لكنه لا يكون محليًّا لأنّها ترتدّ ذهابًا وإيابًا (انظر الصّورة اليسرى أدناه). وإذا كانت صغيرة جدًّا فإنّ الانحدار التّدريجيّ سيصل في النّهاية إلى الحدّ الأدنى المحليّ، ولكن قد يستغرق ذلك بعض الوقت لكنّ نتائجه ستكون دقيقة (انظر الصّورة الصّحيحة على اليمين).
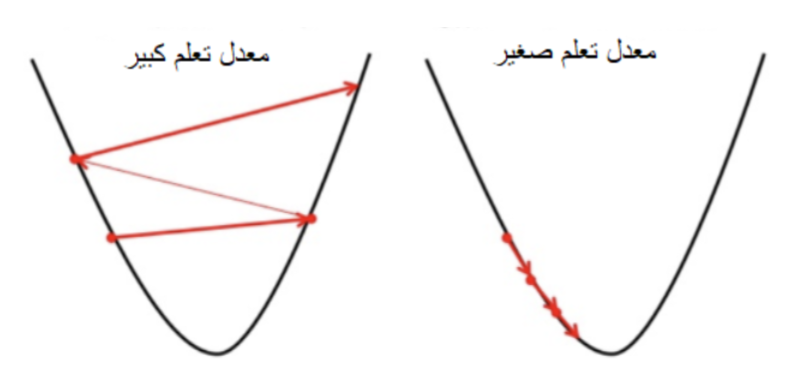
يمكننا تلخيص ما سبق بكلمات معدودة كما يلي:
علينا تصغير قيمة التّكلفة بواسطة الانحدار التّدريجيّ، وذلك بهدف الوصول إلى توقّع خطّيّ مثاليّ.
التّطبيق العمليّ:
الخطوة الأولى لأيّ مسألة في تعلّم الآلة هي الحصول على البيانات.
لا يوجد “تعلّم” آلة إذا لم يكن هناك شيء “للتعلّم” منه؛ لذا في هذا المقال سنستخدم مجموعة بيانات بسيطة جدًّا وهي مجموعة بيانات بغرض توقّع راتب موظّف بناءً على سنوات خبرته. يمكن تحميل مجموعة البيانات من هنا (موقع kaggle ).
سنبدأ باستدعاء المكتبات التي نحتاجها :
- مكتبة بايثون العدديّة numpy هي الحزمة الأساسيّة للعمل مع المصفوفات في لغة البرمجة بايثون.
- مكتبة تحليل البيانات في بايثون pandas وهي مختصّة بمعالجة البيانات وتحليلها وتقدّم ما يسمّى ب إطار البيانات (Data Frame)، والذي يسهّل من استيراد البيانات والتّعامل معها بسهولة.
- مكتبة الرّسم الرّياضيّ في بايثون matplotlib مكتبة مشهورة لرسم الرّسوم البيانيّة في بايثون.
- تقدّم مكتبة النّسخ copy مجموعة من عمليّات النّسخ السّطحيّة والعميقة.
- مكتبة الرّياضيّات math وهي مختصّة بجميع العمليّات والدّوال الرّياضيّة.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import copy
import math
%matplotlib inline
data = pd.read_csv('/content/Salary_Data.csv')
x_train = data.iloc[:,0] # قراءة العمود الأول
y_train = data.iloc[:,1] # قراءة العنود الثاني
print(len(y_train)) # عدد عينات التدريب
data.head() #إظهار أول خمسة أسطر من البيانات
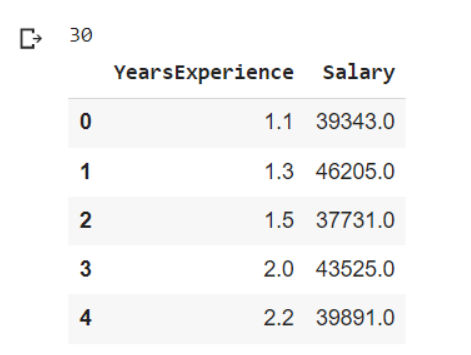
- تمثّل x_train بيانات التّدريب التي تعبّر عن عدد سنوات الخبرة للموظّف.
- تمثّل y_train بيانات التّدريب المعبّرة عن مقدار راتب الموظّف.
- نلاحظ أنّ عدد عيّنات التّدريب 30 موّظف وهو عدد قليل(لأنّ المثال توضيحيّ بسيط).
- التّابع head يظهر لنا أوّل خمس عيّنات من البيانات.
#رسم مخطط انتشار للبيانات
plt.scatter(x_train, y_train, marker='x', c='r')
# تحدبد العنوان
plt.title("years of experience vs salary")
# تحديد عنوان للمحور العمودي
plt.ylabel('salary')
# تحديد عنوان للمحور الأفقي
plt.xlabel('years of experience')
plt.show()

يظهر لنا الشّكل (5) مخطّط انتشار وهو عبارة عن مخطّط ارتباط يُستخدم للبحث في العلاقة بين متغيّرين، بحيث يكون أحد المتغيّرين مستقلًّا والآخر تابعًا يعتمد على المتغيّر الثّاني.
الخطوة التّالية هي تحويل تابع التّكلفة إلى شيفرة برمجيّة:
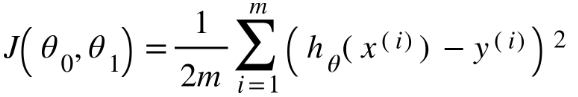
def cost_func(x, y, theta_1, theta_0):
# عدد عينات التدريب
m = x.shape[0]
#متغير يعبر عن قيمة التكلفة النهائية(يستخدم لاحقاً)
final_cost = 0
# متغير لمتابعة قيمة مجموع التكلفة لكل عينة
cost_sum = 0
# حلقة دورانية على كل العينات
for i in range(m):
# حساب القيمة المتوقعة لكل عينة
h = theta_1 * x[i] + theta_0
# حساب التكلفة لكل عينة
cost = (h - y[i]) ** 2
# إضافة التكلفة المحسوبة إلى مجموع العينات السابقة
cost_sum = cost_sum + cost
# حساب قيمة التكلفة النهائية
final_cost = (1 / (2 * m)) * cost_sum
return final_cost
قد استخدمنا حلقة دورانيّة لكي تمرّ الدّالة على كلّ عيّنات التّدريب في التّابع cost_func.
- يعبّر h عن القيمة المتوقّعة من خلال خوارزميّة التّوقّع الخطّيّ .
- يعبّر cost عن الفرق بين القيمة المتوقّعة والقيمة الفعليّة لكلّ عيّنة.
- يعبّر cost_sum عن مجموع الفروق بين القيم المتوقّعة والقيم الفعليّة.
- يعبّر final_cost عن النّتيجة النّهائيّة لتابع التّكلفة؛ وهي الخطأ بين القيمة المتوقّعة والقيمة الفعليّة .
تحويل تابع الانحدار التّدريجيّ إلى شيفرة برمجيّة :
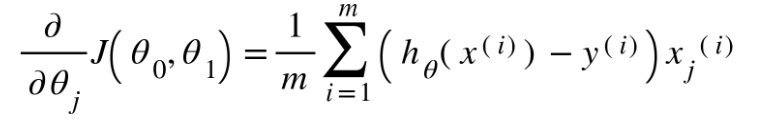
def gradient(x, y, theta_1, theta_0):
# عدد عينات التدريب
m = x.shape[0]
# (لحساب الانحدار التدريجي النهائي (متغيرات نستخدمها لاحقاً
j_theta_1 = 0
j_theta_0 = 0
# حلقة دورانية على عينات التدريب
for i in range(m):
#حساب القيمة المتوقعة لكل عينة
h = theta_1 * x[i] + theta_0
# حساب الانحدار التدريجي لكل عينة وفق العامل الأول
j_theta_1_i = (h - y[i]) * x[i]
# حساب الانحدار التدريجي لكل عينة وفق العامل الثاني
j_theta_0_i = h - y[i]
# تحديث قيمة الانحدار التدريجي
j_theta_0 += j_theta_0_i
j_theta_1 += j_theta_1_i
# تقسيم الانحدار التدريجي على عدد عينات التدريب
j_theta_1 = j_theta_1 / m
j_theta_0 = j_theta_0 / m
return j_theta_1, j_theta_0
قد استخدمنا حلقة دورانيّة لكي تمرّ الدّالة على كلّ عيّنات التّدريب في التّابع gradient.
- يعبّر j_theta_1_i عن الانحدار التّدريجيّ للعامل θ1 لكلّ عيّنة.
- يعبّر j_theta_0_i عن الانحدار التّدريجيّ للعامل θ0 لكلّ عيّنة.
- يعبّر j_theta_1 عن الانحدار التّدريجيّ النّهائيّ للعامل θ1 .
- يعبّر j_theta_0 عن الانحدار التّدريجيّ النّهائيّ للعامل θ0 .
يمكننا إيجاد العوامل المثاليّة من خلال حزمة الانحدار التّدريجيّ batch gradient descent والتي تعني استخدام كلّ عيّنات البيانات في كلّ دورة تدريب .
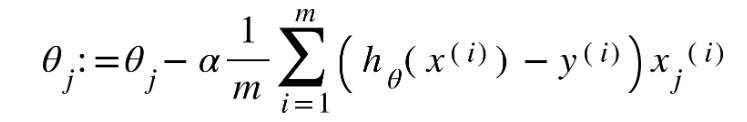
def gradient_descent(x, y, theta_1_in, theta_0_in, cost_function, gradient_function, alpha, num_iters):
# عدد عينات التدريب
m = len(x)
# مصفوفة تخزين بعد كل دورة تدريب
J_hist = []
theta_1_hist = []
theta_1 = copy.deepcopy(theta_1_in)
theta_0 = theta_0_in
for i in range(num_iters):
# حساب الانحدار التدريجي
j_theta_1, j_theta_0 = gradient_function(x, y, theta_1, theta_0 )
# تحديث العوامل
theta_1 = theta_1 - alpha * j_theta_1
theta_0 = theta_0 - alpha * j_theta_0
# تخزين قيمة التكلفة بعد كل دورة
return theta_1, theta_0
حساب قيم العوامل المثاليّة ومن الجدير بالذّكر أنّنا حدّدنا قيمة العامل alpha وعدد مرّات التّدريب.
# تحديد قيم ابتدائية للعوامل
initial_theta_1 = 0.
initial_theta_0 = 0.
iterations = 1500
alpha = 0.01
theta_1,theta_0 = gradient_descent(x_train ,y_train, initial_theta_1, initial_theta_0,
cost_func, gradient, alpha, iterations)
print("theta_1,theta_0 found by gradient descent:", theta_1, theta_0)

حساب القيمة المتوقّعة لكلّ عيّنات البيانات باستخدام حلقة دورانيّة
m = x_train.shape[0]
predicted = np.zeros(m)
for i in range(m):
predicted[i] = theta_1 * x_train[i] + theta_0
رسم الخطّ المعبّر عن الانحدار الخطّيّ وهو النّتيجة النّهائيّة المعبّرة عن العلاقة الخطّيّة بين راتب الموظّف وعدد سنوات خبرته.
#رسم خط الانحدار الخطي ضمن مخطط انتشار للبيانات
plt.plot(x_train , predicted,c="b")
plt.scatter(x_train, y_train, marker='x', c='r')
# تحدبد العنوان
plt.title("years of experience vs salary")
# تحديد عنوان للمحور العمودي
plt.ylabel('salary')
# تحديد عنوان للمحور الأفقي
plt.xlabel('years of experience')
plt.show()
للاطّلاع على الكود كاملًا من هنا
الخاتمة:
بدأنا في هذا المقال أوّل خطوة في مجال تعلّم الآلة وهي فهم أساسيّات خوارزميّة التّوقّع الخطّيّ Linear Regression، وضّحنا مفاهيم مهمّة كتابع التّكلفة cost function و الانحدار التّدريجيّ gradient descent وطبّقنا على ذلك مثالًا عمليًّا بسيطًا.



تعليق واحد
ممتاز . كيفية اعداد الداتا ست تجهيزها