التدقيق العلمي: د. م. حسن قزّاز، م. محمّد سرميني
التّدقيق اللغوي: هبة الله فلّاحة
المَحتويَات
- المقدمة:
- ما المقصود بكشف الحالات الشّاذّة؟Anomaly detection
- تطبيقات كشف الحالات الشّاذّة في الواقع:
- تصنيف الحالات الشّاذّة :
- الطرق المعتمدة على تعلّم الآلة من أجل الكشف عن الحالات الشاذة:
- 1-كشف الحالات الشاذّة اعتمادًا على العنقدة Clustering-Based Anomaly Detection
- 2- كشف الحالات الشاذّة اعتمادًا على الكثافة Density-based anomaly detection
- 3- كشف الحالات الشّاذّة اعتمادًا على خوارزميّة آلة المتّجه الدّاعم Support Vector Machine-Based Anomaly Detection
- 4- كشف الحالات الشّاذّة اعتمادًا على التّعلّم العميق الخاضع للإشرافSupervised Deep Anomaly Detection
- 5- كشف الحالات الشّاذّة اعتمادًا على التّعلّم العميق شبه الخاضع للإشراف Semi-supervised deep anomaly detection
- 6- الشبكة العصبونيّة ذات الصّنف الواحد (One-Class Neural Networks (OC-NN
- التّطبيق العمليّ :
- الخاتمة:
- المراجع:
المقدمة:
ماذا لو أنّ طائرة من بين مئات الطّائرات معرّضة لخطر الأعطال والسّقوط المفاجئ، هل نستطيع اكتشافها قبل حدوث الكارثة؟! وهل بإمكاننا أن نكتشف حالات الاختراق للتّحويلات البنكيّة قبل فقدان الأموال؟!وهل سيكون بوسعنا كشف حالات الاحتيال أو الأخطاء في مبيعات الشّركات التّجاريّة ؟!
لحسن الحظ أنّنا نستطيع منع كلّ تلك المشاكل من الحدوث باستخدام كشف الحالات الشاذّة Anomaly Detection ولكن ما هي ؟ وكيف تعمل ؟ وهل هي سهلة التّطبيق العمليّ ؟ هيا بنا لنتعرّف على هذه التّقنيّة المذهلة في هذا المقال.
ما المقصود بكشف الحالات الشّاذّة؟Anomaly detection
كشف الحالات الشّاذّة هي تقنيّة تستخدم لتحديد الأنماط غير الاعتياديّة التي لا تتوافق مع السّلوك المتوقّع للبيانات، وتعتبر عمليّة مدروسة لتحديد ما هو طبيعيّ وما هو غير طبيعيّ من العيّنات.
وهي غالبًا تطبّق على البيانات غير المعنونة Unlabeled وهو ما يعرف بكشف الحالات الشّاذّة غير الخاضع للإشراف unsupervised anomaly detection.
ويمكن الإشارة إلى الحالات الشّاذّة على أنّها قيم متطرّفة outliers، ضجيج، استثناءات أو انحرافات؛ أي أنّها حالات نادرة وتختلف ميّزاتها عن البيانات الطّبيعيّة.
سنطرح مثالًا بسيطًا للإيضاح : لنفترض أنّ لدينا مجموعة من طلّاب المدرسة، كيف سيكون أداؤهم في امتحان الرّياضيات مثلًا، ستكون نتيجة النّسبة الأكبر منهم متوزّعة ما بين 40% و 80% وهذا التّوزّع طبيعي، أمّا إذا وجد طالب نتيجته عالية جدًّا 99% أو طالب نتيجته منخفضة جدًّا 5% سنعتبر نتيجة هذَين الطالبين وما يشبهها حالات شاذّة (قيم متطرّفة).
وبصيغة أخرى، كشف الحالات الشاذة هو عبارة عن مهمة أو عملية لرسم حدود المنطقة الخاصة بالبيانات الطبيعية من أجل تسهيل عملية تمييز الحالات الشاذة أو المتطرفة.
حسناً، السّؤال الذي يراودنا الآن هو كيف نحدّد أنّ عيّنة ما هي حالة شاذّة أم لا ؟
في الحالات البسيطة، يستطيع الرّسم البيانيّ تزويدنا بمعلومات قيّمة كما هو موضّح بالشّكل (1).
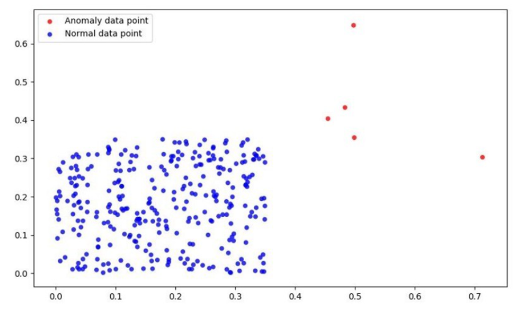
نلاحظ من الشّكل (1) إمكانيّة التّمييز بسهولة بين البيانات الطّبيعيّة الاعتياديّة (ذات اللّون الأزرق) التي تشكّل كتلة مترابطة ومتقاربة، وبين الحالات الشاذّة (ذات اللّون الأحمر) المبعثرة والبعيدة جدًّا.
من الجدير بالذكر أن القيم المتطرفة ليست بالضرورة سيئة دائماً، بل هناك حالات تكون فيها مفيدة ومثيرة للاهتمام والبحث.
ومثال ذلك : لنفترض أن لدينا تجربة علمية على مجموعة من الفئران، ونتج عن هذه التجربة موت جميع الفئران إلا فأراً واحداً (باعتبار أنّ الفئران هنا هم مجموعة البيانات المدروسة) .. أليس من المهم أن نبحث عن سبب نجاته ؟! مع أنّه يعتبر حالة شّاذّة، مما قد يقودنا لاكتشاف علمي جديد ..
تطبيقات كشف الحالات الشّاذّة في الواقع:
يمكن الاستفادة من هذه التّقنيّة في مجالات متنوّعة مثل:
- كشف التّسلّل وهو كشف حالات اختراق الشّبكة الحاسوبيّة .
- نظام مراقبة الصّحة في المستشفيات.
- كشف الاحتيال في تحويلات البطاقات البنكيّة.
- كشف الأخطاء في بيئات التّشغيل.
- كشف الأخبار الكاذبة والخاطئة في الشّبكة العنكبوتيّة.
- كشف الأعطال الصّناعيّة ( مثل أعطال الطّائرات ).
- الأمن والمراقبة.
تصنيف الحالات الشّاذّة :
1- حالات شاذّة نقطيّة Point Anomalies
تعتبر الحالة شاذّة إذا كانت بعيدة جدًّا عن مجموعة البيانات الطبيعية، ومثال ذلك كشف حالات الاحتيال في تحويلات البطاقات البنكيّة اعتمادًا على مقدار التّحويل أو السّحب.
2- حالات شاذّة سياقيّة Contextual Anomalies
يعتمد تحديد الحالات الشاذّة بناء على مجموعة من المعلومات تدل على تلك الحالات (contextual information)، وهذا الصّنف شائع في البيانات الزّمنيّة فمثلًا يصرف النّاس نقودًا أكثر في أيّام العطل مقارنة مع باقي الأيّام.
3- حالات شاذّة جماعيّة Collective Anomalies
تعتبر تشكيلة من البيانات المترابطة حالات شاذّة مقارنة ببقيّة البيانات الطبيعيّة (ليس كقيم فرديّة) ومثال ذلك، محاولة أحد الأشخاص إدخال تشكيلة من البيانات إلى مضيف محليّ بشكل غير متوقّع(هجوم إلكترونيّ محتمل).
الطرق المعتمدة على تعلّم الآلة من أجل الكشف عن الحالات الشاذة:
1-كشف الحالات الشاذّة اعتمادًا على العنقدة Clustering-Based Anomaly Detection
يدلّ تقارب أو تشابه مجموعة من العيّنات ضمن البيانات، على أنّها تنتمي إلى نفس العنقود وذلك قياسًا على بُعدها عن مركزه.
يمكن استخدام خوارزميّة التّجميع بالمتوسّطات The k-means algorithm التي تقوم بتقسيم مجموعة البيانات إلى رقم محدّد من العناقيد، وبهذا يمكن اعتبار النّقاط التي تقع خارج هذه العناقيد على أنّها حالات شاذّة.
2- كشف الحالات الشاذّة اعتمادًا على الكثافة Density-based anomaly detection
من الواضح أنّ البيانات الطبيعيّة تتواجد حول منطقة كثيفة وأنّ الحالات الشّاذّة تبتعد جدًّا عنها، ولقياس أقرب جوار لعيّنةٍ ما يمكنك استخدام المسافة الإقليدية أو مقياس مشابه حسب البيانات المدروسة.
تعتمد هذه الطّريقة على خوارزميّة الجوار الأقرب The KNN algorithm
3- كشف الحالات الشّاذّة اعتمادًا على خوارزميّة آلة المتّجه الدّاعم Support Vector Machine-Based Anomaly Detection
تعتبر هذه الخوارزميّة من الخوارزميات الفعّالة في هذا المجال، وقد تمّ تصميم خوارزميّة آلة المتّجه الدّاعم ذات الصّنف الواحد One-Class SVMs للحالات التي يتمّ فيها تحديد صنف واحد، والمشكلة تحديد أيّ عيّنة تقع خارج هذا الصّنف.
وهذا يُعرف ب novelty detection وهو يشير إلى التّحديد التّلقائيّ للظّواهر غير الطّبيعيّة، مثل القيم المتطرّفة المضمّنة في مجموعة كبيرة من البيانات الطّبيعيّة.
4- كشف الحالات الشّاذّة اعتمادًا على التّعلّم العميق الخاضع للإشرافSupervised Deep Anomaly Detection
بهذه الحالة يتمّ تدريب شبكة من أجل بناء مصنف يقوم بإسناد البيانات الطبيعية والشاذة إلى صنفين أو أكثر.
هذه الطّريقة تساعد في تحديد الماركات التّجاريّة النّادرة، أو اكتشاف اسم عقار محظور، أو حتّى الخدمات الصّحيّة الاحتياليّة .
5- كشف الحالات الشّاذّة اعتمادًا على التّعلّم العميق شبه الخاضع للإشراف Semi-supervised deep anomaly detection
وهي طريقة مستخدمة بشكل أوسع من الطّريقة السّابقة، لأنّ عناوين (Labels) البيانات الطّبيعيّة يسهل الحصول عليها مقارنة بالحالات الشّاذّة، حيث تستفيد هذه التّقنيّة من عناوين البيانات الطّبيعيّة لتحديد الحالات الشّاذّة.
6- الشبكة العصبونيّة ذات الصّنف الواحد (One-Class Neural Networks (OC-NN
تجمع هذه الطّريقة بين قدرة الشّبكات العميقة على تمثيل البيانات تدريجيًّا بشكل فعّال، مع قدرة الصّنف الواحد على رسم غلاف محكم أو حدود حول البيانات الطبيعيّة.
وبعد أن تعرّفنا على طرق كشف الحالات الشّاذّة، حان وقت التّطبيق العمليّ لهذه التّقنيّة.
التّطبيق العمليّ :
وسيكون هدف الدّراسة اكتشاف الحالات الشّاذّة في المبيعات والأرباح كلًّا على حدة (متغيّر واحد Univariate)، ومن ثمّ اكتشاف الحالات الشّاذّة في المبيعات والأرباح معًا (عدة متغيرات Multivariate).
لنبدأ أوّلًا باستدعاء المكتبات البرمجيّة :
import pandas as pd
import numpy as np
from numpy import percentile
import matplotlib.pyplot as plt
import seaborn as sns
import matplotlib
from sklearn.ensemble import IsolationForest
from sklearn.preprocessing import MinMaxScaler
سندرس مجموعة بيانات Super Store Sales Dataset يمكنك عزيزي القارئ أن تجد رابط تحميل مجموعة البيانات ورابط الشيفرة البرمجية في نهاية المقال.
df = pd.read_excel("/content/sample_data/Sample - Superstore.xls")
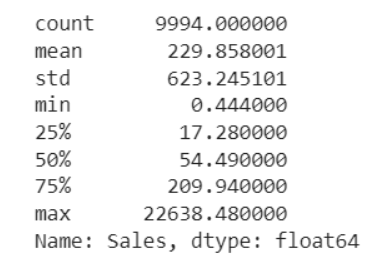
df['Sales'].describe()
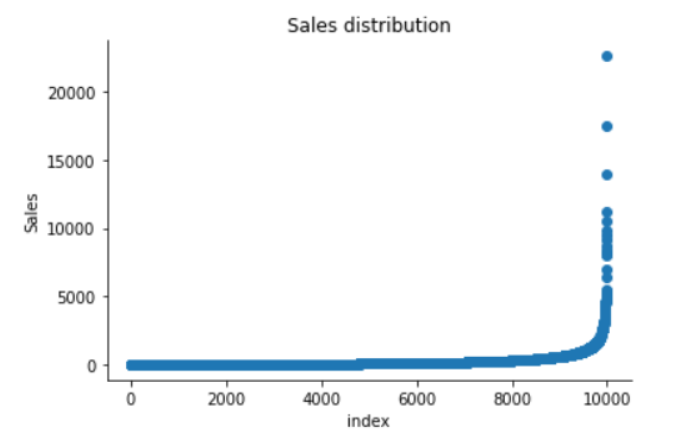
plt.scatter(range(df.shape[0]), np.sort(df['Sales'].values))
plt.xlabel('index')
plt.ylabel('Sales')
plt.title("Sales distribution")
sns.despine()
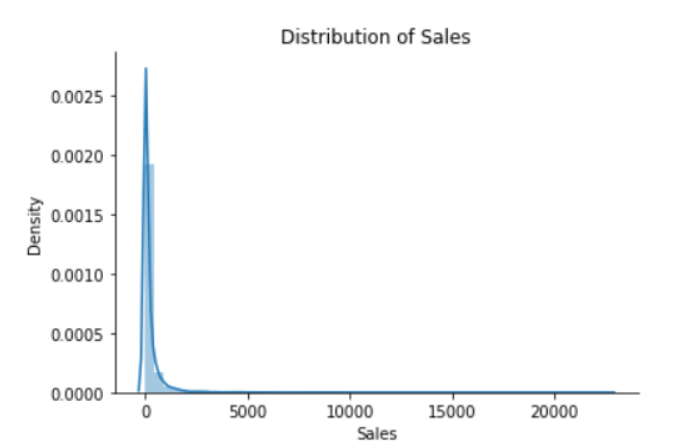
sns.distplot(df['Sales'])
plt.title("Distribution of Sales")
sns.despine()
print("Skewness: %f" % df['Sales'].skew())
print("Kurtosis: %f" % df['Sales'].kurt())
Skewness: 12.972752
Kurtosis: 305.311753
نلاحظ من الشكل (4) أنّ الكتلة الرئيسية من البيانات الخاصة بالمبيعات بعيدة جدًّا عن التّوزع الغوصي الطّبيعيّ، حيث أنّها تتركز على يسار الشكل، أما على يمين الشكل فتأخذ بيانات المبيعات شكل ذيل رفيع من القيم الموجبة الممتدة على كامل المحور.
df['Profit'].describe()
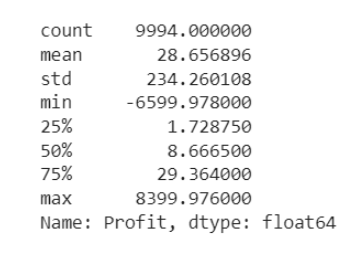
plt.scatter(range(df.shape[0]), np.sort(df['Profit'].values))
plt.xlabel('index')
plt.ylabel('Profit')
plt.title("Profit distribution")
sns.despine()
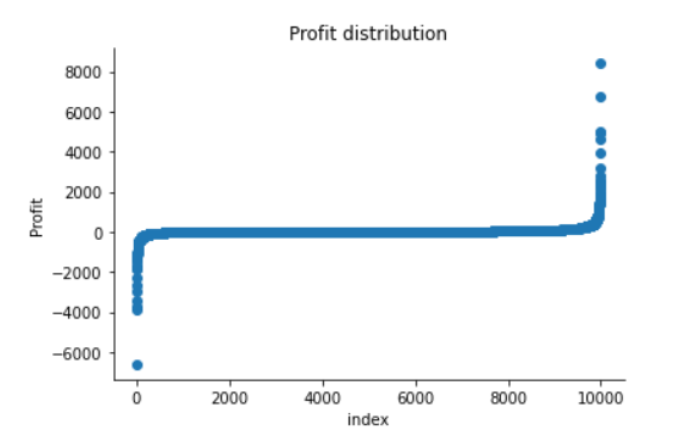
sns.distplot(df['Profit'])
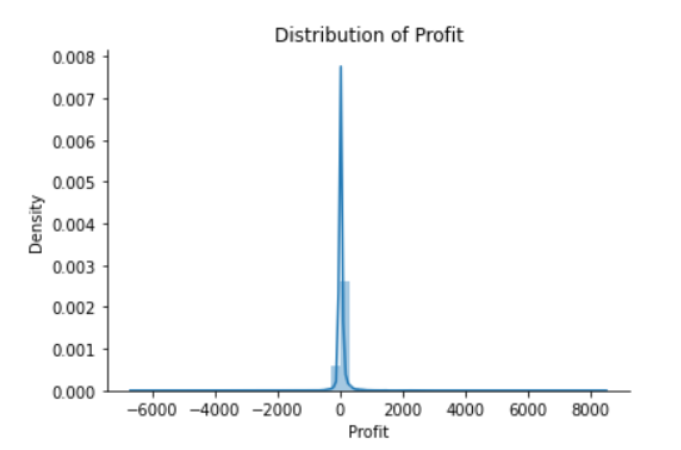
plt.title("Distribution of Profit")
sns.despine()
print("Skewness: %f" % df['Profit'].skew())
print("Kurtosis: %f" % df['Profit'].kurt())
Skewness: 7.561432
Kurtosis: 397.188515
من الشكل (7) نجد أن توزع العينات الخاصة بالأرباح له ذيل ذو قيم سالبة وذيل ذو قيم موجبة أطول من الذيل السابق، لذا فإن توزع العينات ينحرف نحو القيم الموجبة. ومن الواضح أنّ هناك منطقتان تنخفض فيهما احتمالية ظهور العينات الأولى على الجانب الأيمن من التوزع والثانية على الجانب الأيسر.
كشف الحالات الشّاذّة على متغيّر واحد وهو المبيعات:
سوف نستخدم خوارزمية غابة العزلة Isolation Forest من أجل إيجاد الحالات أو العينات الشاذة، حيث تعتمد هذه الخوارزمية على مبدأ ندرة واختلاف الحالات أو العينات الشاذة عن العينات الطبيعية، وهي قائمة على نموذج الشجرة.
يتم التقسيم الأولي لهذه الأشجار من خلال اختيار ميزة (feature) بشكل عشوائي واختيار القيمة التي سوف يتم تقسيم الأشجار عندها والتي تكون بين القيمة الصغرى والقيمة الكبرى للميزة المختارة.
فيما يلي سنقوم بتطبيق خوارزميّة Isolation Forest على ميزة المبيعات وفق الخطوات التّالية:
1- تدريب خوارزميّة Isolation Forest على بيانات المبيعات.
2- تخزين بيانات المبيعات ضمن مصفوفة عددية NumPy.
3- حساب مجموع نقاط الحالات الشّاذّة anomaly score لكلّ عيّنة.
4- تصنيف كلّ عيّنة يتمّ رصدها على أنّها قيمة متطرّفة أو ليست متطرّفة.
5- تحديد المناطق التي تنتمي إليها القيم الشاذة أو المتطرفة.
isolation_forest = IsolationForest(n_estimators=100)
isolation_forest.fit(df['Sales'].values.reshape(-1, 1))
xx = np.linspace(df['Sales'].min(), df['Sales'].max(), len(df)).reshape(-1,1)
anomaly_score = isolation_forest.decision_function(xx)
outlier = isolation_forest.predict(xx)
plt.figure(figsize=(10,4))
plt.plot(xx, anomaly_score, label='anomaly score')
plt.fill_between(xx.T[0], np.min(anomaly_score), np.max(anomaly_score),
where=outlier==-1, color='r',
alpha=.4, label='outlier region')
plt.legend()
plt.ylabel('anomaly score')
plt.xlabel('Sales')
plt.show();
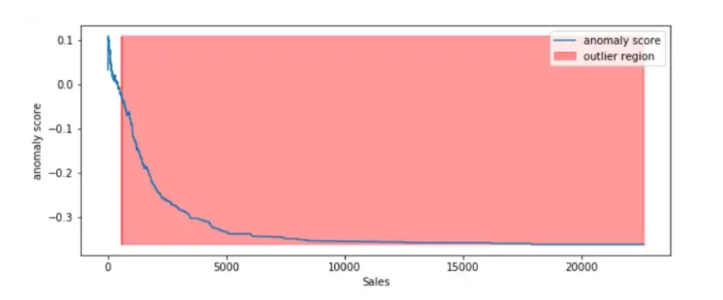
من خلال الشكل (8) والذي يوضح مجموع نقاط الحالات الشّاذّة anomaly score لكلّ العينات، نجد أن العينات الخاصة بالمبيعات التي تتجاوز 1000 تعتبر حالات شاذّة (قيم متطرّفة). للتّحقّق من عيّنة ما من الحالات الشّاذّة :
للتّحقّق من عيّنة ما من الحالات الشّاذّة :
df.iloc[10]
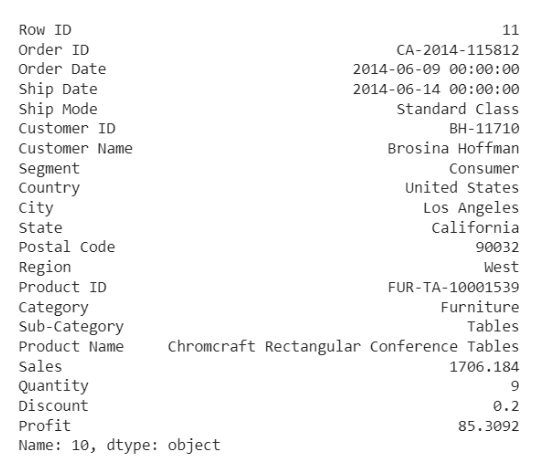
من الشكل (9) تبدو هذه العيّنة طبيعيّة لولا أنّها متجاوزة الحدّ الأعلى من المبيعات مقارنة مع باقي البيانات الطّبيعيّة.
فيما يلي سنقوم بتطبيق خوارزميّة Isolation Forest على ميزة الأرباح وفق الخطوات التّالية:
1- تدريب خوارزميّة Isolation Forest على بيانات الأرباح.
2- تخزين بيانات المبيعات ضمن مصفوفة Numpy.
3- حساب مجموع نقاط الحالات الشّاذّة anomaly score لكلّ عيّنة.
4- تصنيف كلّ عيّنة يتمّ رصدها على أنّها قيمة متطرّفة أو ليست متطرّفة.
5- تحديد المناطق التي تنتمي إليها القيم الشاذة أو المتطرفة.
isolation_forest = IsolationForest(n_estimators=100)
isolation_forest.fit(df['Profit'].values.reshape(-1, 1))
xx = np.linspace(df['Profit'].min(), df['Profit'].max(), len(df)).reshape(-1,1)
anomaly_score = isolation_forest.decision_function(xx)
outlier = isolation_forest.predict(xx)
plt.figure(figsize=(10,4))
plt.plot(xx, anomaly_score, label='anomaly score')
plt.fill_between(xx.T[0], np.min(anomaly_score), np.max(anomaly_score),
where=outlier==-1, color='r',
alpha=.4, label='outlier region')
plt.legend()
plt.ylabel('anomaly score')
plt.xlabel('Profit')
plt.show();
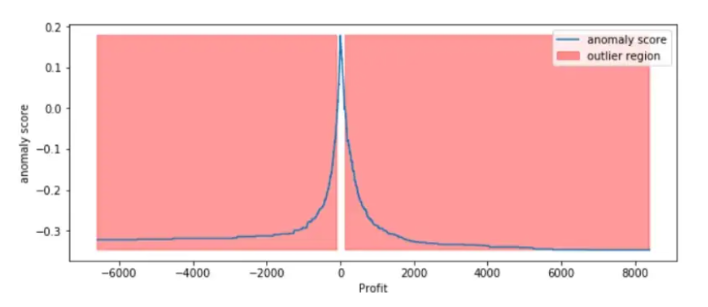
من خلال الشكل (10) والذي يوضح مجموع نقاط الحالات الشّاذّة anomaly score لكلّ العينات، نجد أن العينات الخاصة بالأرباح التي تقل عن -100وتتجاوز +100 تعتبر حالات شاذّة (قيم متطرّفة). للتّحقّق من عيّنة ما من الحالات الشّاذّة :
df.iloc[3]
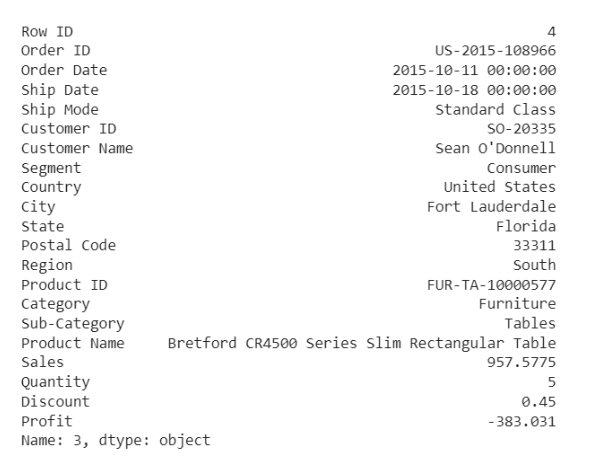
من البديهيّ أنّ أيّ ربح سالب يعتبر حالة شاذّة.
df.iloc[1]
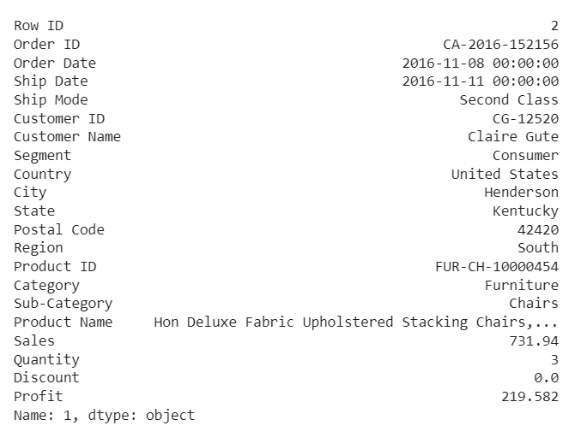
يبين الشكل (12) أنّ النموذج قام بتصنيف العينة على أنها حالة شاذة، وعندما نتحرى عن هذا الطلب، يمكن أن يكون مجرد منتج ذو هامش مرتفع نسبيًا.
نلاحظ أنّ التّطبيق على متغيّر واحد من الممكن أن يحدّد بعض الحالات على أنّها شاذّة وهي ليست بالضّرورة كذلك، وهذا ما يدفعنا إلى التّطبيق على عدّة متغيّرات multivariate وهذه الطّريقة أكثر تعقيدًا من النّاحية الحسابيّة، ولكنّها تعطينا نتائج أدقّ وهي الأكثر استخدامًا.
المبيعات والأرباح:
في عالم الأعمال نتوقّع أنّ هناك ترابط إيجابيّ بين المبيعات والأرباح، وإلّا فيمكن اعتبار العيّنة قيمة متطرّفة ويجب التحقّق منها،
وسوف نستخدم مكتبة PyOD وهي مكتبة بايثون تستخدم من أجل كشف الحالات الشاذة بالاعتماد على عدّة متغيرات.
sns.regplot(x="Sales", y="Profit", data=df)
sns.despine();
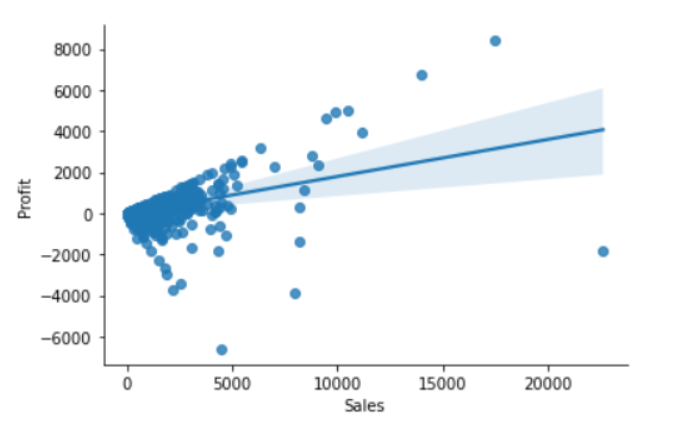
نلاحظ من الشّكل (13) أنّ القيم المتطرّفة هي إمّا المرتفعة جدًّا أو المنخفضة جدًّا .
عامل القيم المتطرّفة المحليّة المعتمد على العنقدة Cluster-based Local Outlier Factor (CBLOF)
يتمّ من خلاله حساب مجموع نقاط الحالة الشّاذّة Anomaly score، حيث يتمّ حساب المسافة بين كلّ عيّنة مع مركز العنقود التّابعة له، ومن ثمّ ضرب هذه المسافة المحسوبة بقيمة العيّنة، تتضمن مكتبة PyOD تطبيق عامل القيم المتطرّفة المحليّة المعتمد على العنقدة CBLOF.
الخطوات :
1- ضبط قيم scaling المبيعات والأرباح بين الصّفر والواحد .
2- إعطاء عامل القيم المتطرّفة 1% بشكل اعتباطيّ بناء على التّخمين والخبرة.
3- تدريب النموذج model على البيانات وتوقّع النّتائج.
4- تعيين قيمة العتبة والتي يتم من خلالها اتخاذ القرار باعتبار العيّنة حالة شاذّة (قيمة متطرّفة) أم لا .
5- استخدام تابع القرار decision function لحساب مجموع نقاط الحالات الشّاذّة anomaly score لكلّ عيّنة.
from pyod.models.cblof import CBLOF
outliers_fraction = 0.01
xx , yy = np.meshgrid(np.linspace(0, 1, 100), np.linspace(0, 1, 100))
clf = CBLOF(contamination=outliers_fraction,check_estimator=False, random_state=0)
clf.fit(X)
scores_pred = clf.decision_function(X) * -1
y_pred = clf.predict(X)
n_inliers = len(y_pred) - np.count_nonzero(y_pred)
n_outliers = np.count_nonzero(y_pred == 1)
plt.figure(figsize=(8, 8))
df1 = df
df1['outlier'] = y_pred.tolist()
# sales - inlier feature 1, profit - inlier feature 2
inliers_sales = np.array(df1['Sales'][df1['outlier'] == 0]).reshape(-1,1)
inliers_profit = np.array(df1['Profit'][df1['outlier'] == 0]).reshape(-1,1)
# sales - outlier feature 1, profit - outlier feature 2
outliers_sales = df1['Sales'][df1['outlier'] == 1].values.reshape(-1,1)
outliers_profit = df1['Profit'][df1['outlier'] == 1].values.reshape(-1,1)
print('OUTLIERS:',n_outliers,'INLIERS:',n_inliers)
threshold = percentile(scores_pred, 100 * outliers_fraction)
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()]) * -1
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, levels=np.linspace(Z.min(), threshold, 7),cmap=plt.cm.Blues_r)
a = plt.contour(xx, yy, Z, levels=[threshold],linewidths=2, colors='red')
plt.contourf(xx, yy, Z, levels=[threshold, Z.max()],colors='orange')
b = plt.scatter(inliers_sales, inliers_profit, c='white',s=20, edgecolor='k')
c = plt.scatter(outliers_sales, outliers_profit, c='black',s=20, edgecolor='k')
plt.axis('tight')
plt.legend([a.collections[0], b,c], ['learned decision function', 'inliers','outliers'],
prop=matplotlib.font_manager.FontProperties(size=20),loc='lower right')
plt.xlim((0, 1))
plt.ylim((0, 1))
plt.title('Cluster-based Local Outlier Factor (CBLOF)')
plt.show();
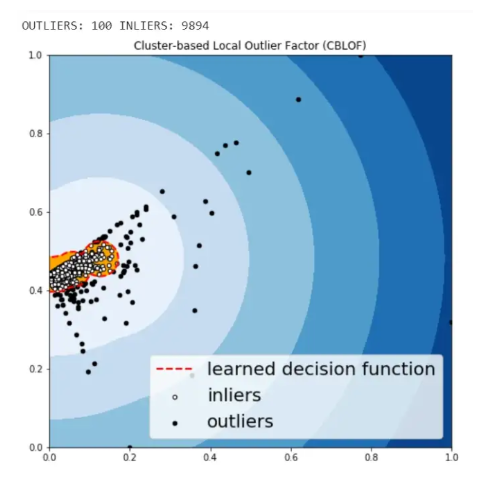
الشكل(14): كشف الحالات الشاذة باستخدام (CBLOF)
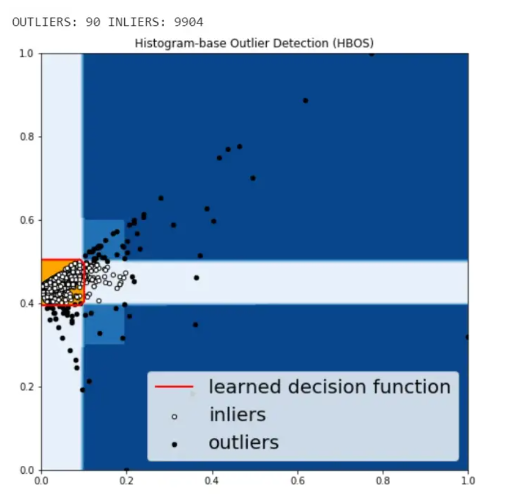
كشف الحالات الشّاذّة اعتمادًا على المخطّط البياني Histogram-based Outlier Detection (HBOS)
في هذه الطّريقة يتمّ التّعامل مع كلّ ميزة feature بشكل مستقل، ويتمّ كشف الحالات الشّاذّة من خلال رسم مخطّط هيستوغرام histogram لكلّ ميزة لوحدها، ومن ثمّ جمع المخطّطات معًا بالنّهاية.
عند استخدام مكتبة PyOD تكون الشيفرة البرمجية مشابهة ل CBLOF.
from pyod.models.hbos import HBOS
outliers_fraction = 0.01
xx , yy = np.meshgrid(np.linspace(0, 1, 100), np.linspace(0, 1, 100))
clf = HBOS(contamination=outliers_fraction)
clf.fit(X)
# predict raw anomaly score
scores_pred = clf.decision_function(X) * -1
# prediction of a datapoint category outlier or inlier
y_pred = clf.predict(X)
n_inliers = len(y_pred) - np.count_nonzero(y_pred)
n_outliers = np.count_nonzero(y_pred == 1)
plt.figure(figsize=(8, 8))
# copy of dataframe
df1 = df
df1['outlier'] = y_pred.tolist()
# sales - inlier feature 1, profit - inlier feature 2
inliers_sales = np.array(df1['Sales'][df1['outlier'] == 0]).reshape(-1,1)
inliers_profit = np.array(df1['Profit'][df1['outlier'] == 0]).reshape(-1,1)
# sales - outlier feature 1, profit - outlier feature 2
outliers_sales = df1['Sales'][df1['outlier'] == 1].values.reshape(-1,1)
outliers_profit = df1['Profit'][df1['outlier'] == 1].values.reshape(-1,1)
print('OUTLIERS:',n_outliers,'INLIERS:',n_inliers)
# threshold value to consider a datapoint inlier or outlier
threshold = percentile(scores_pred, 100 * outliers_fraction)
# decision function calculates the raw anomaly score for every point
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()]) * -1
Z = Z.reshape(xx.shape)
# fill blue map colormap from minimum anomaly score to threshold value
plt.contourf(xx, yy, Z, levels=np.linspace(Z.min(), threshold, 7),cmap=plt.cm.Blues_r)
# draw red contour line where anomaly score is equal to thresold
a = plt.contour(xx, yy, Z, levels=[threshold],linewidths=2, colors='red')
# fill orange contour lines where range of anomaly score is from threshold to maximum anomaly score
plt.contourf(xx, yy, Z, levels=[threshold, Z.max()],colors='orange')
b = plt.scatter(inliers_sales, inliers_profit, c='white',s=20, edgecolor='k')
c = plt.scatter(outliers_sales, outliers_profit, c='black',s=20, edgecolor='k')
plt.axis('tight')
plt.legend([a.collections[0], b,c], ['learned decision function', 'inliers','outliers'],
prop=matplotlib.font_manager.FontProperties(size=20),loc='lower right')
plt.xlim((0, 1))
plt.ylim((0, 1))
plt.title('Histogram-base Outlier Detection (HBOS)')
plt.show();
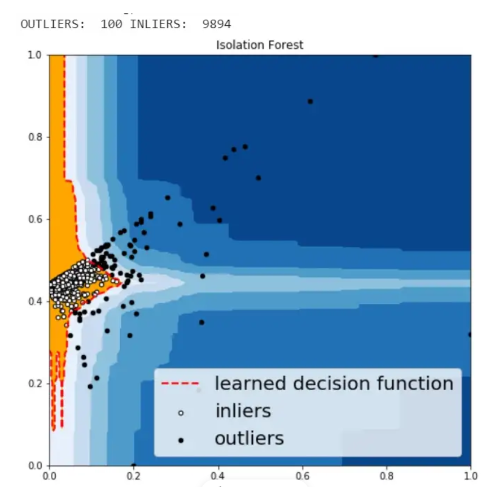
Isolation Forest خوارزمية غابة العزلة
وهي خوارزميّة شبيهة بخوارزميّة Random forest وهي مبنيّة بالاعتماد على أشجار القرار،
أمّا طريقة عملها فهي تختار ميزة ما feature بطريقة عشوائيّة، ومن ثمّ تختار قيمة من بين القيم الأعلى والقيم الأدنى لهذه الميزة.
كشف الحالات الشّاذّة باستخدام خوارزميّة الجوار الأقربK – Nearest Neighbors (KNN)
وهذه أبسط طريقة لكشف الحالات الشّاذّة، حيث يتمّ حساب مجموع نقاط الحالات الشّاذّة لعيّنة ما، من خلال قياس المسافة بينها وبين مركز أقرب جوار لها.
from pyod.models.knn import KNN
outliers_fraction = 0.01
xx , yy = np.meshgrid(np.linspace(0, 1, 100), np.linspace(0, 1, 100))
clf = KNN(contamination=outliers_fraction)
clf.fit(X)
# predict raw anomaly score
scores_pred = clf.decision_function(X) * -1
# prediction of a datapoint category outlier or inlier
y_pred = clf.predict(X)
n_inliers = len(y_pred) - np.count_nonzero(y_pred)
n_outliers = np.count_nonzero(y_pred == 1)
plt.figure(figsize=(8, 8))
# copy of dataframe
df1 = df
df1['outlier'] = y_pred.tolist()
# sales - inlier feature 1, profit - inlier feature 2
inliers_sales = np.array(df1['Sales'][df1['outlier'] == 0]).reshape(-1,1)
inliers_profit = np.array(df1['Profit'][df1['outlier'] == 0]).reshape(-1,1)
# sales - outlier feature 1, profit - outlier feature 2
outliers_sales = df1['Sales'][df1['outlier'] == 1].values.reshape(-1,1)
outliers_profit = df1['Profit'][df1['outlier'] == 1].values.reshape(-1,1)
print('OUTLIERS: ',n_outliers,'INLIERS: ',n_inliers)
# threshold value to consider a datapoint inlier or outlier
threshold = percentile(scores_pred, 100 * outliers_fraction)
# decision function calculates the raw anomaly score for every point
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()]) * -1
Z = Z.reshape(xx.shape)
# fill blue map colormap from minimum anomaly score to threshold value
plt.contourf(xx, yy, Z, levels=np.linspace(Z.min(), threshold, 7),cmap=plt.cm.Blues_r)
# draw red contour line where anomaly score is equal to thresold
a = plt.contour(xx, yy, Z, levels=[threshold],linewidths=2, colors='red')
# fill orange contour lines where range of anomaly score is from threshold to maximum anomaly score
plt.contourf(xx, yy, Z, levels=[threshold, Z.max()],colors='orange')
b = plt.scatter(inliers_sales, inliers_profit, c='white',s=20, edgecolor='k')
c = plt.scatter(outliers_sales, outliers_profit, c='black',s=20, edgecolor='k')
plt.axis('tight')
plt.legend([a.collections[0], b,c], ['learned decision function', 'inliers','outliers'],
prop=matplotlib.font_manager.FontProperties(size=20),loc='lower right')
plt.xlim((0, 1))
plt.ylim((0, 1))
plt.title('K Nearest Neighbors (KNN)')
plt.show();
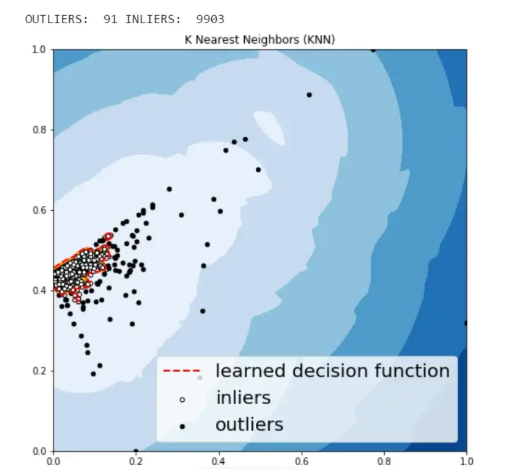
نلاحظ أنّ الحالات الشّاذة التي تمّ توقّعها من خلال الطّرق السّابقة لم تكن مختلفة كثيرًا فيما بينها.
للتّحقّق من بعض الحالات الشّاذّة:
df.iloc[1995]
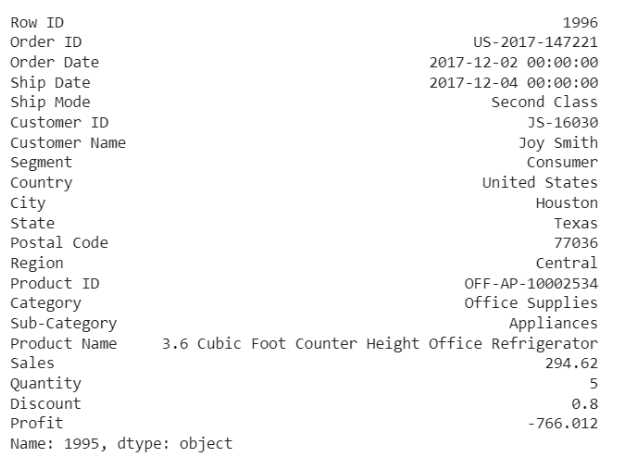
قام الزبون بشراء خمسة عناصر بسعر إجمالي 294.62 و ربح يساوي -766 بسبب تخفيضات قدرها 80%، وبالتالي نلاحظ أن هناك خسارة عند بيع تلك المنتجات أي الأرباح سالبة.
df.iloc[9649]
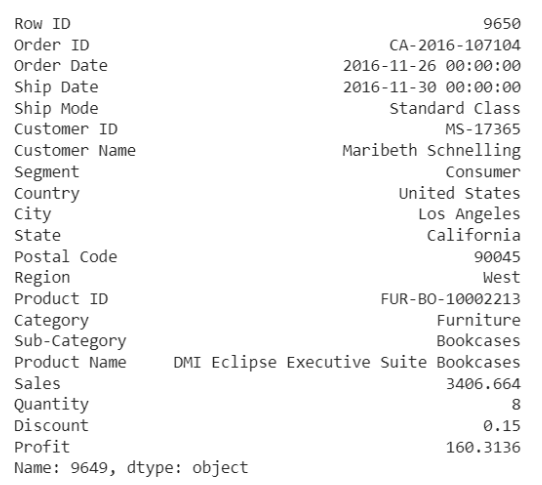
نلاحظ في هذه الحالة أنّ الربح منخفض جدًّا وقام النموذج بتصنيف هذه العملية على أنها حالة شاذة.
df.iloc[9270]
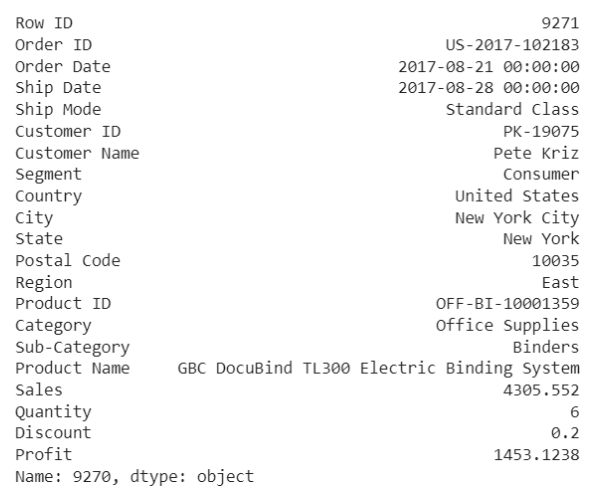
أمّا في هذه الحالة نجد أنّ الزّبون قد طلب 6 منتجات وحصل على تخفيض 20% ونجد أنّ الرّبح كبير، ومثل هذه الحالات الشّاذّة تكون مرغوبة في الشّركات التّجاريّة.
يمكنك عزيزي القارئ أن تجد الكود البرمجيّ كاملًا هنا وتحميل مجموعة البيانات المستخدمة من هنا.
الخاتمة:
تعرّفنا في هذا المقال على تقنيّة مفيدة جدًّا بالحياة العمليّة؛ وهي كشف الحالات الشّاذّة ضمن مجموعة البيانات والتي تسلك سلوكًا غير متوقّع، ورأينا تصنيفاتها وطرق تطبيقها، كما وضّحنا آليّة تنفيذها من خلال تطبيق عمليّ برمجيّ بلغة بايثون.