المحتويات:
- المقدّمة
- أنواع النقاط الشاذة
- الشذوذ العام
- الشذوذ الخارج عن السياق
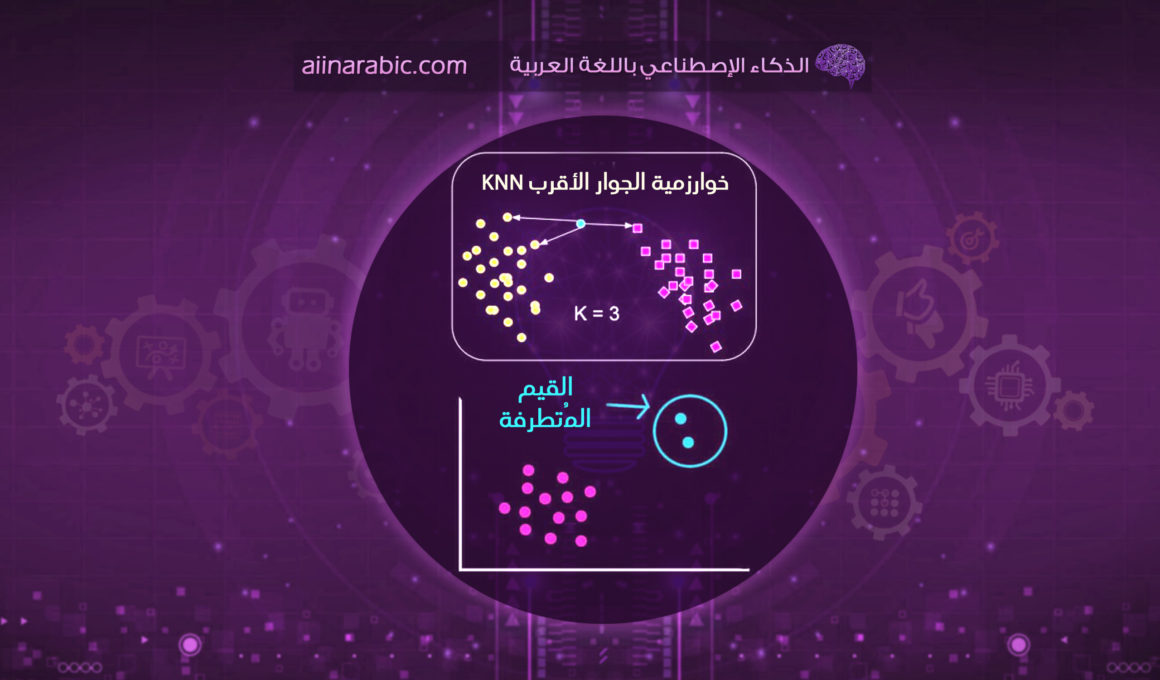
- خوارزمية الجيران الأقرب
- مثال نظري حول خوارزمية الجيران الأقرب
- الخاتمة
- المصادر
المقدمة Introduction
يُعتبر علمُ البيانات من أكثرِ المجالات شهرةً في السّنوات الأخيرة، حيث يختلف الباحثون وروّاد الذّكاء الاصطناعيّ حول تعريفٍ مناسب لهذا المصطلح، ولكنهم يتفقون دون أدنى شكٍّ على أنه علمٌ قائمٌ على المهارةِ الإحصائيّة والبرمجيّة، يُستخدم في تحليل بياناتٍ خام وتحويلها إلى معلوماتٍ مفيدة يُمكن فهمها وتحليلها واستخلاص نتائجَ مفيدةٍ منها، بحيث يدخلُ هذا المجال في حلّ العديد من المشاكل التي نواجهها في حياتنا اليوميّة، ومن أهمها اكتشافُ الشذوذ Anomaly Detection، ويقصد به تحديد العناصر النّادرة أو الأحداث أو الملاحظات التي تثيرُ الشكوكَ باختلافها بشكلٍ كبير عن غالبيّة البيانات. بحيث يوجدُ العديد من الخوارزميّات المستخدمة لاكتشافِ الشذوذ ومن أهمّها خوارزميّة الجارِ الأقرب KNN والتي تُعتبر من أهمّ خوارزميّات التعلّم الآليّ .
أنواعُ النقاطِ الشاذّة
1- الشذوذ العام Global Anomaly
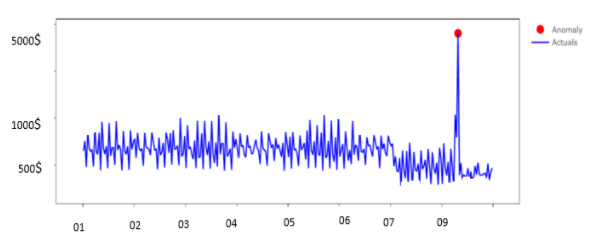
يُقصد بها حدوثُ حدثٍ مفاجئ في الظاهرةِ المدروسة مختلفة عن السياق الطبيعيّ لها، وتُسمى هذه الحالة بالنقاطِ الشاذّة العامة، ولتوضيحها بشكلٍ أبسط سوف نقوم بطرحِ مثالٍ عليها بفرضٍ لدينا عميلٌ بنكيّ اعتاد على إيداعِ ما لا يزيدُ عن 1000 دولارٍ شهرياً، وفجأةً قام بإيداعِ أكثر من 5000 دولارٍ خلال فترةٍ زمنيّة لا تتجاوزُ الأسبوعَين كما في الشكلِ 1 فهذه الحالة تندرجُ تحت صنفِ الشذوذِ العام لأنّ هذا الحدث لم يحصلْ سابقاً في تاريخِ العميل، لذلك يجبُ مساءلة هذا العميل لأنّ هذه الودائع الكبيرة من الممكنِ أن يكون قد حصل عليها بطرق غير مشروعة ربما غسيل أموال .
2. الشذوذ الخارج عن السياق Contextual Anomaly
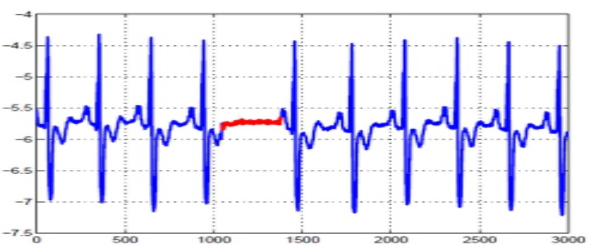
يُقصد بها حدوث حدث مفاجئ في الظاهرة المدروسة عن السياق الطبيعيّ لها لفترة زمنيّة محدودة وبعدها تعود الظاهرة المدروسة لوضعها الطبيعي،ّ , وأشهر مثال على هذه الحالة جهاز تخطيط القلب وذلك عندما يكون وضع القلب طبيعيّاً ويتوقف فجأةً وبعدها يعود لوضعه الطبيعيّ بعد تعرّضه لبعض الصدمات الكهربائيّة/ كما في الشكل 2 وتسمى هذه الحالة بالنقاط الشاذّة الخارجة عن السّياق .
خوارزميّة الجيران الأقرب K Nearest Neighbor
هي إحدى خوارزميّات التعلم الآليّ الخاضعة للإشراف المستخدمة في مجال التصنيف والانحدار، وتعتمد على تخزينِ جميع البيانات المتوفرة لدينا مع الخرج الموافق لها، ليتمّ فيما بعد تصنيف بياناتٍ جديدة بناءً على مقياس معين بالاعتماد على الخرج المقابل لنقاط الجيران الأقرب بحيث يعبر K عن عدد النقاط، ويتمّ تحديده بالتّجريب من خلال مقارنة خطأ التّدريب مع خطأ الاختبار، وباللحظة التي يُصبح بها الخطآن متقاربَين أي في حالة توازن عندها نكون قد وصلنا لقيمة K المثاليّة. وتعتبر هذه الخوارزميّة من أهمّ الخوارزميّات التي تُساعد علماء البيانات في اكتشاف النقاط الشاذّة.
ملاحظة : في المهمّات التي تتطلب منّا التصنيف بين صنفَين، من المفضّل أن تكون قيمة k فرديّة سنوضح السبب في الأسفل .
ولكن بدايةً دعونا نجيب على التساؤل التالي : ما هو المقصود بتصنيف بيانات جديدة بالاعتماد على الخرج المقابل لنقاط الجيران الأقرب؟
تَخيل أنك انتقلت لحيٍّ جديد ويوجد فيه مطعمين، وأنت لاتعلم سوى موقعهما وتريد أن تعرف ما هو المطعم الأفضل لكي تشتري منه؟ بكلّ بساطة تتصل بأقرب جيرانك وتأخذ رأيهم ثم تختار المطعم الأفضل بناءً على رأي الأكثريّة.
إنّ ماتمّ ذكره عزيزي القارئ ينطبق على خوارزميّة الجار الأقرب، فنلاحظ أنّ لهذه الخوارزميّة من اسمها نصيباً فهي تتصرّف مثل طريقتك ولكن بمعادلة رياضيّة لطيفة هي قانون اقليدس.
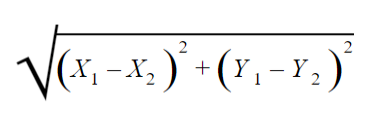
مثال نظريّ حول خوارزميّة الجيران الأقرب Example
ليكن لدينا قاعدة البيانات التالية التي تعبر عن المطرب المفضّل للأشخاص :
|
المطرب المفضل |
الجنس |
العمر |
الإسم |
|
تايلور سويفت |
M |
32 |
بيل |
|
تايلور سويفت |
M |
40 |
هينري |
|
رولينغ ستونز |
F |
16 |
ماري |
|
تايلور سويفت |
F |
14 |
تريفاني |
|
رولينغ ستونز |
M |
56 |
ميشيل |
|
تايلور سويفت |
M |
40 |
كارلوس |
|
رولينغ ستونز |
F |
20 |
سارا |
|
تايلور سويفت |
M |
15 |
ريبيرت |
|
رولينغ ستونز |
F |
56 |
سالي |
|
تايلور سويفت |
M |
15 |
جوني |
نلاحظ أنّ لدينا عدد مزايا الدّخل يساوي 3 والخرج لدينا صنفان والمطلوب :
التنبّؤ بمطرب ريم المفضّل بحيث عمرها 5 سنوات ؟
نطبق الخطوات التالية :
- نلاحظ أنّ ميزة الاسم لاتؤثر على الخرج، بالتالي سوف يتمّ تجاهل ميزة الاسم ونعتمد على ميّزتي العمر والجنس في اختيار المطرب المفضّل .
- نلاحظ أنّ قيم عمود الجنس يعبر عن محارف، وهذا لا يفيدنا في العمليّات الحسابيّة بالتالي سنستبدل نُعبر عن الذكر بالرقم 0 والأنثى بالرقم 1 بالتالي تصبح قاعدة البيانات السّابقة بالشكل التالي :
|
المطرب المفضل |
الجنس |
العمر |
الإسم |
|
تايلور سويفت |
0 |
32 |
بيل |
|
تايلور سويفت |
0 |
40 |
هينري |
|
رولينغ ستونز |
1 |
16 |
ماري |
|
تايلور سويفت |
1 |
14 |
تريفاني |
|
رولينغ ستونز |
0 |
56 |
ميشيل |
|
تايلور سويفت |
0 |
40 |
كارلوس |
|
رولينغ ستونز |
1 |
20 |
سارا |
|
تايلور سويفت |
0 |
15 |
ريبيرت |
|
رولينغ ستونز |
1 |
56 |
سالي |
|
تايلور سويفت |
0 |
15 |
جوني |
3. نُطبق معادلة إقليدس بين ريم وكلّ شخص في قاعدة البيانات .
اذاً نبدأ ببيل : الجنس ذكر أي 0 والعمر 32 فنجد
ونكرّر ذلك من أجل جميع الأشخاص في قاعدة البيانات، فنحصل على مايلي :
|
المطرب المفضل |
المسافة |
الجنس |
العمر |
الإسم |
|
تايلور سويفت |
27.02 |
0 |
32 |
بيل |
|
تايلور سويفت |
35.01 |
0 |
40 |
هينري |
|
رولينغ ستونز |
11.00 |
1 |
16 |
ماري |
|
تايلور سويفت |
9.00 |
1 |
14 |
تريفاني |
|
رولينغ ستونز |
50.01 |
0 |
56 |
ميشيل |
|
تايلور سويفت |
35.01 |
0 |
40 |
كارلوس |
|
رولينغ ستونز |
15.00 |
1 |
20 |
سارا |
|
تايلور سويفت |
10.00 |
0 |
15 |
ريبيرت |
|
رولينغ ستونز |
50.00 |
1 |
56 |
سالي |
|
تايلور سويفت |
10.05 |
0 |
15 |
جوني |
4. نرتب قاعدة البيانات السّابقة ترتيباً تصاعديّاً بالاعتماد على ميزة المسافة .
|
المطرب المفضل |
المسافة |
الجنس |
العمر |
الإسم |
|
تايلور سويفت |
9.00 |
1 |
14 |
تريفاني |
|
تايلور سويفت |
10.00 |
0 |
15 |
ريبيرت |
|
تايلور سويفت |
10.05 |
0 |
15 |
جوني |
|
رولينغ ستونز |
11.00 |
1 |
16 |
ماري |
|
رولينغ ستونز |
15.00 |
1 |
20 |
سارا |
|
تايلور سويفت |
27.02 |
0 |
32 |
بيل |
|
تايلور سويفت |
35.01 |
0 |
40 |
كارلوس |
|
تايلور سويفت |
35.01 |
0 |
40 |
هينري |
|
رولينغ ستونز |
50.00 |
1 |
56 |
سالي |
|
رولينغ ستونز |
50.01 |
0 |
56 |
ميشيل |
5. تحديد عدد نقاط الجيران الأقرب ولتكن K=3 هي القيمة المثاليّة، بالتالي نختار أوّل ثلاث قيم من الجدول السابق فنلاحظ أنّ:
- خصائص ريم تبعد عن خصائص تيفاني بمسافة 9 ومطربها المفضّل تايلور سويفت .
- خصائص ريم تبعد عن خصائص روبيرت بمسافة 10 ومطربها المفضّل تايلور سويفت .
- خصائص ريم تبعد عن خصائص جون بمسافة 10.05 ومطربها المفضّل رولينغ ستونز.
أي نتيجتان لصالح تايلور ونتيجة لصالح رولينغ، بالتالي حسب الأكثريّة والجيران الأقرب ل ريم نجد أنّ مطربها المفضّل هو تايلور .
ملاحظة : نلاحظ لو كانت قيمة k زوجيّة مثلاً 4 وكانت النتائج متوازنة أي نتيجتان لصالح كلّ مطرب، بالتالي سنقع في الالتباس في اختيار المطرب المفضّل لريم، و لتجنب هذا الالتباس يُفضّل أن تكون قيمة k فرديّة .
اكتشاف النقاط الشاذّة باستخدام خوارزميّة الجيران الأقرب :
يتمّ اكتشاف النقاط الشاذّة باستخدام طريقتين
1) اكتشاف النقاط الشاذّة من خلال عرض البيانات :
بفرض لدينا مجموعة من البيانات تعبر عن النّبيذ بلونيه الأحمر والأبيض، السؤال الأهمّ ماهو الفرق بين النّبيذ الأحمر والأبيض ؟ قد يظنّ البعض أنّ النّبيذ الأحمر مصنوع من العنب الأحمر والنّبيذ الأبيض مصنوع من العنب الأبيض ( الأخضر )، ولكنّ هذا الكلام غير دقيق فمن الممكن أن يُصنع النّبيذ الأبيض من العنب الأحمر .
الفرق الأساسيّ يكمن في طريقة تخمير العنب ليصبح نبيذاً سواء كان أبيضاً أم أحمراً .
لتصنيع نبيذ أحمر يتمّ تخمير عصير العنب مع قشره لفترة زمنيّة مطوّلة مع قشره، أما لتصنيع نبيذ أحمر يتمّ تخمير عصير العنب لفترة زمنيّة طويلة بدون قشره، فإنّ وجود قشور العنب في عمليّة التخمير لايؤثر فقط على لون النبيذ بل أيضاً يؤثر على تركيبته الكيميائيّة أي بمعنى آخر يمكن معرفة لونه من خلال طعمته .سنأتي للفكرة الأهمّ وهي استخدام خوارزميّة ال KNN في تحديد لون النبيذ بناءً على مكوّناته الكيميائيّة .
بفرض لدينا مجموعة بيانات تعبر عن لون النبيذ إذا كان أحمراً أم أبيضاً بناءً على كميّة الصّوديوم وثاني أوكسيد الكبريت:
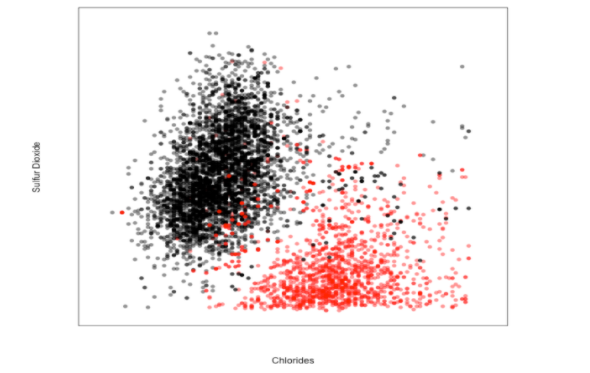
نحن نعلم أنّ نسبة الصّوديوم أي ملح الطعام تتواجد بشكل أكبر في القشر الخارجيّ للعنب، يتميز القشر الخارجيّ باحتوائه على مضادّات أكسدة طبيعيّة أي ثاني أوكسيد الكبريت التي تجعل الفاكهة طازجة، نلاحظ من الفقرة السابقة أنّ النبيذ الأحمر يحتوي على نسبة صوديوم عالية لهذا السبب نلاحظ مجموعة نقاط النبيذ الأحمر تتجمع في الجهة السفلى اليمينيّة من المخطط ، أمّا النبيذ الأبيض فكان يفتقد للقشر الخارجيّ للعنب بالتالي يحتاج إلى كمية كبيرة من ثاني أوكسيد الكبريت لهذا السبب نلاحظ مجموعة نقاط النبيذ الأسود ( أي الأبيض ) تتجمع في الجهة العليا اليساريّة من المخطّط .
من أجل تصنيف لون النبيذ يتمّ ذلك من خلال معرفة الألوان المجاورة للنقطة المدروسة، بحيث تكون نسبة الصوديوم وثاني أوكسيد الكربون في النقطة المدروسة متقاربة إلى حدٍّ ما مع نسب النقاط المجاورة، بالتالي إذا طبقنا هذه المنهجيّة من أجل جميع النقاط نحصل في النهاية على حدود القرار التي تفصل النبيذ الأحمر عن الأبيض .
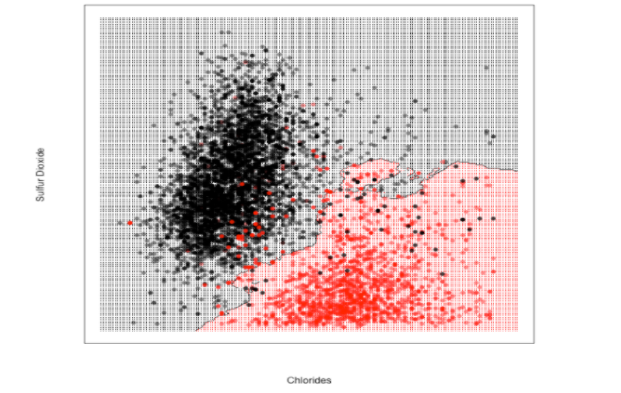
تمّ تجريب 3 قيم لعدد الجيران وهي 3 ,17 , 50 كما يلي :
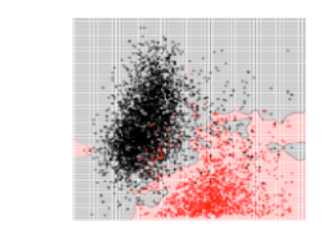
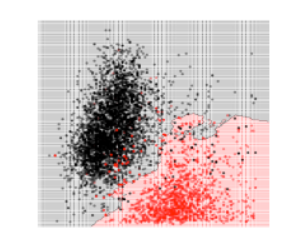
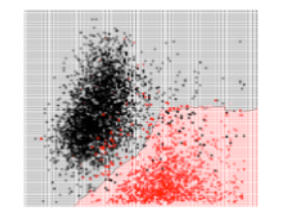
بالمقارنة بين الأشكال الثلاثة نجد أنّه عندما كانت قيمة K صغيرة أي 3 ظهرت معنا مشكلة الملاءمة القوية Overfitting وهذا أمر منطقيّ لأنّ كلّ نقطة يتمّ تصنيف الخرج لها بناءً على النقاط القريبة منها بشكل كبير، بالتالي لا وجود لمجال الخطأ وهذا يعني أنّ الموديل قد بصم مجموعة البيانات . ونلاحظ أنّه عندما كانت قيمة K كبيرة أي 50 ظهرت معنا مشكلة الملاءمة الضعيفة Underfitting بينما إذا كانت قيمة K متوسطة أي 17 نلاحظ أننا وصلنا لتوازن أي الموديل لايعاني من مشكلة الملاءمة القوية ولا من مشكلة الملاءمة الضعيفة لهذا السبب تمّ اعتماد قيمة K = 17 كقيمة مثاليّة في عمليّة اتخاذ حدود القرار .
بعد أن قُمنا بعرض وتدريب الخوارزميّة على مجموعة البيانات كما في الشكل 2 نلاحظ وجود بعض النقاط التي تنتمي للنبيذ الأبيض تمّ تصنيفها على أنها تنتمي للنبيذ الأحمر بالمقابل أيضاً نجد بعض النقاط التي تنتمي للنبيذ الأحمر تمّ تصنيفها على أنها تنتمي للنبيذ الأبيض، جميع هذه النقاط التي تحدثنا عنا تُعتبر نقاطاً شاذّة Anomaly ومن المفضّل التّخلص منها قبل القيام بعمليّة التدريب لأنّ وجودها بالتأكيد يزيد من زمن التدريب وايضاً يؤثّر على دقة الموديل .
2) اكتشاف النقاط الشاذّة من خلال إيجاد متوسط المسافات بين كلّ نقطة من نقاط البيانات مع النقاط الأخرى:
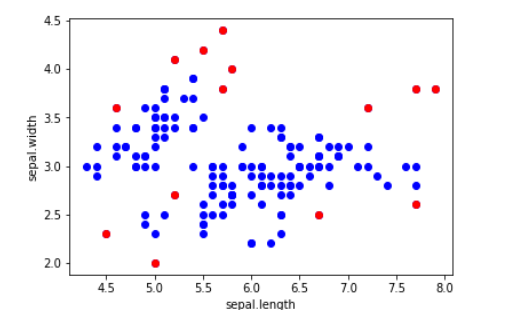
بفرض لدينا مجموعة البيانات الشهيرة التي تعبر عن انواع الزهور تحتوي على 150 عيّنة وكلّ عيّنة تنتمي إلى إحدى الأنواع الثلاثة سيتوسا , فيرسي كولور, فيرجينيا بحيث يتمّ تصنيف الزّهرة اعتماداً على ميّزة عرض وطول الورقة .
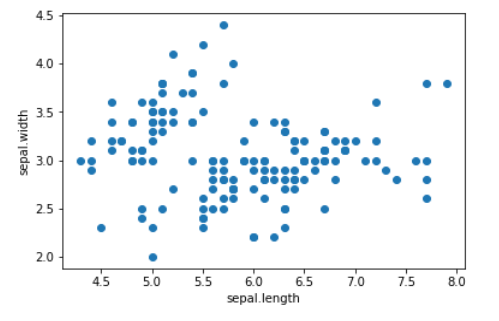
إذا قُمنا بتطبيق خوارزميّة الجار الأقرب على البيانات السابقة مع تحديد عدد الجيران وليكن 3، عندها نستطيع معرفة بُعد كلّ نقطة عن باقي النقاط الأخرى بالتالي يُصبح لدينا 150 شعاعاً وكلّ شعاع يحتوي على 150 قيمة، عندها نقوم بحساب المتوسط الحسابيّ لكلّ شعاع وبذلك نكون قد حصلنا على متوسط المسافة لكلّ نقطة عن النقاط الأخرى كالتالي:

نلاحظ أنّ أغلب مجال متوسط المسافات لكلّ نقطة مدروسة مع النقاط الثلاث المجاورة لها يتراوح ما بين 0.00 و 0.15 وعدد قليل من النقاط المدروسة متوسط المسافة لها أكبر من 0.15، بالتالي تُعتبر هذه النقاط نقاطاً شاذّة سوف نقوم بتحديدها من بين مجموعة البيانات ككلّ.
بعد أن عرفنا النقاط الشاذّة كان علينا التخلص منها لأنها تؤثر على أداء وتصنيف الموديل فنقوم بحذفها من مجموعة البيانات الأصليّة كالتالي :
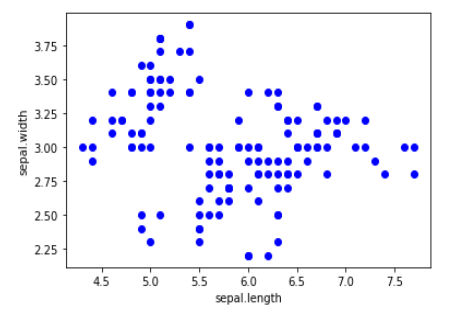
بعد أن قُمنا بحذف النقاط الشاذّة نقوم بعملييّة إيجاد متوسط المسافات للنقاط المتبقية
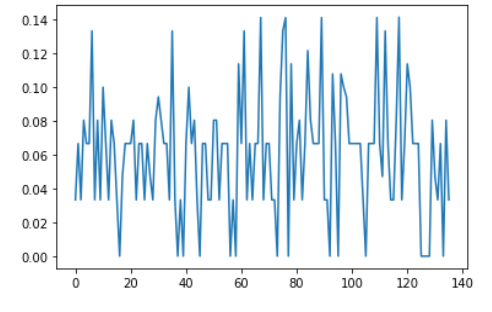
نلاحظ أنّ مجال متوسط المسافات لجميع النقاط يتراوح مابين القيمة 0.00 و 0.14 ، وبهذا نكون قد تخلصنا من النقاط الشاذّة بالاعتماد على خوارزميّة الجار الأقرب.
الخاتمة
تعرّفنا في هذا المقال على أهمّ المشاكل التي تواجه علماء البيانات، وهي اكتشاف الأحداث الشاذّة أو المتطرّفة في مجموعة البيانات، وتعرّفنا على أنواع الشذوذ وقُمنا بتوضيح الفرق بينهما من خلال مثال بسيط، وبعد ذلك قُمنا بالتعرّف على أشهر خوارزميّات التعلم الآليّ وهي خوارزميّة الجار الأقرب، وقمنا بتوضيح مبدأ عملها بمثال نظريّ والأهمّ من ذلك قمنا بتطبيقها في عمليّة اكتشاف الشذوذ الذي يعتبر جوهر مقالتنا.
المصادر
1.Machine learning what is anomaly detection
2.Types of anomaly detection