الانحدار Regression

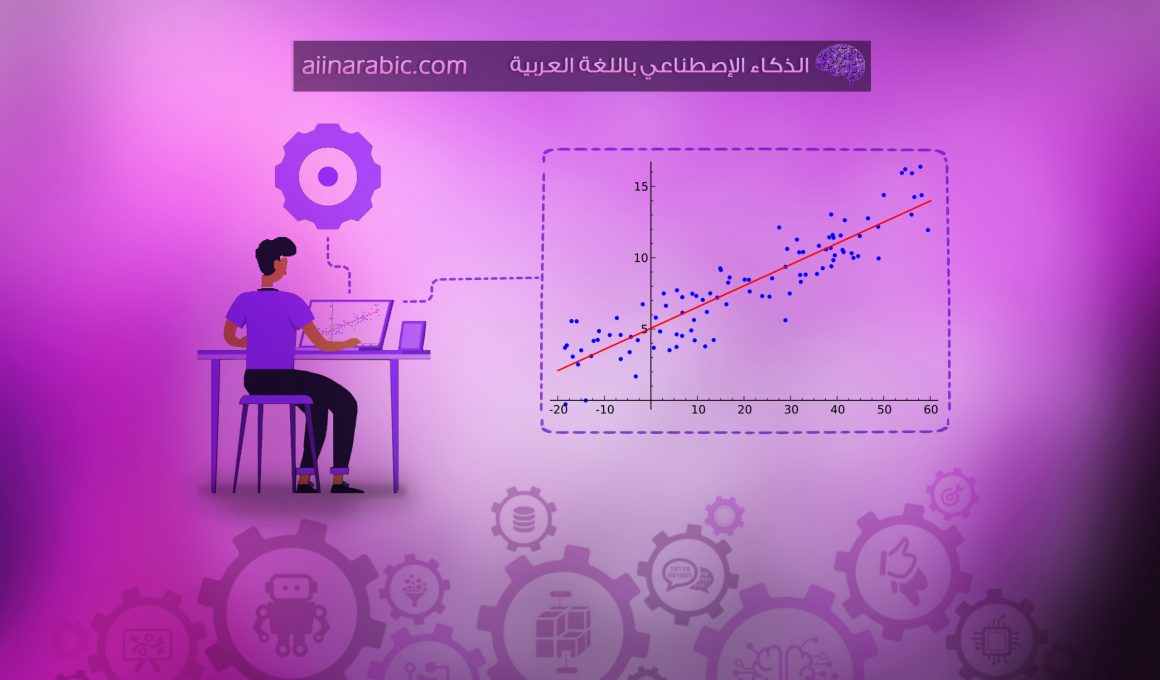
قد يرغب أحد أصحاب المكاتب العقاريّة،  بأن يتنبّأ بسعرِ بيع العقارات بناءً على مواصفاتها، لذا وبشكلٍ بِدائيٍّ سيقوم بتقريبِ سعر كلّ عقار إلى عقارٍ آخر مشابهٍ لمواصفاته،  وقد تكون هناك نسبة خطأ في ذلك التنبّؤ، إذ أنّ العقارين ليسا متطابقين بشكلٍ تامّ، ولكن إن أردنا تمثيل ذلك بشكلٍ رياضيّ أكثر دقّة، حيث يكون سعر العقار تابعاً يحوي متغيراتٍ  تمثّل مواصفات العقار، ومن ثَمّ سيتمّ تحديد خط بيانيّ مناسب يمرّ من ضمن تلك النّقاط النّاتجة من هذا التّابع وتكون نسبة الخطأ _المسافة بين أبعد نقطة والخط البياني_ أقلّ ما يمكن، بهذا تنتج معادلة رياضيّة يستطيع من خلالها صاحب المكتب العقاريّ الحصول على سعر أيّ عقار، وبهذا الشّكل نكون قد استخدمنا أحد تقنيّات التعلّم الآلي الأساسيّة المستخدمة للتنبّؤ ألا وهي تحليل الانحدار …

سنتحدّث في هذه المقالة عن المحاور التّالية:

مفهوم الانحدار

تحليل الانحدار Regression Analysis طريقة إحصائيّة وأسلوب نمذجة تنبؤيّة تدرس العلاقة بين الهدف (المتغيّر التّابع) والمتنبِّئ (المتغيّر أو المتغيّرات المستقلّة)، ويعدّ أداة مهمّة لنمذجة البيانات وتحليلها والتعرُّف على طبيعة العلاقة بين المتغيّرات وقياس تلك العلاقة رقميّاً، وهذا يتطلّب تحديد العوامل المؤثِّرة في ذلك النّموذج وصياغة العلاقة بين هذه العوامل في صورة نموذج قياسيّ يعبّر عنها، وهو شبيه بالتّصنيف Classification إلّا أنّه يتنبّأ بقيم مستمرّة بدلاً من أصنافٍ منفصلة.

أنواع الانحدار

هنالك أنواع مختلفة من تقنيات الانحدار التي تُستخدم في علم البيانات والتعلّم الآلي،  ولكلّ نوع أهميّته الخاصّة في حالات مختلفة ولكن في الأساس تُحلّل جميع تقنيات الانحدار تأثير المتغيّرات المستقلّة على المتغيّرات التّابعة، واختيار تقنيّة الانحدار المناسبة للنّموذج هي المهمّة الأصعب ليس فقط في الانحدار وإنّما في التعلّم الآليّ بشكلٍ عامّ حيث الاختيار الصّحيح يُجنّبنا عناء التّدريب غير المُجدي ونسبة الخطأ الكبيرة، فعلى سبيل المثال: إن كان المتغيّر التّابع مستمراً فالانحدار الخطّيّ هو النّوع الأوّل الذي يجب التّفكير فيه، أمّا إذا كان التّابع مستمراً وكان التّموذج يحتوي على علاقة خطيّة متداخلة،  أو الكثير من المتغيّرات المستقلّة فيمكن تجربة انحدار ريدج أو لاسو، وفي حال استخدام بيانات فئويّة فيمكن استخدام انحدار بواسون، أمّا انحدار المتّجه الدّاعم يستخدم في حال كان النّموذج مزيجاً من الخطّيّ و غير الخطّيّ.

وفيما يلي سنقوم بشرح عدّة أنواع من الانحدارات وفهم طرق استخدامها.

الانحدار الخطّيّ Linear Regression

الانحدار الخطّيّ البسيط Simple Linear Regression

هو أبسط أشكال الانحدار وأكثرها شيوعاً،  ويقوم بتقدير العلاقة التي تربط بين متغيّرين أحدهما المتغيّر التّابع والآخر المتغيّر المستقل،ّ وتكون العلاقة التي تربطهما علاقة خطّيّة، وينتج من هذا النّموذج معادلة خطيّة يمكن استخدامها لتفسير العلاقة بينهما أو لتقدير قيمة المتغير التّابع عند معرفة قيمة المتغير المستقلّ.

وتكون العلاقة الرياضيّة بالشكل التالي:

حيث: Yi= المتغيّر التّابع، Xi= المتغيّر المستقلّ، Ei= الخطأ العشوائيّ، B0= قيمة ثابتة تعبّر عن قيمة المتغيّر التّابع عندما يكون المتغيّر المستقلّ مساوياً للصّفر، B1= هو ميل الخطّ المستقيم الذي يمثّل العلاقة[1].

الانحدار الخطّيّ المتعدّد Multiple Linear Regression

يستخدم الانحدار الخطّيّ المتعدّد في حال كان لدينا متغيّران مستقلّان أو أكثر، حيث يوجد معادلة خطّيّة تربط بين المتغير التّابع وعدّة متغيّرات مستقلّة شريطة أن تكون المتغيّرات غير مرتبطة خطّيّاً، وهو الأكثر فاعلية وواقعيّة من استخدام متغيّر مستقلّ واحد.

وتكون العلاقة الرياضيّة بالشّكل التّالي:

حيث: Yi= المتغيّر التّابع، Xi= المتغيّرات المستقلّة، Ei= الخطأ العشوائيّ، B0= قيمة ثابتة تعبّر عن قيمة المتغيّر التّابع عندما يكون المتغيّر المستقلّ مساوياً للصفر، Bi= هو المعامل المرتبط بالمتغيّر ، n= تمثل عدد المتغيّرات المستقلّة(نجد أنّه عندما n=1 نعود للانحدار الخطّيّ البسيط)[1].

الانحدار اللّا خطّيّ Nonlinear Regression

الانحدار متعدّد الحدود Polynomial Regression

هو أحد أشكال تحليل الانحدار ويتم فيه نمذجة العلاقة بين المتغيّرات المستقلّة والمتغيّرات التّابعة في كثير حدود من الدّرجة n، والانحدار الخطيّ هو في الأساس متعدّد الحدود من الدّرجة الأولى لكن ازدياد درجة الحدود تعطينا الشّكل المنحني الأكثر ملاءمةً للبيانات (كما نعلم الدّرجة الأولى تعبّر عن الخط المستقيم)، ولا يتطّب أن تكون العلاقة بين المتغيّرات المستقلّة والتّابعة خطّية، وهذا أيضاً أحد الاختلافات بين الانحدار الخطّيّ و متعدّد الحدود[2].

وتكون العلاقة الرياضيّة بالشّكل التّالي:

الانحدار اللّوجستيّ Logistic Regression

يتمّ استخدامه في حال كان ناتج المتغيّر التّابع فئوياً، وتكون النّتيجة عبارةً عن احتمال [0,1] بعكس نموذج الانحدار الخطّيّ، حيث يكون النّاتج متراوحاّ بين اللّانهاية السّالبة والموجبة، ويعطي التابع منحنياً على شكل حرف S ويعرف باسم “الوظيفة السّينية”[3].

بفرض:

وتكون علاقته الرّياضيّة بالشّكل التّالي:

  الانحدار التّرتيبيّ Ordinal Regression

هو أسلوب تعلّم آلة يستخدم للتنبّؤ بالمتغيّر التّابع الذي سيكون بترتيبٍ محدّد، وهو وسيطٌ بين الانحدار والتّصنيف يستخدم للتنبّؤ بمتغيّر ترتيبيّ؛ أي توجد قيمته على مقياس عشوائيّ حيث يكون فقط التّرتيب النّسبيّ بين القيم المختلفة مهمّاً[4].

الانحدار الكمّي Quality Regression

يستخدم عندما يكون هناك تباين متزايد في المعادلة، أي كلّما زاد حجم x أصبحت y أكثر تغيّراً، وبذلك يكون الانحدار الخطّيّ غير مفيد لأنّ الخطّ المستقيم يتقارب فقط مع النّقاط في القيم الأولى ومن ثَم يتباعد،  وهنا لا نحتاج لخطٍّ منحنٍ حيث يكفي إنشاء مستقيمين (على أقلّ تقدير) وتُحصر النّقاط بينهما[4].

الانحدار التّدريجيّ Stepwise Regression

يتمّ استخدام هذا النّوع من الانحدار عندما نتعامل مع متغيّرات مستقلّة متعدّدة، ويتبع ثلاثة إجرائيّات:

الأولى _ التّحديد الأماميّ: الذي يتضمن إضافة عوامل مراراً و تكراراً للتحقق من التّحسين، ويتوقف عندما لا يمكن زيادة تحسينات أخرى عند الإضافة.

الثّانية _ التّحديد الخلفيّ: الذي يتضمن إلغاء العوامل كلّ على حدة للوصول لنقطة لا يمكن محو المزيد منها، وتكون تلك العوامل كافيةً لتحليل النّموذج.

الثّالثة _ التّحديد ثنائيّ الاتجاه: وهو مزيج من المنهجين السّابقين، مع كلّ تقدّم يتمّ إضافة متغيّر أو طرحه للوصول إلى العوامل الكافية للنّموذج[4].

انحدار المتّجه الدّاعم Support Vector Regression

هي خوارزميّة انحدار تدعم كلاً من الانحدار الخطّيّ و اللّاخطّيّ، وتقوم على إيجاد دالّة تنتقل من مجال تقريبيّ إلى أرقام ثابتة للنّاتج على أساس عيّنة تدريبيّة وتختلف SVR عن SVM بأنّها تُستخدم للتنبّؤ بمتغيّرات مرتّبة مستمرّة بينما الأخيرة تُستخدم لمتغيّرات فئويّة منفصلة[4][7].

  انحدار المكوّنات الأساسيّة Principal Components Regression

تُستخدم لتحليل المتغيّرات المستقلّة x واختيار مجموعة فرعيّة منها كمتغيّرات أساسيّة للتنبّؤ؛ أي تقوم على تقليلِ عددٍ كبير من المتغيّرات التّوضيحيّة في نموذج الانحدار وصولاً إلى عددٍ صغيرٍ من المكوّنات الأساسيّة، انطلاقاً من أنّ العدد الكبير من المتغيّرات لا يعطي قيمةً أكبر للنّموذج بل يزيد من الأخطاء، تعد PCR و PCA تقنيّات مفيدة لتقليل المتغيّرات عند النّمذجة، وتكون مفيدةً بشكل خاصّ عندما تكون تلك المتغيّرات شديدة الارتباط الخطّيّ[4][8].

انحدار المربّعات الصّغرى الجزئيّة Partial Least Squares Regression

على غرار المكوّنات الأساسيّة تقلّل PLSR من المتغيّرات المستقلّة لاستخراج عدد أقل من المكوّنات للنّموذج؛ أي أنّه إذا قمت بحساب جميع المتغيّرات الممكنة فإنّ النّموذج النّاتج يكون مكافئاً للنّموذج الذي ستحصل عليه باستخدام PLSR، وأيضاً هو مفيد في حال كانت المتغيّرات المستقلّة شديدة الارتباط[5][4].

انحدار كوكس Cox Regression

يُعرف باسم انحدار كوكس لتحليل البقاء، حيث أنّ معاملات كوكس تتعلّق بالمخاطر، يشير المعامل الإيجابيّ إلى تشخيص أسوأ ويشير المعامل السلبي إلى تأثير وقائيّ للمتغيّر الذي يرتبط به، ويفترض أنّ تأثيرات المتغيّرات المتنبِّئة على البقاء ثابتة بمرور الوقت[6][4].     

انحدار البايزي Bayesian Regression

يقوم بصياغة النّموذج باستخدام توزيعات احتماليّة بدلاً من تقديرات نقطيّة، لا يقوم بالعثور على قيمة فرديّة لمعاملات النّموذج بتحديد التّوزيع التّالي لتلك المعاملات، أي أنّه لا يتمّ تدريب نموذج واحد فقط بل مجموعة من النّماذج ويتمّ إعطاؤهم أوزاناً مختلفة وفقاً لصحّة احتمالاتهم[4].

انحدار ريدج Ridge Regression

يساعد في تحليل البيانات ذات الارتباط الشديد مع منع المُلائمة الزَّائدة overfitting للنّموذج، يقلّل هذا النّوع من التباين الكبير في النّموذج الذي تسبّبه العلاقات الخطّيّة عن طرق التّنظيم L2 _حيث L2 تحاول التّقليل من متغيرات التّابع من خلال إضافة قيمةٍ تعبّر عن التّخميد إلى مجموع مربّعات المعاملات_ يعمل الإجراء على التّخلص من الكثير من التباين مع القليل من التّحيّز مما ينتج عنه معاملات انحدار أكثر فائدة[4][9].

انحدار لاسو Lasso Regression

يستخدم أسلوب تنظيم آخر L1 _حيث L1 تحاول التّقليل من متغيرات التّابع من خلال إضافة قيمةٍ تعبّر عن التّخميد إلى القيم المطلقة للمعاملات_ لتبسيط النّموذج أي أنّه مشابهٌ لانحدار ريدج ولكن مع اختيار متغيّر، يتمُّ اختيار المتغيّر الذي يزيد من دقّة التنبّؤ أما في حال كان المتغيّر يزيد من تعقيد النّموذج، تصبح قيمة المعامل المرتبط به أقرب إلى الصفر وهو ما لا يحدث مع انحدار ريدج، وهذا يساعد في تجنب الإفراط في النّموذج[4][9].

انحدار الشّبكة المرنة Elastic Net Regression

هو مزيج من انحدار ريدج و لاسو ويستخدم نمطَيّ التّنظيمregularization وهما L1 و L2 ويُستخدم في SVM للمقاربة[4].

انحدار بواسون Poisson Regression

هو طريقة قياسيّة مستخدمة لنمذجة البيانات بالاعتماد على توزيع بواسون الذي يفترض بشكل أساسيّ المساواة بين المتوسط والتّباين(مربع الانحراف المعياري)، وفي حال كان التّباين أكبر من المتوسّط نلجأ للانحدار السّلبيّ ذي  الحدَّين[4].

الانحدار السّلبيّ ثنائيّ الحد Negative Binomial Regression

هو توزيع بواسون مع المعاملة ’لمدا’ λ (لمدا متغيّر عشوائيّ يتبع توزيع غاما) و’غاما’ γ وهي دالّة احتماليّة مستمرّة  عبارة عن متوسّط أو وقت انتظار متوقّع لحدث عشوائيّ[4].

التّرابط بين تحليل الانحدار وتعلّم الآلة

يكمن أساس التّرابط بينهما من خلال استخراج الحاسوب الخوارزميّة أو نموذج الحلّ المُعبَّر عنه بتابعٍ رياضيّ عندما لانستطيع  كتابة خوارزميّة لتلك المسائل  أو استنتاج المعادلة الرّياضيّة ذات الشّكل الخاصّ المناسب لحلّها، يمكن على سبيل المثال إيجاد علاقة رياضيّة لمعرفة وزن الشّخص من خلال عوامل مؤثّرة بالوزن، حيث يمكن تمثيل ذلك  بشبكة عصبيّة لإيجاد تلك العلاقة، حيث الدّخل عبارة عن المتغيّرات المستقلّة (العوامل المؤثّرة بالوزن)، أما الأوزان المرتبطة بالمداخل تُعبّر عن المعاملات الخاصّة للعوامل، وخرج الشّبكة يعبّر عن خرج التّابع (وزن الشّخص) كما في الشّكل(5).

هُنا يبقى  لدينا اختيار تابع التّفعيل المناسب للشّبكة (أحد أنواع الانحدارات السّابقة) لتتقارب النّتيجة المطلوبة عند تدريب الشبكة، حيث يكون التّعديل فقط على قيم الأوزان من خلال حساب نسبة الخطأ وهذا ما يحدث حرفيّاً في تحليل الانحدار.

تطبيقات تحليل الانحدار

يُستخدم تحليل الانحدار في العديد من المجالات كالاقتصاد والأعمال والأرصاد و الطّب والبيولوجيا والهندسة والفيزياء وعلم النّفس… وغيرها، نستعرض فيما يلي بعض الأمثلة العمليّة:

• التّحليلات التنبّؤيّة: أي التنبّؤ بالفرص والمخاطر المستقبليّة، يعدُّ هذا النّوع من التّحليلات  الأبرز لتحليل الانحدار في مجال الاقتصاد، سوق الأموال (البورصة من خلال التنبّؤ بازدياد قيمة سهم أو نقصانه) وفي مجال سوق الأعمال فقد يتنبّأ بكميّات الطّلب، على سبيل المثال: التنبّؤ بعدد المنتجات التي من المحتمل أن يشتريها المستهلك، ويمكن أن يذهب تحليل الانحدار إلى التنبّؤ بالتّأثير على الإيرادات، على سبيل المثال: يمكننا توقّع عدد المتسوقين الذين سيمرّون أمام لوحة إعلانيّة معيّنة واستخدام هذه البيانات لتقدير الحدّ الأقصى لسعر إعلانٍ ما.
• تصحيح الأخطاء: يساهم تحليل الانحدار في تجنّب الوقوع في القرارات غير المرغوب فيها، على سبيل المثال: قد يعتقد مدير متجر بأنّ تمديد ساعات فتح المتجر سيزيد المبيعات بشكلٍ كبير، لكن قد يشير التّحليل في المقابل أنّه سيؤدّي ذلك إلى ارتفاع نفقات التّشغيل بسبب ساعات العمل الأطول، وبهذا يوفّر تحليل الانحدار دعماً أكبر للقرارات ويمنع الأخطاء المبنيّة على الحدْس.
• التّاريخ: يمكننا باستخدام تحليل الانحدار تقدير عمر الأشياء بناءً على بعض الخصائص المرتبطة بالعمر، على سبيل المثال: تحديد عمر الجماجم الموجودة في المقابر الفرعونية في الأهرامات المصرية، باعتبار المتّغير التّابع هو عمر الجمجمة، والمتغيّرات المستقلّة هي: الحدُّ الأقصى لاتّساع الجمجمة، وطول قاعدة الفكّ للجمجمة، وارتفاع الأنف …وغيرها كما هو الحال في علم الآثار.
• العلوم البيئيّة: يمكن لتحليل الانحدار التنبّؤ بحالة الطّقس كما هو الحال في الأرصاد الجويّة، وفي علم الفلك يستطيع التنبّؤ بحركة الكواكب والنّجوم واحتمالات التّصادم … وغيرها كنسب استهلاك المياه أو نسب التّلوث بسبب أدخنة المصانع …إلخ.

الخُلاصة

تحليل الانحدار هو من التّقنيّات الأساسيّة في علم تعلّم الآلة ، ويعمل على إيجاد العلاقة بين متغيّر تابع ومتغيّر أو عدّة متغيّرات مستقلّة، حيث ينطوي على تحديد أفضل خطّ يمرُّ بين نقاط البيانات الأصليّة ويتمُّ استخدام أنواع مختلفة لتقنيّات الانحدار لملاءمة ذلك الخطّ وتقليل نسبة الخطأ والابتعاد عن الإفراط باستخدام المعاملات.

المراجع

1. regression-analysis
2. polynomial-regression
3. logistic-regression
4. poisson-regression
5. partial-least-squares-regression
6. cox_regression
7. support-vector-regression
8. principal-components-regression
9. ridge-and-lasso-regression